Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-25T05:17:39.067Z Has data issue: false hasContentIssue false
  • English
  • Français

On invariants in grid turbulence at moderate Reynolds numbers

Published online by Cambridge University Press:  06 December 2013

T. Kitamura ,
K. Nagata ,
Y. Sakai ,
A. Sasoh ,
O. Terashima ,
H. Saito  and
T. Harasaki
T. Kitamura
Affiliation:
Department of Mechanical Science and Engineering, Nagoya University, Nagoya, Aichi 464-8603, Japan
K. Nagata*
Affiliation:
Department of Mechanical Science and Engineering, Nagoya University, Nagoya, Aichi 464-8603, Japan
Y. Sakai
Affiliation:
Department of Mechanical Science and Engineering, Nagoya University, Nagoya, Aichi 464-8603, Japan
A. Sasoh
Affiliation:
Department of Aerospace Engineering, Nagoya University, Nagoya, Aichi 464-8603, Japan
O. Terashima
Affiliation:
Department of Mechanical Science and Engineering, Nagoya University, Nagoya, Aichi 464-8603, Japan
H. Saito
Affiliation:
Department of Mechanical Science and Engineering, Nagoya University, Nagoya, Aichi 464-8603, Japan
T. Harasaki
Affiliation:
Department of Aerospace Engineering, Nagoya University, Nagoya, Aichi 464-8603, Japan
*
†Email address for correspondence: nagata@nagoya-u.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

The decay characteristics and invariants of grid turbulence were investigated by means of laboratory experiments conducted in a wind tunnel. A turbulence-generating grid was installed at the entrance of the test section for generating nearly isotropic turbulence. Five grids (square bars of mesh sizes 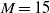$M= 15$, 25 and 50 mm and cylindrical bars of mesh sizes 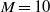$M= 10$ and 25 mm) were used. The solidity of all grids is 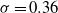$\sigma = 0. 36$. The instantaneous streamwise and vertical (cross-stream) velocities were measured by hot-wire anemometry. The mesh Reynolds numbers were adjusted to 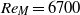$R{e}_{M} = 6700$, 9600, 16 000 and 33 000. The Reynolds numbers based on the Taylor microscale 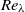$R{e}_{\lambda } $ in the decay region ranged from 27 to 112. In each case, the result shows that the decay exponent of turbulence intensity is close to the theoretical value of 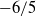${- }6/ 5$ (for the 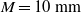$M= 10~\mathrm{mm} $ grid, 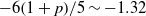${- }6(1+ p)/ 5\sim - 1. 32$) for Saffman turbulence. Here, 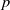$p$ is the power of the dimensionless energy dissipation coefficient, 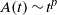$A(t)\sim {t}^{p} $. Furthermore, each case shows that streamwise variations in the integral length scales, ${L}_{uu} $ and 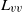${L}_{vv} $, and the Taylor microscale 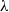$\lambda $ grow according to 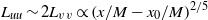${L}_{uu} \sim 2{L}_{vv} \propto {(x/ M- {x}_{0} / M)}^{2/ 5} $ (for the 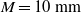$M= 10~\mathrm{mm} $ grid, 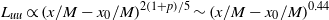${L}_{uu} \propto {(x/ M- {x}_{0} / M)}^{2(1+ p)/ 5} \sim {(x/ M- {x}_{0} / M)}^{0. 44} $) and 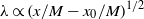$\lambda \propto {(x/ M- {x}_{0} / M)}^{1/ 2} $, respectively, at 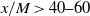$x/ M\gt 40{\unicode{x2013}} 60$ (depending on the experimental conditions, including grid geometry), where $x$ is the streamwise distance from the grid and 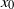${x}_{0} $ is the virtual origin. We demonstrated that in the decay region of grid turbulence, 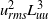${ u}_{\mathit{rms}}^{2} { L}_{uu}^{3} $ and 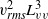${ v}_{\mathit{rms}}^{2} { L}_{vv}^{3} $, which correspond to Saffman’s integral, are constant for all grids and examined 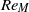$R{e}_{M} $ values. However, 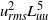${ u}_{\mathit{rms}}^{2} { L}_{uu}^{5} $ and 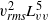${ v}_{\mathit{rms}}^{2} { L}_{vv}^{5} $, which correspond to Loitsianskii’s integral, and 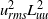${ u}_{\mathit{rms}}^{2} { L}_{uu}^{2} $ and 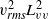${ v}_{\mathit{rms}}^{2} { L}_{vv}^{2} $, which correspond to the complete self-similarity of energy spectrum and 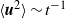$\langle {\boldsymbol{u}}^{2} \rangle \sim {t}^{- 1} $, are not constant. Consequently, we conclude that grid turbulence is a type of Saffman turbulence for the examined 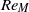$R{e}_{M} $ range of 6700–33 000 (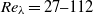$R{e}_{\lambda } = 27{\unicode{x2013}} 112$) regardless of grid geometry.

JFM classification

Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 738 , 10 January 2014 , pp. 378 - 406
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A., Lee, S. K., Djenidi, L., Lavoie, P. & Danaila, L. 2013 Invariants for slightly heated decaying grid turbulence. J. Fluid Mech. 727, 379–406.Google Scholar
Antonia, R. A., Smalley, R. J., Zhou, T., Anselmet, F. & Danaila, L. 2003 Similarity of energy structure functions in decaying homogeneous isotropic turbulence. J. Fluid Mech. 487, 245–269.CrossRefGoogle Scholar
Batchelor, G. K. 1948 Energy decay and self-preserving correlation functions in isotropic turbulence. Q. Appl. Maths. 6, 97–114.CrossRefGoogle Scholar
Batchelor, G. K. 1949 The role of big eddies in homogeneous turbulence. Proc. R. Soc. Lond. A 195, 513–532.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Batchelor, G. K. & Proudman, I. 1956 The large-scale structure of homogeneous turbulence. Phil. Trans. R. Soc. A 248, 369–405.Google Scholar
Batchelor, G. K. & Townsend, A. A. 1948 Decay of turbulence in the final period. Proc. R. Soc. Lond. A 194, 527–543.Google Scholar
Bennett, J. C. & Corrsin, S. 1978 Small Reynolds number nearly isotropic turbulence in a straight duct and a contraction. Phys. Fluids 21, 2129–2140.CrossRefGoogle Scholar
Burattini, P., Lavoie, P., Agrawal, A., Djenidi, L. & Antonia, R. A. 2006 Power law of decaying homogeneous isotropic turbulence at low Reynolds number. Phys. Rev. E 73, 066304.CrossRefGoogle ScholarPubMed
Chasnov, J. R. 1993 Computation of the Loitsyansky integral in decaying isotropic turbulence. Phys. Fluids 5, 2579–2581.CrossRefGoogle Scholar
Comte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotropy of grid-generated turbulence. J. Fluid Mech. 25, 657–682.Google Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Davidson, P. A. 2011 The minimum energy decay rate in quasi-isotropic grid turbulence. Phys. Fluids 23, 085108.Google Scholar
Dryden, H. L. 1943 A review of the statistical theory of turbulence. Q. Appl. Maths. 1, 7–42.Google Scholar
Gad-El-Hak, M. & Corrsin, S. 1974 Measurements of the nearly isotropic turbulence behind a uniform jet grid. J. Fluid Mech. 62, 115–143.CrossRefGoogle Scholar
George, W. K. 1992 The decay of homogeneous isotropic turbulence. Phys. Fluids 4, 1492–1509.CrossRefGoogle Scholar
George, W. K. & Davidson, L 2004 Role of initial conditions in establishing asymptotic flow behaviour. AIAA J. 42, 438–446.Google Scholar
Hinze, J. O. 1959 Turbulence. McGraw-Hill.Google Scholar
Huang, M. J. & Leonard, A. 1994 Power-law decay of homogeneous turbulence at low Reynolds numbers. Phys. Fluids 6, 3765–3775.CrossRefGoogle Scholar
Ishida, T., Davidson, P. A. & Kaneda, Y. 2006 On the decay of isotropic turbulence. J. Fluid Mech. 564, 455–475.Google Scholar
Kaneda, Y., Ishihara, T., Yokokawa, M., Itakura, K. & Uno, A. 2003 Energy dissipation rate and energy spectrum in high resolution direct numerical simulations of turbulence in a periodic box. Phys. Fluids 15, 21–24.Google Scholar
Kang, H. S., Chester, S. & Meneveau, C. 2003 Decaying turbulence in an active-grid-generated flow and comparisons with large-eddy simulation. J. Fluid Mech. 480, 129–160.CrossRefGoogle Scholar
von Kármán, T. & Lin, C. C. 1949 On the concept of similarity in the theory of isotropic turbulence. Rev. Mod. Phys. 21, 516–519.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941 On the degeneration of isotropic turbulence in an incompressible viscous fluid. Dokl. Akad. Nauk SSSR 31, 538–540.Google Scholar
Korneyev, A. I. & Sedov, L. I. 1976 Theory of isotropic turbulence and its comparison with experimental data. Fluid Mech. Sov. Res. 5, 37–47.Google Scholar
Krogstad, P. Å & Davidson, P. A. 2010 Is grid turbulence Saffman turbulence? J. Fluid Mech. 642, 373–394.CrossRefGoogle Scholar
Lavoie, P., Burattini, P., Djenidi, L. & Antonia, R. A. 2005 Effect of initial conditions on decaying grid turbulence at low ${R}_{\lambda } $ . Exp. Fluids 39, 865–874.CrossRefGoogle Scholar
Lavoie, P., Djenidi, L. & Antonia, R. A. 2007 Effects of initial conditions in decaying turbulence generated by passive grids. J. Fluid Mech. 585, 395–420.Google Scholar
Lesieur, M. 2008 Turbulence in Fluids, 4th edn. Springer.Google Scholar
Lesieur, M. & Ossia, S. 2000 3D isotropic turbulence at very high Reynolds numbers: EDQNM study. J. Turbul. 1, 1–25.CrossRefGoogle Scholar
Makita, H. 1991 Realization of a large-scale turbulence field in a small wind tunnel. Fluid Dyn. Res. 8, 53–64.Google Scholar
Mohamed, M. S. & LaRue, J. C. 1990 The decay power law in grid-generated turbulence. J. Fluid Mech. 219, 195–214.Google Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics, vol. II, MIT.Google Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.Google Scholar
Nagata, K., Hunt, J. C. R., Sakai, Y. & Wong, H. 2011 Distorted turbulence and secondary flow near right-angled plates. J. Fluid Mech. 668, 446–479.Google Scholar
Saffman, P. G. 1967 The large-scale structure of homogeneous turbulence. J. Fluid Mech. 27, 581–593.Google Scholar
Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Schedvin, J., Stegen, G. R. & Gibson, C. H. 1974 Universal similarity at high grid Reynolds numbers. J. Fluid Mech. 65, 561–579.CrossRefGoogle Scholar
Speziale, C. G. & Bernard, P. S 1992 The energy decay in self-preserving isotropic turbulence revisited. J. Fluid Mech. 241, 645–667.CrossRefGoogle Scholar
Sreenivasan, K. R. 1984 On the scaling of the turbulence energy dissipation rate. Phys. Fluids 27, 1048–1051.CrossRefGoogle Scholar
Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7, 2778–2784.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.CrossRefGoogle Scholar
Taylor, G. I. 1935 Statistical theory of turbulence. Proc. Trans. R. Soc. A 151, 421–444.Google Scholar