Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-26T11:09:26.745Z Has data issue: false hasContentIssue false
  • English
  • Français

On high-order perturbation expansion for the study of long–short wave interactions

Published online by Cambridge University Press:  11 May 2018

Yulin Pan ,
Yuming Liu Open the ORCID record for Yuming Liu [Opens in a new window]  and
Dick K. P. Yue Open the ORCID record for Dick K. P. Yue [Opens in a new window]
Yulin Pan
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Yuming Liu
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Dick K. P. Yue*
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: yue@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In high-order analysis and simulation of long–short surface wave interaction using mode decomposition, ‘divergent’ terms of the form 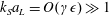$k_{S}a_{L}=O(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D716})\gg 1$ appear in the high-order expansions, where 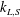$k_{L,S}$ , 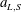$a_{L,S}$ are respectively the long, short modal wavenumbers and amplitudes, with 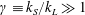$\unicode[STIX]{x1D6FE}\equiv k_{S}/k_{L}\gg 1$ and 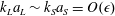$k_{L}a_{L}\sim k_{S}a_{S}=O(\unicode[STIX]{x1D716})$ finite. We address the effect of these terms on the numerical scheme, showing numerical cancellation at all orders 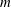$m$ ; but increasing ill-conditioning of the numerics with 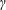$\unicode[STIX]{x1D6FE}$ and $m$ , which we quantify. In the context of mode decomposition, we show theoretical exact cancellation of the divergent terms up to 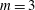$m=3$ , extending the existing result of Brueckner & West (J. Fluid Mech., vol. 196, 1988, pp. 585–592) and supporting the conjecture that this is obtained for all orders 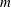$m$ . We show the latter by developing a theoretical proof for any 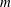$m$ using a Dirichlet–Neumann operator and mathematical induction. The implication of the theoretical proof on the numerical simulation of long–short wave interaction is discussed.

JFM classification

Mathematical Foundations: Computational methods Mathematical Foundations: Mathematical Foundations Waves/Free-surface Flows: Waves/Free-surface Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 846 , 10 July 2018 , pp. 902 - 915
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Banner, M. L. & Young, I. R. 1994 Modeling spectral dissipation in the evolution of wind waves. Part I. Assessment of existing model performance. J. Phys. Oceanogr. 24 (7), 1550–1571.2.0.CO;2>CrossRefGoogle Scholar
Brueckner, K. A. & West, B. J. 1988 Vindication of mode-coupled descriptions of multiple-scale water wave fields. J. Fluid Mech. 196, 585–592.CrossRefGoogle Scholar
Bruno, O. P. & Reitich, F. 1993 Numerical solution of diffraction problems: a method of variation of boundaries. J. Opt. Soc. Am. A 10 (6), 1168–1175.CrossRefGoogle Scholar
Craig, W. & Sulem, C. 1993 Numerical simulation of gravity waves. J. Comput. Phys. 108 (1), 73–83.CrossRefGoogle Scholar
Dommermuth, D. G. 1994 Efficient simulation of short and long wave interactions with applications to capillary waves. Trans. ASME J. Fluids Engng 116 (1), 77–82.Google Scholar
Dommermuth, D. G. & Yue, D. K. P. 1987 High-order spectral method for the study of nonlinear gravity waves. J. Fluid Mech. 184 (1), 267–288.CrossRefGoogle Scholar
Holliday, D. 1977 On nonlinear interactions in a spectrum of inviscid gravity–capillary surface waves. J. Fluid Mech. 83 (4), 737–749.Google Scholar
Lenain, L. & Melville, W. K. 2017 Evidence of sea-state dependence of aerosol concentration in the marine atmospheric boundary layer. J. Phys. Oceanogr. 47 (1), 69–84.Google Scholar
Longuet-Higgins, M. S. 1987 The propagation of short surface waves on longer gravity waves. J. Fluid Mech. 177, 293–306.CrossRefGoogle Scholar
Longuet-Higgins, M. S. & Stewart, R. W. 1960 Changes in the form of short gravity waves on long waves and tidal currents. J. Fluid Mech. 8 (4), 565–583.Google Scholar
Miao, S. & Liu, Y. 2015 Wave pattern in the wake of an arbitrary moving surface pressure disturbance. Phys. Fluids 27 (12), 122102.Google Scholar
Milder, D. M. 1990 The effects of truncation on surface-wave Hamiltonians. J. Fluid Mech. 217, 249–262.Google Scholar
Naciri, M. & Mei, C. 1992 Evolution of a short surface wave on a very long surface wave of finite amplitude. J. Fluid Mech. 235, 415–452.Google Scholar
Nicholls, D. P. 2007 Boundary perturbation methods for water waves. GAMM-Mitteilungen 30 (1), 44–74.CrossRefGoogle Scholar
Nicholls, D. P. 2009 Spectral data for travelling water waves: singularities and stability. J. Fluid Mech. 624, 339–360.Google Scholar
Nicholls, D. P. & Reitich, F. 2001 Stability of high-order perturbative methods for the computation of Dirichlet–Neumann operators. J. Comput. Phys. 170 (1), 276–298.CrossRefGoogle Scholar
Ölmez, H. S. & Milgram, J. H. 1995 Numerical methods for nonlinear interactions between water waves. J. Comput. Phys. 118 (1), 62–72.Google Scholar
Pan, Y.2016 Understanding of weak turbulence of capillary waves. PhD thesis, Massachusetts Institute of Technology.Google Scholar
Pan, Y. & Yue, D. K. P. 2014 Direct numerical investigation of turbulence of capillary waves. Phys. Rev. Lett. 113 (9), 094501.CrossRefGoogle ScholarPubMed
Pan, Y. & Yue, D. K. P. 2015 Decaying capillary wave turbulence under broad-scale dissipation. J. Fluid Mech. 780, R1.Google Scholar
Qi, Y., Wu, G., Liu, Y., Kim, M.-H. & Yue, D. K. P. 2018 Nonlinear phase-resolved reconstruction of irregular water waves. J. Fluid Mech. 838, 544–572.Google Scholar
Watson, K. M. & West, B. J. 1975 A transport-equation description of nonlinear ocean surface wave interactions. J. Fluid Mech. 70 (4), 815–826.Google Scholar
West, B. J., Brueckner, K. A., Janda, R. S., Milder, D. M. & Milton, R. L. 1987 A new numerical method for surface hydrodynamics. J. Geophys. Res. 92 (C11), 11803–11811.CrossRefGoogle Scholar
Xiao, W., Liu, Y., Wu, G. & Yue, D. K. P. 2013 Rogue wave occurrence and dynamics by direct simulations of nonlinear wave-field evolution. J. Fluid Mech. 720, 357–392.Google Scholar
Zakharov, V. E. 1968 Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9 (2), 190–194.Google Scholar
Zhang, J., Hong, K. & Yue, D. K. P. 1993 Effects of wavelength ratio on wave modelling. J. Fluid Mech. 248, 107–127.CrossRefGoogle Scholar
Zhang, J. & Melville, W. K. 1990 Evolution of weakly nonlinear short waves riding on long gravity waves. J. Fluid Mech. 214 (1), 321–346.CrossRefGoogle Scholar