Hostname: page-component-848d4c4894-sjtt6 Total loading time: 0 Render date: 2024-07-02T07:49:14.508Z Has data issue: false hasContentIssue false
  • English
  • Français

On grid-generated turbulence in the near- and far field regions

Published online by Cambridge University Press:  24 July 2014

Juan C. Isaza ,
Ricardo Salazar  and
Zellman Warhaft
Juan C. Isaza*
Affiliation:
Department of Mechanical Engineering, Universidad EAFIT, Medellin, Colombia
Ricardo Salazar
Affiliation:
Department of Mechanical Engineering, Universidad EAFIT, Medellin, Colombia
Zellman Warhaft
Affiliation:
Department of Aerospace and Mechanical Engineering, Cornell University, Ithaca, NY, USA
*
†Email address for correspondence: jisaza1@eafit.edu.co
Get access Rights & Permissions [Opens in a new window]

Abstract

Using a conventional bi-planar turbulence-generating grid, we confirm the recent findings (Valente & Vassilicos, Phys. Rev. Lett., vol. 108, 2012, art. 214503) that show there is a turbulence decay region close to the generating grid that departs from the ‘classical’ turbulence decay (Comte-Bellot & Corrsin, J. Fluid Mech., vol. 25, 1966, pp. 657–682). In this ‘near-field’ region, the turbulence energy decays more rapidly than in the far-field and it exhibits unusual scaling properties. Based on the velocity decay laws, we show that for our conventional grid, the near-field extends from 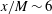$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}x/M \sim 6$ to 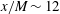$x/M \sim 12$ where $x$ is the downstream distance from the grid and 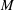$M$ is the mesh size. This corresponds to 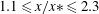$1.1 \le x/x* \le 2.3$ where 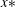$x*$ is the wake interaction length scale (Mazellier & Vassilicos, Phys. Fluids, vol. 22, 2010, art. 075101). However, other statistics (velocity derivatives and length-scale ratios) indicate that the extent of the initial period depends on the grid mesh Reynolds number, 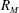$R_M$, extending further for higher values of 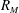$R_M$. In the near-field the turbulence approaches isotropy both at the large and small scales but there still is inhomogeneity in the derivative statistics. The derivative skewness also departs from values observed at comparable Reynolds numbers in the far-field decay region, and in other turbulent flows at comparable Reynolds numbers. Two values of 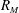$R_M$ were studied: 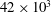$42 \times 10^3$ and 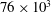$76 \times 10^3$.

JFM classification

Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 753 , 25 August 2014 , pp. 402 - 426
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ayyalasomayajula, S. & Warhaft, Z. 2006 Nonlinear interactions in strained axisymmetric high-Reynolds-number turbulence. J. Fluid Mech. 566, 273–307.CrossRefGoogle Scholar
Browne, L., Antonia, R. & Chua, L. 1989 Calibration of X-probes for turbulent flow measurements. Exp. Fluids 7, 201–208.CrossRefGoogle Scholar
Champagne, F. H., Harris, V. G. & Corrsin, S. 1970 Experiments on nearly homogeneous turbulent shear flow. J. Fluid Mech. 41 (01), 81–139.CrossRefGoogle Scholar
Comte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotropy of grid-generated turbulence. J. Fluid Mech. 25 (04), 657–682.Google Scholar
Comte-Bellot, G. & Corrsin, S. 1971 Simple Eulerian time correlation of full- and narrow-band velocity signals in grid-generated turbulence. J. Fluid Mech. 48 (02), 273–337.Google Scholar
Efron, B. & Tibshirani, R. J. 1994 An Introduction to the Bootstrap. Chapman and Hall.CrossRefGoogle Scholar
Ertunc, O., Ozyilmaz, N., Lienhart, H., Durst, F. & Beronov, K. 2010 Homogeneity of turbulence generated by static-grid structures. J. Fluid Mech. 654, 473–500.Google Scholar
Frisch, U. 1995 Turbulence. The Legacy of A.N. Kolmogorov. Cambridge University Press.Google Scholar
Gylfason, A., Aayyalasomayajula, S. & Warhaft, Z. 2004 Intermittency, pressure and acceleration statistics from hot-wire measurements in wind-tunnel turbulence. J. Fluid Mech. 501, 213–229.Google Scholar
Hearst, R. J. & Lavoie, P. 2014 Decay of turbulence generated by a square-fractal-element grid. J. Fluid Mech. 741, 567–584.Google Scholar
Isaza, J. C., Warhaft, Z. & Collins, L. R. 2009 Experimental investigation of the large-scale velocity statistics in homogeneous turbulent shear flow. Phys. Fluids 21 (6), 065105.CrossRefGoogle Scholar
Jayesh,   & Warhaft, Z. 1992 Probability distribution, conditional dissipation, and transport of passive temperature fluctuations in grid-generated turbulence. Phys. Fluids 4 (10), 2292–2307.Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds. C. R. Acad. Sci. U.R.S.S. 30, 301.Google Scholar
Krogstad, P.-A. & Davidson, P. A. 2011 Freely decaying, homogeneous turbulence generated by multi-scale grids. J. Fluid Mech. 680, 417–434.CrossRefGoogle Scholar
Krogstad, P.-A. & Davidson, P. A. 2012 Near-field investigation of turbulence produced by multi-scale grids. Phys. Fluids 24 (3), 035103.Google Scholar
Makita, H. 1991 Realization of a large-scale turbulence field in a small wind tunnel. Fluid Dyn. Res. 8, 54–64.Google Scholar
Mazellier, N. & Vassilicos, J. C. 2010 Turbulence without Richardson–Kolmogorov cascade. Phys. Fluids 22 (7), 075101.CrossRefGoogle Scholar
Mohamed, M. S. & Larue, J. C. 1990 The decay power law in grid-generated turbulence. J. Fluid Mech. 219, 195–214.CrossRefGoogle Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.Google Scholar
Mydlarski, L. & Warhaft, Z. 1998 Three-point statistics and the anisotropy of a turbulent passive scalar. Phys. Fluids 10 (11), 2885–2894.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Queiros-Conde, D. & Vassilicos, J. C. 2001 Intermittency in Turbulent Flows and Other Dynamical Systems. Cambridge University Press.Google Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.Google Scholar
Siggia, E. D. 1981 Numerical study of small-scale intermittency in three-dimensional turbulence. J. Fluid Mech. 107, 375–406.Google Scholar
Simmons, L. F. G. & Salter, C. 1934 Experimental investigation and analysis of the velocity variations in turbulent flow. Proc. R. Soc. Lond. A 145 (854), 212–234.Google Scholar
Sirivat, A. & Warhaft, Z. 1983 The effect of a passive cross-stream temperature gradient on the evolution of temperature variance and heat flux in grid turbulence. J. Fluid Mech. 128, 323–346.CrossRefGoogle Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29 (1), 435–472.Google Scholar
Tavoularis, S., Bennett, J. C. & Corrsin, S. 1978 Velocity-derivative skewness in small Reynolds number, nearly isotropic turbulence. J. Fluid Mech. 88 (01), 63–69.CrossRefGoogle Scholar
Taylor, G. I. 1935 Statistical theory of turbulence. Proc. R. Soc. Lond. Ser. A 151 (873), 421–444.CrossRefGoogle Scholar
Valente, P. C. & Vassilicos, J. C. 2011 The decay of turbulence generated by a class of multiscale grids. J. Fluid Mech. 687, 300–340.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2012 Universal dissipation scaling for nonequilibrium turbulence. Phys. Rev. Lett. 108, 214503.CrossRefGoogle ScholarPubMed
Valente, P. C. & Vassilicos, J. C. 2014 The non-equilibrium region of grid-generated decaying turbulence. J. Fluid Mech. 744, 5–37.CrossRefGoogle Scholar
Voth, G. A., Satyanarayan, K. & Bodenschatz, E. 1998 Lagrangian acceleration measurements at large Reynolds numbers. Phys. Fluids 10 (9), 2268–2280.Google Scholar
Wyngaard, J. C. & Tennekes, H. 1970 Measurements of the small-scale structure of turbulence at moderate Reynolds numbers. Phys. Fluids 13 (8), 1962–1969.Google Scholar
Yoon, K. & Warhaft, Z. 1990 The evolution of grid-generated turbulence under conditions of stable thermal stratification. J. Fluid Mech. 215, 601–638.CrossRefGoogle Scholar