Article contents
Numerical simulation of jets generated by a sphere moving vertically in a stratified fluid
Published online by Cambridge University Press: 22 January 2015
Abstract
The flow past a sphere moving vertically at constant speeds in a salt-stratified fluid is investigated numerically at moderate Reynolds numbers 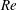 $\mathit{Re}$. Time development of the flow shows that the violation of density conservation is the key process for the generation of the buoyant jet observed in the experiments. For example, if the sphere moves downward, isopycnal surfaces are simply deformed and dragged down by the sphere while the density is conserved along the flow. (The flow pattern is inverted if the sphere moves upward. Some explanations are given in the introduction.) Then, the flow will never become steady. As density diffusion becomes effective around the sphere surface and generates a horizontal hole in the isopycnal surface, fluid with non-conserved density is detached from the isopycnal surface and moves upward to generate a buoyant jet. These processes will constitute a steady state near the sphere. With lengths scaled by the sphere diameter and velocities by the downward sphere velocity, the duration of density conservation at the rear/upper stagnation point, or the maximum distance that the isopycnal surface is dragged downward, is proportional to the Froude number
$\mathit{Re}$. Time development of the flow shows that the violation of density conservation is the key process for the generation of the buoyant jet observed in the experiments. For example, if the sphere moves downward, isopycnal surfaces are simply deformed and dragged down by the sphere while the density is conserved along the flow. (The flow pattern is inverted if the sphere moves upward. Some explanations are given in the introduction.) Then, the flow will never become steady. As density diffusion becomes effective around the sphere surface and generates a horizontal hole in the isopycnal surface, fluid with non-conserved density is detached from the isopycnal surface and moves upward to generate a buoyant jet. These processes will constitute a steady state near the sphere. With lengths scaled by the sphere diameter and velocities by the downward sphere velocity, the duration of density conservation at the rear/upper stagnation point, or the maximum distance that the isopycnal surface is dragged downward, is proportional to the Froude number 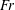 $\mathit{Fr}$, and estimated well by
$\mathit{Fr}$, and estimated well by 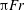 ${\rm\pi}\mathit{Fr}$ for
${\rm\pi}\mathit{Fr}$ for  $\mathit{Fr}\gtrsim 1$ and
$\mathit{Fr}\gtrsim 1$ and 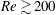 $\mathit{Re}\gtrsim 200$, corresponding to a constant potential energy. The radius of a jet defined by the density and velocity distributions, which would have correlations with the density and velocity boundary layers on the sphere, is estimated well by
$\mathit{Re}\gtrsim 200$, corresponding to a constant potential energy. The radius of a jet defined by the density and velocity distributions, which would have correlations with the density and velocity boundary layers on the sphere, is estimated well by 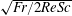 $\sqrt{\mathit{Fr }/2\mathit{Re }\mathit{ Sc}}$ and
$\sqrt{\mathit{Fr }/2\mathit{Re }\mathit{ Sc}}$ and 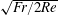 $\sqrt{\mathit{Fr }/2\mathit{Re}}$ respectively for
$\sqrt{\mathit{Fr }/2\mathit{Re}}$ respectively for 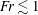 $\mathit{Fr}\lesssim 1$, where
$\mathit{Fr}\lesssim 1$, where 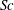 $\mathit{Sc}$ is the Schmidt number. Numerical results agree well with the previous experiments, and the origin of the conspicuous bell-shaped structure observed by the shadowgraph method is identified as an internal wave.
$\mathit{Sc}$ is the Schmidt number. Numerical results agree well with the previous experiments, and the origin of the conspicuous bell-shaped structure observed by the shadowgraph method is identified as an internal wave.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 20
- Cited by





