Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-24T05:09:24.679Z Has data issue: false hasContentIssue false
  • English
  • Français

Normal stress differences in suspensions of rigid fibres

Published online by Cambridge University Press:  09 October 2014

Braden Snook ,
Levi M. Davidson ,
Jason E. Butler ,
Olivier Pouliquen  and
Élisabeth Guazzelli
Braden Snook
Affiliation:
Department of Chemical Engineering, University of Florida, Gainesville, FL 32611, USA Aix-Marseille Université, CNRS, IUSTI UMR 7343, 13453 Marseille, France
Levi M. Davidson
Affiliation:
Department of Chemical Engineering, University of Florida, Gainesville, FL 32611, USA
Jason E. Butler*
Affiliation:
Department of Chemical Engineering, University of Florida, Gainesville, FL 32611, USA
Olivier Pouliquen
Affiliation:
Aix-Marseille Université, CNRS, IUSTI UMR 7343, 13453 Marseille, France
Élisabeth Guazzelli
Affiliation:
Aix-Marseille Université, CNRS, IUSTI UMR 7343, 13453 Marseille, France
*
†Email address for correspondence: butler@che.ufl.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

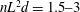Measurements of normal stress differences are reported for suspensions of rigid, non-Brownian fibres for concentrations of $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}nL^2d=1.5\text {--}3$ and aspect ratios of 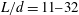$L/d=11\text {--}32$, where $n$ is the number of fibres per unit volume, 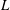$L$ is the fibre length and 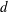$d$ is the diameter. The first and second normal stress differences are determined experimentally from measuring the deformation in the free surface in a tilted trough and in a Weissenberg rheometer. Simulations are performed as well, and the hydrodynamic and contact contributions to the normal stresses are calculated. The experiments and simulations indicate that the second normal stress difference is negative and that its magnitude increases as the concentration is raised and the aspect ratio is lowered. The first normal stress difference is positive and its magnitude is approximately twice that of the second normal stress difference. Simulation results indicate that, for the concentrations and aspect ratios studied, contact forces between fibres form the dominant contribution to the normal stress differences.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Low-Reynolds-number flows: Slender-body theory Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 758 , 10 November 2014 , pp. 486 - 507
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1970 Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech. 44, 419–440.CrossRefGoogle Scholar
Batchelor, G. K. 1971 The stress generated in a non-dilute suspension of elongated particles by pure straining motion. J. Fluid Mech. 46, 813–829.CrossRefGoogle Scholar
Batchelor, G. K. & Green, J. T. 1972 The determination of the bulk stress in a suspension of spherical particles to order $c^2$ . J. Fluid Mech. 56, 401–427.CrossRefGoogle Scholar
Beavers, G. S. & Joseph, D. D. 1975 The rotating-rod viscometer. J. Fluid Mech. 69, 475–512.CrossRefGoogle Scholar
Boyer, F., Pouliquen, O. & Guazzelli, E. 2011 Dense suspensions in rotating-rod flows: normal stresses and particle migration. J. Fluid Mech. 686, 5–25.CrossRefGoogle Scholar
Bretherton, F. P. 1962 The motion of rigid particles in a shear flow at low Reynolds number. J. Fluid Mech. 14, 284–304.CrossRefGoogle Scholar
Couturier, É., Boyer, F., Pouliquen, O. & Guazzelli, É. 2011 Suspensions in a tilted trough: second normal stress difference. J. Fluid Mech. 686, 26–39.CrossRefGoogle Scholar
Cox, R. G. 1970 The motion of long slender bodies in a viscous fluid. Part 1. General theory. J. Fluid Mech. 44, 791–810.CrossRefGoogle Scholar
Dai, S.-C., Bertevas, E., Qi, F. & Tanner, R. I. 2013 Viscometric functions for noncolloidal sphere suspensions with Newtonian matrices. J. Rheol. 57, 493–510.CrossRefGoogle Scholar
Dbouk, T., Lobry, L. & Lemaire, E. 2013 Normal stresses in concentrated non-Brownian suspensions. J. Fluid Mech. 715, 239–272.CrossRefGoogle Scholar
Dinh, S. M. & Armstrong, C. R. 1984 A rheological equation of state for semiconcentrated fiber suspensions. J. Rheol. 28, 207–227.CrossRefGoogle Scholar
Einstein, A. 1905 Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. (Berlin) (4) 17, 549–560; English translation by A. D. Cowper reprinted in 1956 in Investigations on the Theory of Brownian Movement, Dover Publications.CrossRefGoogle Scholar
Forgacs, O. L. & Mason, S. G. 1959 Particle motions in sheared suspensions. Part 9. Spin and deformation of thread-like particles. J. Colloid Interface Sci. 14, 457–472.CrossRefGoogle Scholar
Franceschini, F., Filippidi, E., Guazelli, É. & Pine, D. J. 2011 Transverse alignment of fibers in a periodically sheared suspension: an absorbing phase transition with a slowly-varying control parameter. Phys. Rev. Lett. 107, 250603.CrossRefGoogle Scholar
Goto, S., Nagazono, H. & Kato, H. 1986 The flow behavior of fiber suspensions in Newtonian fluids and polymer solutions. I. Mechanical properties. Rheol. Acta 25, 119–129.CrossRefGoogle Scholar
Hinch, E. J. 2011 The measurement of suspension rheology. J. Fluid Mech. 686, 1–4.CrossRefGoogle Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Keshtkar, M., Heuzey, M. C. & Carreau, P. J. 2009 Rheological behavior of fiber-filled model suspensions: effect of fiber flexibility. J. Rheol. 53, 631–650.CrossRefGoogle Scholar
Kitano, T. & Kataoka, T. 1981 The rheology of suspension of vinyl on fibers in polymer liquids. I. Suspensions in silicone oil. Rheol. Acta 20, 390–402.CrossRefGoogle Scholar
Kuo, Y. & Tanner, R. I. 1974 On the use of open-channel flows to measure the second normal stress difference. Rheol. Acta 13, 443–456.CrossRefGoogle Scholar
Mackaplow, M. B. & Shaqfeh, E. S. G. 1996 A numerical study of the rheological properties of suspensions of rigid, non-Brownian fibres. J. Fluid Mech. 329, 155–186.CrossRefGoogle Scholar
Mason, S. G. & Manley, R. J. 1956 Particle motions in sheared suspensions: orientation and interactions of rigid rods. Proc. R. Soc. Lond. A 238, 117–131.Google Scholar
Petrich, M. P., Koch, D. L. & Cohen, C. 2000 An experimental determination of the stress microstructure relationship in semi-concentrated fiber suspensions. J. Non-Newtonian Fluid Mech. 95, 101–133.CrossRefGoogle Scholar
Petrie, C. J. S. 1999 The rheology of fibre suspensions. J. Non-Newtonian Fluid Mech. 87, 369–402.CrossRefGoogle Scholar
Sepehr, M., Carreau, P. J., Moan, M. & Ausias, G. 2004 Rheological properties of short fiber model suspensions. J. Rheol. 48, 1023–1048.CrossRefGoogle Scholar
Shaqfeh, E. S. G. & Fredrickson, G. F. 1990 The hydrodynamic stress in a suspension of rods. Phys. Fluids 2, 7–24.CrossRefGoogle Scholar
Sierou, A. & Brady, J. F. 2002 Rheology and microstructure in concentrated non-colloidal suspensions. J. Rheol. 46, 1031–1056.CrossRefGoogle Scholar
Singh, A. & Nott, P. R. 2000 Normal stresses and microstructure in bounded sheared suspensions via Stokesian Dynamics simulations. J. Fluid Mech. 412, 279–301.CrossRefGoogle Scholar
Singh, A. & Nott, P. R. 2003 Experimental measurements of the normal stresses in sheared Stokesian suspensions. J. Fluid Mech. 490, 293–320.CrossRefGoogle Scholar
Snook, B., Guazzelli, É. & Butler, J. E. 2012 Vorticity alignment of rigid fibers in oscillatory shear flow: role of confinement. Phys. Fluids 24, 121702.CrossRefGoogle Scholar
Stickel, J. J. & Powell, R. L. 2005 Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 37, 129–149.CrossRefGoogle Scholar
Stover, C. A., Koch, D. L. & Cohen, C. 1992 Observations of fibre orientation in simple shear flow of semi-dilute suspensions. J. Fluid Mech. 238, 277–296.CrossRefGoogle Scholar
Sundararajakumar, R. R. & Koch, D. L. 1997 Structure and properties of sheared fiber suspensions with mechanical contacts. J. Non-Newtonian Fluid Mech. 73 (3), 205–239.CrossRefGoogle Scholar
Tanner, R. I. 1970 Some methods for estimating the normal stress functions in viscometric flows. Trans. Soc. Rheol. 14 (4), 483–507.CrossRefGoogle Scholar
Trevelyan, B. J. & Mason, S. G. 1951 Particle motions in sheared suspensions. I. Rotations. J. Colloid Sci. 6, 354–367.CrossRefGoogle Scholar
Wineman, A. & Pipkin, A. 1966 Slow viscoelastic flow in tilted troughs. Acta Mechanica 2, 104–115.CrossRefGoogle Scholar
Zarraga, I. E., Hill, D. A. & Leighton, D. T. 2000 The characterization of the total stress of concentrated suspensions of noncolloidal spheres in Newtonian fluids. J. Rheol. 44, 185–220.CrossRefGoogle Scholar