Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-26T23:31:31.560Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear stability of gravitationally unstable, transient, diffusive boundary layers in porous media

Published online by Cambridge University Press:  19 March 2014

N. Tilton  and
A. Riaz
N. Tilton
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
A. Riaz*
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
*
†Email address for correspondence: ariaz@umd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The linear stability of transient diffusive boundary layers in porous media has been studied extensively for its applications to carbon dioxide sequestration. The onset of nonlinear convection, however, remains understudied because the transient base state invalidates the traditional stability methods that are used for autonomous systems. 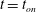We demonstrate that the onset time of nonlinear convection, $t=t_{\mathit{on}}$, can be determined from an expansion that is two orders of magnitude faster than a direct numerical simulation. Using the expansion, we explore the sensitivity of 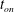$t_{\mathit{on}}$ to the initial perturbation magnitude and wavelength, as well as the initial time at which a perturbation is initiated. We find that there is an optimal initial time and wavelength that minimize 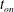$t_{\mathit{on}}$, and we obtain analytical relationships for these parameters in terms of aquifer properties and initial perturbation magnitude. This importance of the initial perturbation time and magnitude is often overlooked in previous studies. To investigate perturbation evolution at late-times, 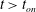$t>t_{\mathit{on}}$, we perform direct numerical simulations that reveal two unique features of transient diffusive boundary layers. First, when a boundary layer is perturbed with a single horizontal Fourier mode, nonlinear mechanisms generate a zero-wavenumber response whose magnitude eventually surpasses that of the fundamental mode. Second, when a boundary layer is simultaneously perturbed with many Fourier modes, the late-time perturbation magnitude is concentrated in the zero-wavenumber mode, and there is no clearly dominant, non-zero, wavenumber. These unique results are further interpreted by comparison with direct numerical simulations of Rayleigh–Bénard convection.

JFM classification

Convection: Buoyancy-driven instability Interfacial Flows (free surface): Fingering instability Instability: Nonlinear instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 745 , 25 April 2014 , pp. 251 - 278
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ben, Y., Demekhin, E. A. & Chang, H.-C. 2002 A spectral theory for small-amplitude miscible fingering. Phys. Fluids 14, 999–1010.Google Scholar
Blair, L. M. & Quinn, J. A. 1969 The onset of convection in a fluid layer with time-dependent density gradients. J. Fluid Mech. 36, 385–400.Google Scholar
Breugem, W. P. & Boersma, B. J. 2005 Direct numerical simulations of turbulent flow over a permeable wall using a direct and a continuum approach. Phys. Fluids 17, 025103.Google Scholar
Caltagirone, J. P. 1980 Stability of a saturated porous layer subject to a sudden rise in surface temperature: comparison between linear and energy methods. Q. J. Mech. Appl. Maths. 33, 47–58.CrossRefGoogle Scholar
Camporeale, C., Mantelli, E. & Manes, C. 2013 Interplay among unstable modes in films over permeable walls. J. Fluid Mech. 719, 527–550.CrossRefGoogle Scholar
Daniel, D., Tilton, N. & Riaz, A. 2013 Optimal perturbations of gravitationally unstable, transient boundary layers in porous media. J. Fluid Mech. 727, 456–487.Google Scholar
Doumenc, F., Boeck, T., Guerrier, B. & Rossi, M. 2010 Transient Rayleigh–Bénard–Marangoni convection due to evaporation: a linear non-normal stability analysis. J. Fluid Mech. 648, 521–539.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Elenius, M. T., Nordbotten, J. M. & Kalisch, H. 2012 Effects of capillary transition on the stability of a diffusive boundary layer. IMA J. Appl. Maths. 77, 771–787.Google Scholar
Ennis-King, J. & Paterson, L. 2003 Role of convective mixing in the long-term storage of carbon dioxide in deep saline formations. SPE 10 (3), 349–356.Google Scholar
Foster, T. D. 1965 Stability of a homogeneous fluid cooled uniformly from above. Phys. Fluids 8, 1249–1257.Google Scholar
Godreche, C. & Manneville, P. 1998 Hydrodynamics and Nonlinear Instabilities. Cambridge Univeristy Press.Google Scholar
Goldstein, A. W.1959 Stability of a horizontal fluid layer with unsteady heating from below and time-dependent body force. Tech. Rep. R-4. NASA.Google Scholar
Green, L. L. & Foster, T. D. 1975 Secondary convection in a Hele Shaw cell. J. Fluid Mech. 71, 675–687.CrossRefGoogle Scholar
Gresho, P. M. & Sani, R. L. 1971 The stability of a fluid layer subjected to a step change in temperature: transient vs. frozen time analyses. Int. J. Heat Mass Transfer 14, 207–221.Google Scholar
Hassanzadeh, H., Pooladi-Darvish, M. & Keith, D. W. 2006 Stability of a fluid in a horizontal saturated porous layer: effect of non-linear concentration profile, initial, and boundary conditions. Trans. Porous Med. 65, 193–211.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2013 Convective shutdown in a porous medium at high Rayleigh number. J. Fluid Mech. 719, 551–586.Google Scholar
Hirata, S. C., Goyeau, B. & Gobin, D. 2007 Stability of natural convection in superposed fluid and porous layers: influence of the interfacial jump boundary condition. Phys. Fluids 19, 058102.Google Scholar
James, D. F. & Davis, A. M. J. 2001 Flow at the interface of a model fibrous porous medium. J. Fluid Mech. 426, 47–72.Google Scholar
Jhaveri, B. S. & Homsy, G. M. 1982 The onset of convection in fluid layers heated rapidly in a time-dependent manner. J. Fluid Mech. 114, 251–260.Google Scholar
Joseph, D. D. 1976 Stability of Fluid Motions. Springer.Google Scholar
Kaviany, M. 1984 Onset of thermal convection in a saturated porous medium: experiment and analysis. Int J. Heat Mass Transfer 27, 2101–2110.Google Scholar
Kim, M. C. & Choi, C. K. 2012 Linear stability analysis on the onset of buoyancy-driven convection in liquid-saturated porous medium. Phys. Fluids 24, 044102.Google Scholar
Kim, M. C. & Kim, S. 2005 Onset of convective instability in a fluid-saturated porous layer subject to time-depedent heating. Intl. Commun. Heat Mass Transfer 32, 416–424.Google Scholar
Lick, W. 1965 The instability of a fluid layer with time-dependent heating. J. Fluid Mech. 21, 565–576.Google Scholar
Malkus, W. V. R. & Veronis, G. 1958 Finite amplitude cellular convection. J. Fluid Mech. 4, 225–260.Google Scholar
Morton, B. R. 1957 On the equilibrium of a stratified layer of a fluid. J. Mech. Appl. Math. 10, 433–447.Google Scholar
Nayfeh, A. H. 1981 Introduction to Perturbation Techniques. John Wiley and Sons.Google Scholar
Orr, F. M. 2009 Onshore geologic storage of CO2. Science 325, 1656–1658.Google Scholar
Palm, E. 1960 On the tendency towards hexagonal cells in steady convection. J. Fluid Mech. 8, 183–192.Google Scholar
Pau, G. S. H., Bell, J. B., Pruess, K., Almgren, A. S., Lijewski, M. J. & Zhang, K. 2010 High-resolution simulation and characterization of density-driven flow in CO2 storage in saline aquifers. Adv. Water Resour. 33, 443–455.CrossRefGoogle Scholar
Peyret, R. 2002 Spectral Methods for Incompressible Viscous Flows. Springer-Verlag.Google Scholar
Pritchard, D. 2004 The instability of thermal and fluid fronts during radial injection in a porous medium. J. Fluid Mech. 508, 133–163.Google Scholar
Rapaka, S., Chen, S., Pawar, R. J., Stauffer, P. H. & Zhang, D. 2008 Non-modal growth of perturbations in density-driven convection in porous media. J. Fluid Mech. 609, 285–303.Google Scholar
Rees, D. A. S., Selim, A. & Ennis-King, J. P. 2008 The instability of unsteady boundary layers in porous media. In Emerging Topics in Heat and Mass Transfer in Porous Media (ed. Vadász, P.), pp. 85–110. Springer.Google Scholar
Riaz, A., Hesse, M., Tchelepi, A. & Orr, F. M. 2006 Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111.Google Scholar
Robinson, J. L. 1976 Theoretical analysis of convective instability of a growing horizontal thermal boundary layer. Phys. Fluids 19, 778–791.Google Scholar
Slim, A. C., Bandi, M. M., Miller, J. C. & Mahadevan, L. 2013 Dissolution-driven convection in a Hele-Shaw cell. Phys. Fluids 25, 024101.CrossRefGoogle Scholar
Slim, A. C. & Ramakrishnan, T. S. 2010 Onset and cessation of time-dependent, dissolution-driven convection in porous media. Phys. Fluids 22, 124103.Google Scholar
Spangenberg, W. G. & Rowland, W. R. 1961 Convective circulation in water induced by evaporation. Phys. Fluids 4, 743–750.Google Scholar
Sparrow, E. M., Beavers, G. S., Chen, T. S. & Lloyd, J. R. 1973 Breakdown of the laminar flow regime in permeable-walled ducts. J. Appl. Mech. 40, 337–342.Google Scholar
Tilton, N. & Cortelezzi, L. 2008 Linear stability analysis of pressure-driven flows in channels with porous walls. J. Fluid Mech. 604, 411–445.Google Scholar
Tilton, N., Daniel, D. & Riaz, A. 2013 The initial transient period of gravitationally unstable diffusive boundary layers developing in porous media. Phys. Fluids 25, 092107.Google Scholar
Whitaker, S. 1986 Flow in porous media I: a theoretical derivation of Darcy’s law. Trans. Porous Media 1, 3–25.Google Scholar
Whitaker, S. 1999 The Method of Volume Averaging. Klumer Academic Publishers.Google Scholar
Wooding, R. A., Tylers, S. W. & White, I. 1997 Convection in groundwater below an evaporating salt lake: 1. Onset of instability. Water Resour. Res. 33, 1199–1217.Google Scholar