Hostname: page-component-848d4c4894-cjp7w Total loading time: 0 Render date: 2024-06-23T23:27:36.489Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear ice sheet/liquid interaction in a channel with an obstruction

Published online by Cambridge University Press:  21 March 2024

B.-Y. Ni Open the ORCID record for B.-Y. Ni [Opens in a new window] ,
Y.A. Semenov Open the ORCID record for Y.A. Semenov [Opens in a new window] ,
T.I. Khabakhpasheva Open the ORCID record for T.I. Khabakhpasheva [Opens in a new window] ,
E.I. Părău Open the ORCID record for E.I. Părău [Opens in a new window]  and
A.A. Korobkin Open the ORCID record for A.A. Korobkin [Opens in a new window]
B.-Y. Ni
Affiliation:
College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, PR China
Y.A. Semenov*
Affiliation:
College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, PR China
T.I. Khabakhpasheva
Affiliation:
School of Mathematics, University of East Anglia, Norwich NR4 7TJ, UK
E.I. Părău
Affiliation:
School of Mathematics, University of East Anglia, Norwich NR4 7TJ, UK
A.A. Korobkin
Affiliation:
School of Mathematics, University of East Anglia, Norwich NR4 7TJ, UK
*
†Email address for correspondence: yuriy.a.semenov@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

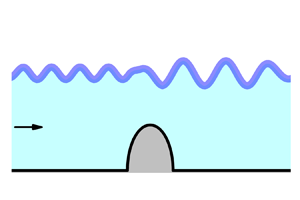
The interaction between the flow in a channel with an obstruction on the bottom and an elastic sheet representing the ice covering the liquid is considered for the case of steady flow. The mathematical model based on the velocity potential theory and the theory of thin elastic shells fully accounts for the nonlinear boundary conditions at the elastic sheet/liquid interface and on the bottom of the channel. The integral hodograph method is employed to derive the complex velocity potential of the flow, which contains the velocity magnitude at the interface in explicit form. This allows one to formulate the coupled ice/liquid interaction problem and reduce it to a system of nonlinear equations in the unknown magnitude of the velocity at the interface. Case studies are carried out for a semi-circular obstruction on the bottom of the channel. Three flow regimes are studied: a subcritical regime, for which the interface deflection decays upstream and downstream; an ice supercritical and channel subcritical regime, for which two waves of different lengths may exist; and a channel supercritical regime, for which the elastic wave is found to extend downstream to infinity. All these regimes are in full agreement with the dispersion equation. The obtained results demonstrate a strongly nonlinear interaction between the elastic and the gravity wave near the first critical Froude number where their lengths approach each other. The interface shape, the bending moment and the pressure along the interface are presented for wide ranges of the Froude number and the obstruction height.

JFM classification

Waves/Free-surface Flows: Elastic waves Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Wave-structure interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 983 , 25 March 2024 , A41
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Binder, B.J., Vanden-Broeck, J.-M. & Dias, F. 2009 On satisfying the radiation condition in free-surface flows. J. Fluid Mech. 624, 179–189.CrossRefGoogle Scholar
Blyth, M.G., Părău, E.I. & Vanden-Broeck, J.-M. 2011 Hydroelastic waves on fluid sheets. J. Fluid Mech. 689, 541–551.CrossRefGoogle Scholar
Bonnefoy, F., Meylan, M.H. & Ferrant, P. 2009 Nonlinear higher-order spectral solution for a two-dimensional moving load on ice. J. Fluid Mech. 621, 215–242.CrossRefGoogle Scholar
Brocklehurst, P., Korobkin, A. & Părău, E.I. 2011 Hydroelastic wave diffraction by a vertical cylinder. Phil. Trans. R. Soc. A 369, 2832–2851.CrossRefGoogle ScholarPubMed
Chaplygin, S.A. 1910 About Pressure of a Flat Flow on Obstacles. On the Airplane Theory. Moscow University.Google Scholar
Dias, F. & Vanden-Broeck, J.-M. 1989 Open channel flows with submerged obstructions. J. Fluid Mech. 206, 155–170.CrossRefGoogle Scholar
Dias, F. & Vanden-Broeck, J.-M. 2002 Generalised critical free-surface flows. J. Engng Maths 42, 291–301.CrossRefGoogle Scholar
Dias, F. & Vanden-Broeck, J.-M. 2004 Trapped waves between submerged obstacles. J. Fluid Mech. 509, 93–102.CrossRefGoogle Scholar
Forbes, L.K. & Schwartz, L.W. 1982 Free-surface flow over a semicircular obstruction. J. Fluid Mech. 114, 299–314.CrossRefGoogle Scholar
Gao, T., Wang, Z. & Milewski, P.A. 2019 Nonlinear hydroelastic waves on a linear shear current at finite depth. J. Fluid Mech. 876, 55–86.CrossRefGoogle Scholar
Greenhill, A.G. 1886 Wave motion in hydrodynamics. Am. J. Maths 9 (1), 62–96.CrossRefGoogle Scholar
Gurevich, M.I. 1965 Theory of Jets in Ideal Fluids. Academic Press.Google Scholar
Guyenne, P. & Părău, E.I. 2012 Computations of fully nonlinear hydroelastic solitary waves on deep water. J. Fluid Mech. 713, 307–329.CrossRefGoogle Scholar
Guyenne, P. & Părău, E.I. 2017 Numerical study of solitary wave attenuation in a fragmented ice sheet. Phys. Rev. Fluids 2, 034002.CrossRefGoogle Scholar
Joukowskii, N.E. 1890 Modification of Kirchhoff's method for determination of a fluid motion in two directions at a fixed velocity given on the unknown streamline. Math. Sbornik 15 (1), 121–278.Google Scholar
Karmakar, D., Bhattacharjee, J. & Sahoo, T. 2010 Oblique flexural gravity-wave scattering due to changes in bottom topography. J. Engng Maths 66, 325–341.CrossRefGoogle Scholar
Khabakhpasheva, T., Shishmarev, K. & Korobkin, A. 2019 Large-time response of ice cover to a load moving along a frozen channel. Appl. Ocean Res. 86, 154–165.CrossRefGoogle Scholar
Khabakhpasheva, T.I. & Korobkin, A.A. 2002 Hydroelastic behaviour of compound floating plate in waves. J. Engng Maths 44, 21–40.CrossRefGoogle Scholar
Kheisin, D.E. 1963 Moving load on an elastic plate which floats on the surface of an ideal fluid (in Russian). Izv. Akad. Nauk SSSR, Otd. Tekh. Nauk, Mekh. i Mashinostroenie 1, 178–180.Google Scholar
Kheisin, D.E. 1967 Dynamics of Floating Ice Cover, 215 p. (in Russian. Technical English Translation in: Tech. Rep. FSTC-HT-23-485-69, U.S. Army Foreign Science and Technology Center, 1969, Washington DC).Google Scholar
Kochin, N.E., Kibel, I.A. & Roze, N.V. 1964 Theoretical Hydromechanics. Wiley Interscience.Google Scholar
Korobkin, A., Părău, E.I. & Vanden-Broeck, J.-M. 2011 The mathematical challenges and modelling of hydroelasticity. Phil. Trans. R. Soc. Lond. A 369, 2803–2812.Google ScholarPubMed
Meylan, M.H., Bennetts, L.G., Mosig, J.E.M., Rogers, W.E., Doble, M. & Peter, M.A. 2018 Dispersion relations, power laws, and energy loss for waves in the marginal ice zone. J. Geophys. Res. Oceans 123, 3322–3335.CrossRefGoogle Scholar
Michell, J.H. 1890 On the theory of free streamlines. Phil. Trans. R. Soc. Lond. A 181, 389–431.Google Scholar
Milewski, P.A., Vanden-Broeck, J.M. & Wang, Z. 2011 Hydroelastic solitary waves in deep water. J. Fluid Mech. 679, 628–640.CrossRefGoogle Scholar
Ni, B.-Y., Han, D.-F., Di, S.-C. & Xue, Y.-Z. 2020 On the development of ice-water-structure interaction. J. Hydrodyn. 32 (4), 629–652.CrossRefGoogle Scholar
Ni, B.-Y., Khabakhpasheva, T.I. & Semenov, Y.A. 2023 Nonlinear gravity waves in the channel covered by broken ice. Phys. Fluids 35, 102118.CrossRefGoogle Scholar
Page, C. & Părău, E.I. 2014 Hydraulic falls under a floating ice plate due to submerged obstructions. J. Fluid Mech. 745, 208–222.CrossRefGoogle Scholar
Părău, E.I. & Dias, F. 2002 Nonlinear effects in the response of a floating ice plate to a moving load. J. Fluid Mech. 460, 281–305.CrossRefGoogle Scholar
Plotnikov, P.I. & Toland, J.F. 2011 Modelling nonlinear hydroelastic waves. Phil. Trans. R. Soc. A 369, 2942–2956.CrossRefGoogle ScholarPubMed
Pogorelova, A.V., Zemlyak, V.L. & Kozin, V.M. 2019 Moving of a submarine under an ice cover in fluid of finite depth. J. Hydrodyn. 31, 562–569.CrossRefGoogle Scholar
Porter, D. & Porter, R. 2004 Approximations to wave scattering by an ice sheet of variable thickness over undulating bed topography. J. Fluid Mech. 509, 145–179.CrossRefGoogle Scholar
Semenov, Y.A. 2021 Nonlinear flexural-gravity waves due to a body submerged in the uniform stream. Phys. Fluids 33 (5), 052115.CrossRefGoogle Scholar
Semenov, Y.A. & Cummings, L.J. 2007 Free boundary Darcy flows with surface tension: analytical and numerical study. Eur. J. Appl. Maths 17, 607–631.CrossRefGoogle Scholar
Semenov, Y.A. & Iafrati, A. 2006 On the nonlinear water entry problem of asymmetric wedges. J. Fluid Mech. 547, 231–256.CrossRefGoogle Scholar
Semenov, Y.A. & Yoon, B.-S. 2009 Onset of flow separation at oblique water impact of a wedge. Phys. Fluids 21, 112103–112111.CrossRefGoogle Scholar
Shishmarev, K., Khabakhpasheva, T. & Korobkin, A. 2016 The response of ice cover to a load moving along a frozen channel. Appl. Ocean Res. 59, 313–326.CrossRefGoogle Scholar
Shishmarev, K., Khabakhpasheva, T. & Oglezneva, K. 2023 Steady-state motion of a load on an ice cover with linearly variable thickness in a channel. J. Mar. Sci. Engng 11 (5), 1045.CrossRefGoogle Scholar
Shishmarev, K., Khabakhpasheva, T.I. & Korobkin, A.A. 2019 Ice response to an underwater body moving in a frozen channel. Appl. Ocean Res. 91, 101877.CrossRefGoogle Scholar
Squire, V.A. 2020 Ocean wave interactions with sea ice: a reappraisal. Annu. Rev. Fluid Mech. 52, 37–60.CrossRefGoogle Scholar
Squire, V.A., Dugan, J.P., Wadhams, P., Rottier, P.J. & Liu, A.K. 1995 Of ocean waves and sea ice. Annu. Rev. Fluid Mech. 27, 115–168.CrossRefGoogle Scholar
Squire, V.A., Hosking, R.J., Kerr, A.D. & Langhorne, P.J. 1996 Moving Loads on Ice Plates. Kluwer.CrossRefGoogle Scholar
Squire, V.A., Robinson, W.H., Langhorne, P.J. & Haskell, T.G. 1988 Vehicles and aircraft on floating ice. Nature 333, 159–161.CrossRefGoogle Scholar
Stepanyants, Y.A. & Sturova, I.V. 2021 Waves on a compressed floating ice plate caused by motion of a dipole in water. J. Fluid Mech. 907, A7.CrossRefGoogle Scholar
Sturova, I.V. 2009 Time-dependent response of a heterogeneous elastic plate floating on shallow water of variable depth. J. Fluid Mech. 637, 305–325.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 1987 Free-surface flow over an obstruction in a channel. Phys. Fluids 30, 2315–2317.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. & Părău, E.I. 2011 Two-dimensional generalized solitary waves and periodic waves under an ice sheet. Phil. Trans. R. Soc. A 369, 2957–2972.CrossRefGoogle ScholarPubMed
Xue, Y.Z., Zeng, L.D., Ni, B.Y., Korobkin, A.A. & Khabakhpasheva, T. 2021 Hydroelastic response of an ice sheet with a lead to a moving load. Phys. Fluids 33, 037109.CrossRefGoogle Scholar
Yuan, G.Y., Ni, B.Y., Wu, Q.G., Xue, Y.Z. & Han, D.F. 2022 Ice breaking by a high-speed water jet impact. J. Fluid Mech. 934, A1.CrossRefGoogle Scholar
Zhang, A.M., Li, S.M., Cui, P., Li, S. & Liu, Y.L. 2023 A unified theory for bubble dynamics. Phys. Fluids 35, 033323.CrossRefGoogle Scholar