Article contents
Nonlinear aspects of focusing internal waves
Published online by Cambridge University Press: 11 January 2019
Abstract
When a torus oscillates horizontally in a linearly stratified fluid, the wave rays form a double cone, one upward and one downward, with two focal points where the wave amplitude has a maximum due to wave focusing. Following a former study on linear aspects of wave focusing (Ermanyuk et al., J. Fluid Mech., vol. 813, 2017, pp. 695–715), we here consider experimental results on the nonlinear aspects that occur in the focal region below the torus for higher-amplitude forcing. A new non-dimensional number that is based on heuristic arguments for the wave amplitude in the focal area is presented. This focusing number is defined as 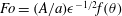 $Fo=(A/a)\unicode[STIX]{x1D716}^{-1/2}f(\unicode[STIX]{x1D703})$, with oscillation amplitude
$Fo=(A/a)\unicode[STIX]{x1D716}^{-1/2}f(\unicode[STIX]{x1D703})$, with oscillation amplitude 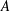 $A$,
$A$, 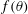 $f(\unicode[STIX]{x1D703})$ a function for the variation of the wave amplitude with wave angle
$f(\unicode[STIX]{x1D703})$ a function for the variation of the wave amplitude with wave angle 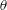 $\unicode[STIX]{x1D703}$, and
$\unicode[STIX]{x1D703}$, and 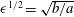 $\unicode[STIX]{x1D716}^{1/2}=\sqrt{b/a}$ the increase in amplitude due to the focusing, with
$\unicode[STIX]{x1D716}^{1/2}=\sqrt{b/a}$ the increase in amplitude due to the focusing, with  $a$ and
$a$ and 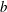 $b$, respectively, the minor and major radius of the torus. Nonlinear effects occur for
$b$, respectively, the minor and major radius of the torus. Nonlinear effects occur for 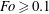 $Fo\geqslant 0.1$, with the shear stress giving rise to a mean flow which results in the focal region in a central upward motion partially surrounded by a downward motion. With increasing
$Fo\geqslant 0.1$, with the shear stress giving rise to a mean flow which results in the focal region in a central upward motion partially surrounded by a downward motion. With increasing 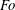 $Fo$, the Richardson number
$Fo$, the Richardson number 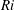 $Ri$ measured from the wave steepness monotonically decreases. Wave breaking occurs at
$Ri$ measured from the wave steepness monotonically decreases. Wave breaking occurs at 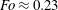 $Fo\approx 0.23$, corresponding to
$Fo\approx 0.23$, corresponding to 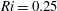 $Ri=0.25$. In this regime, the focal region is unstable due to triadic wave resonance. For the different tori sizes under consideration, the triadic resonant instability in these three-dimensional flows resembles closely the resonance observed by Bourget et al. (J. Fluid Mech., vol. 723, 2013, pp. 1–20) for a two-dimensional flow, with only minor differences. Application to internal tidal waves in the ocean are discussed.
$Ri=0.25$. In this regime, the focal region is unstable due to triadic wave resonance. For the different tori sizes under consideration, the triadic resonant instability in these three-dimensional flows resembles closely the resonance observed by Bourget et al. (J. Fluid Mech., vol. 723, 2013, pp. 1–20) for a two-dimensional flow, with only minor differences. Application to internal tidal waves in the ocean are discussed.
- Type
- JFM Rapids
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 8
- Cited by




