Article contents
Near-field mean flow dynamics of a cylindrical canopy patch suspended in deep water
Published online by Cambridge University Press: 08 November 2018
Abstract
The time-averaged flow dynamics of a suspended cylindrical canopy patch with a bulk diameter of 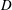 $D$ is investigated using large-eddy simulations (LES). The patch consists of
$D$ is investigated using large-eddy simulations (LES). The patch consists of  $N_{c}$ constituent solid circular cylinders of height
$N_{c}$ constituent solid circular cylinders of height 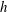 $h$ and diameter
$h$ and diameter 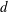 $d$, mimicking patchy vegetation suspended in deep water (
$d$, mimicking patchy vegetation suspended in deep water (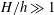 $H/h\gg 1$, where
$H/h\gg 1$, where 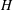 $H$ is the total flow depth). After validation against published data, LES of a uniform incident flow impinging on the canopy patch was conducted to study the effects of canopy density (
$H$ is the total flow depth). After validation against published data, LES of a uniform incident flow impinging on the canopy patch was conducted to study the effects of canopy density (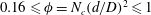 $0.16\leqslant \unicode[STIX]{x1D719}=N_{c}(d/D)^{2}\leqslant 1$, by varying
$0.16\leqslant \unicode[STIX]{x1D719}=N_{c}(d/D)^{2}\leqslant 1$, by varying 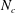 $N_{c}$) and bulk aspect ratio (
$N_{c}$) and bulk aspect ratio (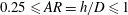 $0.25\leqslant AR=h/D\leqslant 1$, by varying
$0.25\leqslant AR=h/D\leqslant 1$, by varying 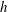 $h$) on the near-wake structure and adjustment of flow pathways. The relationships between patch geometry, local flow bleeding (three-dimensional redistribution of flow entering the patch) and global flow diversion (streamwise redistribution of upstream undisturbed flow) are identified. An increase in either
$h$) on the near-wake structure and adjustment of flow pathways. The relationships between patch geometry, local flow bleeding (three-dimensional redistribution of flow entering the patch) and global flow diversion (streamwise redistribution of upstream undisturbed flow) are identified. An increase in either 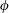 $\unicode[STIX]{x1D719}$ or
$\unicode[STIX]{x1D719}$ or 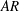 $AR$ decreases/increases/increases bleeding velocities through the patch surface area along the streamwise/lateral/vertical directions, respectively. However, a volumetric flux budget shows that a larger
$AR$ decreases/increases/increases bleeding velocities through the patch surface area along the streamwise/lateral/vertical directions, respectively. However, a volumetric flux budget shows that a larger 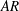 $AR$ causes a smaller proportion of the flow rate entering the patch to bleed out vertically. The global flow diversion is found to be determined by both the patch geometrical dimensions and the local bleeding which modifies the sizes of the patch-scale near wake. While loss of flow penetrating the patch increases monotonically with increasing
$AR$ causes a smaller proportion of the flow rate entering the patch to bleed out vertically. The global flow diversion is found to be determined by both the patch geometrical dimensions and the local bleeding which modifies the sizes of the patch-scale near wake. While loss of flow penetrating the patch increases monotonically with increasing 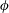 $\unicode[STIX]{x1D719}$, its partition into flow diversion around and beneath the patch shows a non-monotonic dependence. The spatial extents of the wake, the flow-diversion dynamics and the bulk drag coefficients of the patch jointly reveal the fundamental differences of flow responses between suspended porous patches and their solid counterparts.
$\unicode[STIX]{x1D719}$, its partition into flow diversion around and beneath the patch shows a non-monotonic dependence. The spatial extents of the wake, the flow-diversion dynamics and the bulk drag coefficients of the patch jointly reveal the fundamental differences of flow responses between suspended porous patches and their solid counterparts.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 19
- Cited by





