Article contents
Multi-point Monin–Obukhov similarity in the convective atmospheric surface layer using matched asymptotic expansions
Published online by Cambridge University Press: 11 February 2019
Abstract
The multi-point Monin–Obukhov similarity (MMO) was recently proposed (Tong & Nguyen, J. Atmos. Sci., vol. 72, 2015, pp. 4337–4348) to address the issue of incomplete similarity in the framework of the original Monin–Obukhov similarity theory (MOST). MMO hypothesizes the following: (1) The surface-layer turbulence, defined to consist of eddies that are entirely inside the surface layer, has complete similarity, which however can only be represented by multi-point statistics, requiring a horizontal characteristic length scale (absent in MOST). (2) The Obukhov length 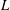 $L$ is also the characteristic horizontal length scale; therefore, all surface-layer multi-point statistics, non-dimensionalized using the surface-layer parameters, depend only on the height and separations between the points, non-dimensionalized using
$L$ is also the characteristic horizontal length scale; therefore, all surface-layer multi-point statistics, non-dimensionalized using the surface-layer parameters, depend only on the height and separations between the points, non-dimensionalized using 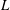 $L$. However, similar to MOST, MMO was also proposed as a hypothesis based on phenomenology. In this work we derive MMO analytically for the case of the horizontal Fourier transforms of the velocity and potential temperature fluctuations, which are equivalent to the two-point horizontal differences of these variables, using the spectral forms of the Navier–Stokes and the potential temperature equations. We show that, for the large-scale motions (wavenumber
$L$. However, similar to MOST, MMO was also proposed as a hypothesis based on phenomenology. In this work we derive MMO analytically for the case of the horizontal Fourier transforms of the velocity and potential temperature fluctuations, which are equivalent to the two-point horizontal differences of these variables, using the spectral forms of the Navier–Stokes and the potential temperature equations. We show that, for the large-scale motions (wavenumber 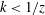 $k<1/z$) in a convective surface layer, the solution is uniformly valid with respect to
$k<1/z$) in a convective surface layer, the solution is uniformly valid with respect to  $z$ (i.e. as
$z$ (i.e. as  $z$ decreases from
$z$ decreases from 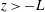 $z>-L$ to
$z>-L$ to 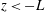 $z<-L$), where
$z<-L$), where  $z$ is the height from the surface. However, for
$z$ is the height from the surface. However, for 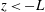 $z<-L$ the solution is not uniformly valid with respective to
$z<-L$ the solution is not uniformly valid with respective to 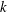 $k$ as it increases from
$k$ as it increases from 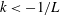 $k<-1/L$ to
$k<-1/L$ to 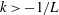 $k>-1/L$, resulting in a singular perturbation problem, which we analyse using the method of matched asymptotic expansions. We show that (1)
$k>-1/L$, resulting in a singular perturbation problem, which we analyse using the method of matched asymptotic expansions. We show that (1) 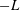 $-L$ is the characteristic horizontal length scale, and (2) the Fourier transforms satisfy MMO with the non-dimensional wavenumber
$-L$ is the characteristic horizontal length scale, and (2) the Fourier transforms satisfy MMO with the non-dimensional wavenumber 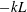 $-kL$ as the independent similarity variable. Two scaling ranges, the convective range and the dynamic range, discovered for
$-kL$ as the independent similarity variable. Two scaling ranges, the convective range and the dynamic range, discovered for 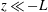 $z\ll -L$ in Tong & Nguyen (2015) are obtained. We derive the leading-order spectral scaling exponents for the two scaling ranges and the corrections to the scaling ranges for finite ratios of the length scales. The analysis also reveals the dominant dynamics in each scaling range. The analytical derivations of the characteristic horizontal length scale (
$z\ll -L$ in Tong & Nguyen (2015) are obtained. We derive the leading-order spectral scaling exponents for the two scaling ranges and the corrections to the scaling ranges for finite ratios of the length scales. The analysis also reveals the dominant dynamics in each scaling range. The analytical derivations of the characteristic horizontal length scale (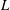 $L$) and the validity of MMO for the case of two-point horizontal separations provide strong support to MMO for general multi-point velocity and temperature differences.
$L$) and the validity of MMO for the case of two-point horizontal separations provide strong support to MMO for general multi-point velocity and temperature differences.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 7
- Cited by





