Article contents
The multi-mode stretched spiral vortex in homogeneous isotropic turbulence
Published online by Cambridge University Press: 08 January 2008
Abstract
The stretched spiral vortex is identified using direct numerical simulation (DNS) data for homogeneous isotropic turbulence and its properties are studied. Its genesis, growth and annihilation are elucidated, and its role in the generation of turbulence is shown. Aside from the two symmetric modes of configurations with regard to the vorticity alignment along two spiral sheets and the vortex tube in the core region studied in previous works, a third asymmetric mode is found. One of the two symmetric modes and the asymmetric mode are created not by a conventional rolling-up of a single vortex sheet but through the interaction among several sheets. The stagnation flow caused by the two sheets converges to form recirculating flow through its interaction with the vortex along the third sheet. This recirculating flow strains and stretches the sheets. The vortex tube is formed by axial straining, lowering of pressure and the intensification of the swirling motion in the recirculating region. As a result of the differential rotation induced by the tube and that self-induced by the sheet, the vortex sheets are entrained by the tube and form spiral turns. The transition between the three modes is examined. The initial configuration is in one of two symmetric modes, but it is transformed into another set of two modes due to the occurrence of reorientation in the vorticity direction along the stretched sheets. The symmetric mode tends to be more persistent than the asymmetric mode, among the two transformed modes. The tightening of the spiral turns of the spiral sheets produces a cascade of velocity fluctuations to smaller scales and generates a strongly intermittent dissipation field. To precisely capture the spiral turns, a grid resolution with at least 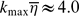 (kmax is the largest wavenumber,
(kmax is the largest wavenumber, 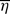 is the averaged Kolmogorov scale) is required. At a higher Reynolds number, self-similar spiral vortices are successively produced by the instability cascade along the stretched vortex sheets. A cluster consisting of spiral vortices with an extensive range of length scales is formed and this cluster induces an energy cascade.
is the averaged Kolmogorov scale) is required. At a higher Reynolds number, self-similar spiral vortices are successively produced by the instability cascade along the stretched vortex sheets. A cluster consisting of spiral vortices with an extensive range of length scales is formed and this cluster induces an energy cascade.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2008
References
REFERENCES
- 37
- Cited by




