Article contents
Motion and structure of atmospheric mesoscale baroclinic vortices: dry air and weak environmental shear
Published online by Cambridge University Press: 14 May 2012
Abstract
A strongly tilted, nearly axisymmetric vortex in dry air with asymmetric diabatic heating is analysed here by matched asymptotic expansions. The vortex is in gradient wind balance, with vortex Rossby numbers of order unity, and embedded in a quasi-geostrophic (QG) background wind with weak vertical shear. With wind speeds of 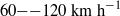 , such vortices correspond to tropical storms or nascent hurricanes according to the Saffir–Simpson scale. For asymmetric heating, nonlinear coupling of the evolution equations for the vortex tilt, its core structure, and its influence on the QG background is found. The theory compares well with the established linear theory of precessing quasi-modes of atmospheric vortices, and it corroborates the relationship between vortex tilt and asymmetric potential temperature and vertical velocity patterns as found by Jones (Q. J. R. Meteorol. Soc., vol. 121, 1995, pp. 821–851) and Frank & Ritchie (Mon. Weath. Rev., vol. 127, 1999, pp. 2044–2061) in simulations of adiabatic tropical cyclones. A relation between the present theory and the local induction approximation for three-dimensional slender vortex filaments is established.
, such vortices correspond to tropical storms or nascent hurricanes according to the Saffir–Simpson scale. For asymmetric heating, nonlinear coupling of the evolution equations for the vortex tilt, its core structure, and its influence on the QG background is found. The theory compares well with the established linear theory of precessing quasi-modes of atmospheric vortices, and it corroborates the relationship between vortex tilt and asymmetric potential temperature and vertical velocity patterns as found by Jones (Q. J. R. Meteorol. Soc., vol. 121, 1995, pp. 821–851) and Frank & Ritchie (Mon. Weath. Rev., vol. 127, 1999, pp. 2044–2061) in simulations of adiabatic tropical cyclones. A relation between the present theory and the local induction approximation for three-dimensional slender vortex filaments is established.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
Footnotes
Dr Owinoh passed away while this paper was under revision.
References
- 9
- Cited by




