Article contents
Model reduction and mechanism for the vortex-induced vibrations of bluff bodies
Published online by Cambridge University Press: 22 August 2017
Abstract
We present an effective reduced-order model (ROM) technique to couple an incompressible flow with a transversely vibrating bluff body in a state-space format. The ROM of the unsteady wake flow is based on the Navier–Stokes equations and is constructed by means of an eigensystem realization algorithm (ERA). We investigate the underlying mechanism of vortex-induced vibration (VIV) of a circular cylinder at low Reynolds number via linear stability analysis. To understand the frequency lock-in mechanism and self-sustained VIV phenomenon, a systematic analysis is performed by examining the eigenvalue trajectories of the ERA-based ROM for a range of reduced oscillation frequency 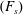 $(F_{s})$, while maintaining fixed values of the Reynolds number (
$(F_{s})$, while maintaining fixed values of the Reynolds number (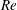 $Re$) and mass ratio (
$Re$) and mass ratio (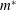 $m^{\ast }$). The effects of the Reynolds number
$m^{\ast }$). The effects of the Reynolds number 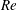 $Re$, the mass ratio
$Re$, the mass ratio 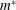 $m^{\ast }$ and the rounding of a square cylinder are examined to generalize the proposed ERA-based ROM for the VIV lock-in analysis. The considered cylinder configurations are a basic square with sharp corners, a circle and three intermediate rounded squares, which are created by varying a single rounding parameter. The results show that the two frequency lock-in regimes, the so-called resonance and flutter, only exist when certain conditions are satisfied, and the regimes have a strong dependence on the shape of the bluff body, the Reynolds number and the mass ratio. In addition, the frequency lock-in during VIV of a square cylinder is found to be dominated by the resonance regime, without any coupled-mode flutter at low Reynolds number. To further discern the influence of geometry on the VIV lock-in mechanism, we consider the smooth curve geometry of an ellipse and two sharp corner geometries of forward triangle and diamond-shaped bluff bodies. While the ellipse and diamond geometries exhibit the flutter and mixed resonance–flutter regimes, the forward triangle undergoes only the flutter-induced lock-in for
$m^{\ast }$ and the rounding of a square cylinder are examined to generalize the proposed ERA-based ROM for the VIV lock-in analysis. The considered cylinder configurations are a basic square with sharp corners, a circle and three intermediate rounded squares, which are created by varying a single rounding parameter. The results show that the two frequency lock-in regimes, the so-called resonance and flutter, only exist when certain conditions are satisfied, and the regimes have a strong dependence on the shape of the bluff body, the Reynolds number and the mass ratio. In addition, the frequency lock-in during VIV of a square cylinder is found to be dominated by the resonance regime, without any coupled-mode flutter at low Reynolds number. To further discern the influence of geometry on the VIV lock-in mechanism, we consider the smooth curve geometry of an ellipse and two sharp corner geometries of forward triangle and diamond-shaped bluff bodies. While the ellipse and diamond geometries exhibit the flutter and mixed resonance–flutter regimes, the forward triangle undergoes only the flutter-induced lock-in for 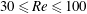 $30\leqslant Re\leqslant 100$ at
$30\leqslant Re\leqslant 100$ at  $m^{\ast }=10$. In the case of the forward triangle configuration, the ERA-based ROM accurately predicts the low-frequency galloping instability. We observe a kink in the amplitude response associated with 1:3 synchronization, whereby the forward triangular body oscillates at a single dominant frequency but the lift force has a frequency component at three times the body oscillation frequency. Finally, we present a stability phase diagram to summarize the VIV lock-in regimes of the five smooth-curve- and sharp-corner-based bluff bodies. These findings attempt to generalize our understanding of the VIV lock-in mechanism for bluff bodies at low Reynolds number. The proposed ERA-based ROM is found to be accurate, efficient and easy to use for the linear stability analysis of VIV, and it can have a profound impact on the development of control strategies for nonlinear vortex shedding and VIV.
$m^{\ast }=10$. In the case of the forward triangle configuration, the ERA-based ROM accurately predicts the low-frequency galloping instability. We observe a kink in the amplitude response associated with 1:3 synchronization, whereby the forward triangular body oscillates at a single dominant frequency but the lift force has a frequency component at three times the body oscillation frequency. Finally, we present a stability phase diagram to summarize the VIV lock-in regimes of the five smooth-curve- and sharp-corner-based bluff bodies. These findings attempt to generalize our understanding of the VIV lock-in mechanism for bluff bodies at low Reynolds number. The proposed ERA-based ROM is found to be accurate, efficient and easy to use for the linear stability analysis of VIV, and it can have a profound impact on the development of control strategies for nonlinear vortex shedding and VIV.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 52
- Cited by





