Article contents
Mathematical modelling of a viscida network
Published online by Cambridge University Press: 07 June 2019
Abstract
We develop a general model to describe a network of interconnected thin viscous sheets, or viscidas, which evolve under the action of surface tension. A junction between two viscidas is analysed by considering a single viscida containing a smoothed corner, where the centreline angle changes rapidly, and then considering the limit as the smoothing tends to zero. The analysis is generalized to derive a simple model for the behaviour at a junction between an arbitrary number of viscidas, which is then coupled to the governing equation for each viscida. We thus obtain a general theory, consisting of 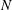 $N$ partial differential equations and
$N$ partial differential equations and 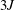 $3J$ algebraic conservation laws, for a system of
$3J$ algebraic conservation laws, for a system of 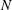 $N$ viscidas connected at
$N$ viscidas connected at 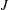 $J$ junctions. This approach provides a framework to understand the fabrication of microstructured optical fibres containing closely spaced holes separated by interconnected thin viscous struts. We show sample solutions for simple networks with
$J$ junctions. This approach provides a framework to understand the fabrication of microstructured optical fibres containing closely spaced holes separated by interconnected thin viscous struts. We show sample solutions for simple networks with 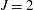 $J=2$ and
$J=2$ and 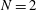 $N=2$ or 3. We also demonstrate that there is no uniquely defined junction model to describe interconnections between viscidas of different thicknesses.
$N=2$ or 3. We also demonstrate that there is no uniquely defined junction model to describe interconnections between viscidas of different thicknesses.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 1
- Cited by




