1 Introduction
Shock wave/turbulent boundary layer interactions (STBLIs) are typically unsteady across a broad range of frequencies. In addition to high-frequency unsteadiness, which is associated with turbulent fluctuations, STBLIs in the supersonic regime display a characteristic low-frequency unsteadiness (Dolling Reference Dolling2001; Smits & Dussauge Reference Smits and Dussauge2006; Clemens & Narayanaswamy Reference Clemens and Narayanaswamy2014). The low-frequency unsteadiness is present in separated STBLIs, i.e. when the shock is sufficiently strong to separate the boundary layer in the mean. In addition, evidence for low-frequency unsteadiness has also been observed when the probability of instantaneous flow separation is high but no mean flow separation is observed (Souverein et al. Reference Souverein, Dupont, Debiève, Dussauge, van Oudheusden and Scarano2010). The low-frequency unsteadiness, which is broadband, involves oscillations of the shock in the streamwise direction and corresponding variations in the size of the separated flow.
Dussauge, Dupont & Debiève (Reference Dussauge, Dupont and Debiève2006) surveyed STBLI experiments covering a range of Mach and Reynolds numbers and including different geometries for generating the shock, such as compression ramps, incident shocks and three-dimensional fins. They found that in the supersonic regime, the central frequency of the unsteadiness typically lies in the Strouhal number range
![]() $St=fL_{sep}/U_{\infty }=0.02-0.05$
, where
$St=fL_{sep}/U_{\infty }=0.02-0.05$
, where
![]() $L_{sep}$
is the length of the separated flow and
$L_{sep}$
is the length of the separated flow and
![]() $U_{\infty }$
is the free-stream velocity. These frequencies are significantly lower than the characteristic frequency of the turbulence in the incoming boundary layer, which is
$U_{\infty }$
is the free-stream velocity. These frequencies are significantly lower than the characteristic frequency of the turbulence in the incoming boundary layer, which is
![]() $f\unicode[STIX]{x1D6FF}/U_{\infty }=O(1)$
, where
$f\unicode[STIX]{x1D6FF}/U_{\infty }=O(1)$
, where
![]() $\unicode[STIX]{x1D6FF}$
is the boundary layer thickness.
$\unicode[STIX]{x1D6FF}$
is the boundary layer thickness.
In addition to being observed experimentally, the low-frequency unsteadiness is captured in a growing number of high-fidelity simulations. These include direct numerical simulations (DNS) and large eddy simulations (LES) of the compression-ramp configuration (Loginov, Adams & Zheltovodov Reference Loginov, Adams and Zheltovodov2006; Wu & Martín Reference Wu and Martín2007; Grilli et al. Reference Grilli, Schmid, Hickel and Adams2012; Priebe & Martín Reference Priebe and Martín2012; Grilli, Hickel & Adams Reference Grilli, Hickel and Adams2013) and of the reflected shock configuration (Pirozzoli & Grasso Reference Pirozzoli and Grasso2006; Priebe, Wu & Martín Reference Priebe, Wu and Martín2009; Touber & Sandham Reference Touber and Sandham2009; Hadjadj Reference Hadjadj2012; Aubard, Gloerfelt & Robinet Reference Aubard, Gloerfelt and Robinet2013; Morgan et al. Reference Morgan, Duraisamy, Nguyen, Kawai and Lele2013; Bermejo-Moreno et al. Reference Bermejo-Moreno, Campo, Larsson, Bodart, Helmer and Eaton2014).
The physics that is responsible for the low-frequency unsteadiness is not fully understood. Touber & Sandham (Reference Touber and Sandham2011) derived a model for the low-frequency unsteadiness by analysing the momentum integral equation in the context of reflected shock interactions. Their model, which is of the same form as that postulated by Plotkin (Reference Plotkin1975), shows that the shock/boundary layer interaction system behaves as a low-pass filter. External forcing is required to drive the model response. Physically, the required forcing could be provided by low-frequency content in either the incoming boundary layer or the separated flow downstream of the shock.
Several works in the literature have investigated the role of the incoming boundary layer in driving the low-frequency unsteadiness, see e.g. Beresh, Clemens & Dolling (Reference Beresh, Clemens and Dolling2002), Ganapathisubramani, Clemens & Dolling (Reference Ganapathisubramani, Clemens and Dolling2007, Reference Ganapathisubramani, Clemens and Dolling2009), and Humble, Scarano & van Oudheusden (Reference Humble, Scarano and van Oudheusden2009). Based on particle image velocimetry (PIV) measurements in a Mach 2 compression-ramp STBLI, Ganapathisubramani et al. (Reference Ganapathisubramani, Clemens and Dolling2007, Reference Ganapathisubramani, Clemens and Dolling2009) observed a correlation between the shock motion and streamwise-elongated regions of low and high momentum in the incoming boundary layer. They suggested that these large-scale boundary layer structures, which are also known as superstructures, play a role in driving the low-frequency unsteadiness.
In addition to the incoming boundary layer, much attention has also been focused on the role of the separated flow, downstream of the shock, as a possible source of low-frequency unsteadiness. The separated flow undergoes breathing motions, or pulsations, that correlate with the low-frequency excursions of the shock. The pulsations of the separated flow were initially observed from unsteady wall-pressure measurements, both in compression-ramp interactions (Erengil & Dolling Reference Erengil and Dolling1991; Thomas, Putnam & Chu Reference Thomas, Putnam and Chu1994) and in reflected shock interactions (Dupont, Haddad & Debiève Reference Dupont, Haddad and Debiève2006). The pulsations may also be seen in the velocity field, which can be obtained from PIV (e.g. Piponniau et al. Reference Piponniau, Dussauge, Debiève and Dupont2009) or from numerical simulation (e.g. Priebe & Martín Reference Priebe and Martín2012). It may be argued that the fact that the separated flow pulsates reveals little about the physical mechanism for the low-frequency unsteadiness, since such pulsations are not necessarily an indication of an inherent physical mechanism in the separated flow, but could be due to low-frequency disturbances in the incoming boundary layer convecting through the interaction.
Regarding possible physical mechanisms in the separated flow, several works in the literature have suggested that the shear layer, which is formed at the separation shock foot and evolves downstream, could play a role. The separated flow constitutes the low-speed side of the shear layer, and the free stream downstream of the shock constitutes the high-speed side. As shown by Dupont et al. (Reference Dupont, Haddad and Debiève2006), the shear layer shares many of the characteristics found in canonical plane mixing layers and incompressible shear layers. Due to the inflection point in the velocity profiles, the shear layer is unstable and large-scale vortical structures are formed, which have been observed in a number of STBLI studies (e.g. Dupont et al. Reference Dupont, Piponniau, Sidorenko and Debiève2008; Humble et al. Reference Humble, Scarano and van Oudheusden2009; Agostini et al. Reference Agostini, Larchevêque, Dupont, Debiève and Dussauge2012).
The characteristic frequency of the shear layer vortices in STBLIs is approximately
![]() $St\approx 0.5$
(Dupont et al.
Reference Dupont, Haddad and Debiève2006). Since this frequency is significantly higher than the frequencies of the shock unsteadiness, several mechanisms that would result in a low-frequency variation of the shear layer have been suggested, some of which are similar to physical scenarios proposed in the context of incompressible separated flows (Eaton & Johnston Reference Eaton, Johnston, Bradbury, Durst, Launder, Schmidt and Whitelaw1982; Kiya & Sasaki Reference Kiya and Sasaki1985; Lee & Sung Reference Lee and Sung2002).
$St\approx 0.5$
(Dupont et al.
Reference Dupont, Haddad and Debiève2006). Since this frequency is significantly higher than the frequencies of the shock unsteadiness, several mechanisms that would result in a low-frequency variation of the shear layer have been suggested, some of which are similar to physical scenarios proposed in the context of incompressible separated flows (Eaton & Johnston Reference Eaton, Johnston, Bradbury, Durst, Launder, Schmidt and Whitelaw1982; Kiya & Sasaki Reference Kiya and Sasaki1985; Lee & Sung Reference Lee and Sung2002).
Based on DNS results for a reflected STBLI, Pirozzoli & Grasso (Reference Pirozzoli and Grasso2006) found evidence for an acoustic feedback mechanism in the interaction. They suggested that downstream disturbances, which are generated, for example, by the interaction of the shear layer vortices with the incident shock, travel upstream through the low-speed region of the flow and affect the initial development of the shear layer near the separation shock foot, thus leading to a low-frequency feedback loop.
Piponniau et al. (Reference Piponniau, Dussauge, Debiève and Dupont2009) proposed a mechanism based on the entrainment of fluid by the shear layer. They determined the time scale required for the fluid in the separation bubble to be drained by shear layer entrainment. Since this time scale was found to agree favourably with the time scale of the shock unsteadiness, they suggested that the entrainment of fluid by the shear layer results in the low-frequency breathing of the separated flow. Based on DNS data of a Mach 2.9 compression-ramp STBLI, Priebe & Martín (Reference Priebe and Martín2012) found evidence for low-frequency variations of the turbulence intensity in the shear layer. The low-frequency dynamics of the flow could thus be driven by low-frequency variations of the shear layer, as had previously been proposed in the context of incompressible separated flows (Eaton & Johnston Reference Eaton, Johnston, Bradbury, Durst, Launder, Schmidt and Whitelaw1982; Kiya & Sasaki Reference Kiya and Sasaki1985; Lee & Sung Reference Lee and Sung2002).
The shear layer constitutes one source of instability in the flow. Linear stability analyses of incompressible laminar separated flows have shown that, in addition to the instability related to the shear layer, there is another instability related to the entire separated flow (e.g. Theofilis, Hein & Dallmann Reference Theofilis, Hein and Dallmann2000; Rodríguez & Theofilis Reference Rodríguez and Theofilis2010). A similar instability has also been found in the compressible regime by applying linear stability analysis to a laminar shock/boundary layer interaction (Robinet Reference Robinet2007).
The physical mechanism that is responsible for the linear instability of canonical laminar separated flows could also be present in turbulent shock/boundary layer interactions. Touber & Sandham (Reference Touber and Sandham2009) performed a global linear stability analysis of a Mach 2.3 reflected STBLI. The base flow for the stability analysis was the turbulent mean flow obtained from an LES, and the stability analysis showed an exponentially growing global mode in the interaction. This instability mode was also found by Pirozzoli et al. (Reference Pirozzoli, Larsson, Nichols, Bernardini, Morgan and Lele2010), who performed linear stability analysis of reflected STBLIs. In addition, Priebe & Martín (Reference Priebe and Martín2012) found evidence in their compression-ramp DNS of low-frequency structural changes occurring in the separated flow and shear layer. They noted that these structural changes are qualitatively similar to the linear instability modes reported in Touber & Sandham (Reference Touber and Sandham2009) and Pirozzoli et al. (Reference Pirozzoli, Larsson, Nichols, Bernardini, Morgan and Lele2010).
Another important aspect of STBLIs is the presence of large-scale streamwise vortices, which are usually attributed to a centrifugal mechanism that was first described in the context of laminar flows by Görtler (Reference Görtler1941). The streamwise vortices induce spanwise-alternating regions of low and high momentum (and temperature) and are visible in the skin friction (and surface heat transfer). In STBLI flows, these structures are most commonly observed using surface oil flow visualizations (e.g. Settles, Fitzpatrick & Bogdonoff Reference Settles, Fitzpatrick and Bogdonoff1979; Smits & Dussauge Reference Smits and Dussauge2006; Schülein & Trofimov Reference Schülein and Trofimov2011), and they have also been observed in the time-averaged flow obtained from LES (Loginov et al. Reference Loginov, Adams and Zheltovodov2006).
These previous works have focused on the time-averaged behaviour of the streamwise structures. As suggested by Loginov et al. (Reference Loginov, Adams and Zheltovodov2006) and Schülein & Trofimov (Reference Schülein and Trofimov2011), the structures are expected to display some degree of unsteadiness in a turbulent shock/boundary layer interaction, especially if steady disturbances in the upstream boundary layer, which tend to pin the structures to preferred spanwise locations, are absent or insignificant. In this paper, we present evidence for unsteady Görtler-type vortices in a Mach 3 compression-ramp STBLI. The unsteadiness is found to occur in the same range of low frequencies that is associated with the characteristic unsteadiness of the shock, which suggests that the shock unsteadiness and unsteady Görtler-type vortices are linked.
We investigate the low-frequency STBLI dynamics by applying dynamic mode decomposition (DMD) to a DNS that was previously reported in Priebe & Martín (Reference Priebe and Martín2012). Similar to the well-known proper orthogonal decomposition (POD), DMD is typically used to identify coherent structures in a flow field. However, unlike POD, DMD targets modes that are important to the dynamics of the flow evolution, rather than those that optimally reconstruct the flow. Each DMD mode has a corresponding DMD eigenvalue that captures its growth rate and frequency; as such DMD can be thought of as an extension of linear stability analysis to nonlinear dynamics (Schmid Reference Schmid2010). DMD can also be thought of as an approximation of Koopman spectral analysis (Rowley et al. Reference Rowley, Mezić, Bagheri, Schlatter and Henningson2009; Tu et al. Reference Tu, Rowley, Luchtenburg, Brunton and Kutz2014), providing further justification for its use in analysing nonlinear dynamics. In the context of STBLIs, the DMD method has previously been applied to LES data of a reflected shock interaction (Pirozzoli et al. Reference Pirozzoli, Larsson, Nichols, Bernardini, Morgan and Lele2010) and a compression-ramp interaction (Grilli et al. Reference Grilli, Schmid, Hickel and Adams2012). These previous works have shown the ability of DMD to capture the main features of the low-frequency STBLI dynamics, including the relevant frequencies and the pulsating nature of the separated flow dynamics.
The present analysis finds that the low-frequency dynamics observed in STBLIs is not associated with any single dominant DMD mode, but rather, it is the result of interactions between a number of low-frequency DMD modes. These modes each oscillate at different frequencies but all exhibit streamwise streaks in the downstream separation bubble. Together, they accurately reproduce the complex breathing behaviour characteristic of STBLIs.
The paper is organized as follows. Details of the numerical methods used in the DNS computations and the DMD analysis are given in § 2. The results of the DMD analysis are presented in § 3 and discussed in § 4, where a possible physical mechanism for the low-frequency unsteadiness is proposed. Conclusions are provided in § 5.
2 Numerical methods and computational set-up
2.1 Direct numerical simulation (DNS)
The DNS has previously been reported in Priebe & Martín (Reference Priebe and Martín2012). An overview of the simulation methodology and set-up is provided here; further details may be found in Priebe & Martín (Reference Priebe and Martín2012).
The DNS code implements a fourth-order weighted essentially non-oscillatory (WENO) scheme to discretize the convective fluxes, standard fourth-order central differences to discretize the viscous fluxes and a third-order low-storage Runge–Kutta scheme (Williamson Reference Williamson1980) to advance the solution in time. As described in Martín et al. (Reference Martín, Taylor, Wu and Weirs2006) and Taylor, Wu & Martín (Reference Taylor, Wu and Martín2007), the WENO scheme is optimized to reduce both the linear and nonlinear errors that are present in the original WENO formulation introduced by Jiang & Shu (Reference Jiang and Shu1996). Reducing these errors is necessary to accurately compute compressible flows involving both shock waves and turbulence.
Wu & Martín (Reference Wu and Martín2007) and Ringuette, Wu & Martín (Reference Ringuette, Wu and Martín2008) validated the DNS for a compression-ramp case against experiments at matching flow conditions (Bookey et al. Reference Bookey, Wyckham, Smits and Martín2005; Ringuette et al. Reference Ringuette, Bookey, Wyckham and Smits2009). The mean wall pressure, the separation length, several velocity profiles through the interaction and the fluctuating wall pressure were compared to experiments and good agreement was obtained.
The geometry under investigation in the present paper is a compression ramp with an angle of
![]() $24^{\circ }$
. The Mach number upstream of the interaction is
$24^{\circ }$
. The Mach number upstream of the interaction is
![]() $M_{\infty }=2.9$
, and the momentum-thickness Reynolds number is
$M_{\infty }=2.9$
, and the momentum-thickness Reynolds number is
![]() $Re_{\unicode[STIX]{x1D703}}=U_{\infty }\unicode[STIX]{x1D703}/\unicode[STIX]{x1D708}_{\infty }=2900$
, where
$Re_{\unicode[STIX]{x1D703}}=U_{\infty }\unicode[STIX]{x1D703}/\unicode[STIX]{x1D708}_{\infty }=2900$
, where
![]() $U_{\infty }$
is the free-stream velocity,
$U_{\infty }$
is the free-stream velocity,
![]() $\unicode[STIX]{x1D703}$
is the momentum thickness, and
$\unicode[STIX]{x1D703}$
is the momentum thickness, and
![]() $\unicode[STIX]{x1D708}_{\infty }$
is the kinematic viscosity in the free stream. The Reynolds number based on the ratio of the outer length scale to the inner, viscous length scale is
$\unicode[STIX]{x1D708}_{\infty }$
is the kinematic viscosity in the free stream. The Reynolds number based on the ratio of the outer length scale to the inner, viscous length scale is
![]() $\unicode[STIX]{x1D6FF}^{+}=\unicode[STIX]{x1D6FF}u_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D708}_{w}=340$
, where
$\unicode[STIX]{x1D6FF}^{+}=\unicode[STIX]{x1D6FF}u_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D708}_{w}=340$
, where
![]() $\unicode[STIX]{x1D6FF}$
is the boundary layer thickness,
$\unicode[STIX]{x1D6FF}$
is the boundary layer thickness,
![]() $u_{\unicode[STIX]{x1D70F}}$
is the friction velocity and
$u_{\unicode[STIX]{x1D70F}}$
is the friction velocity and
![]() $\unicode[STIX]{x1D708}_{w}$
is the kinematic viscosity at the wall.
$\unicode[STIX]{x1D708}_{w}$
is the kinematic viscosity at the wall.
The computational domain measures
![]() $L_{x}=14.3\unicode[STIX]{x1D6FF}$
in the streamwise direction and
$L_{x}=14.3\unicode[STIX]{x1D6FF}$
in the streamwise direction and
![]() $L_{y}=2.0\unicode[STIX]{x1D6FF}$
in the spanwise direction. The wall-normal extent of the domain
$L_{y}=2.0\unicode[STIX]{x1D6FF}$
in the spanwise direction. The wall-normal extent of the domain
![]() $L_{z}$
varies somewhat with the streamwise coordinate
$L_{z}$
varies somewhat with the streamwise coordinate
![]() $x$
; at the inlet of the computational domain,
$x$
; at the inlet of the computational domain,
![]() $L_{z}$
is
$L_{z}$
is
![]() $4.4\unicode[STIX]{x1D6FF}$
. Of the total streamwise domain length,
$4.4\unicode[STIX]{x1D6FF}$
. Of the total streamwise domain length,
![]() $7.9\unicode[STIX]{x1D6FF}$
are located upstream of the corner, while the remaining
$7.9\unicode[STIX]{x1D6FF}$
are located upstream of the corner, while the remaining
![]() $6.4\unicode[STIX]{x1D6FF}$
are located downstream of the corner (where this length is measured along the ramp surface). The domain is discretized using
$6.4\unicode[STIX]{x1D6FF}$
are located downstream of the corner (where this length is measured along the ramp surface). The domain is discretized using
![]() $N_{x}=1024$
grid points in the streamwise direction,
$N_{x}=1024$
grid points in the streamwise direction,
![]() $N_{y}=160$
grid points in the spanwise direction and
$N_{y}=160$
grid points in the spanwise direction and
![]() $N_{z}=128$
grid points in the wall-normal direction, resulting in a total grid size of
$N_{z}=128$
grid points in the wall-normal direction, resulting in a total grid size of
![]() $21$
million. Further details on the computational set-up, including grid resolutions, boundary conditions and initial conditions, may be found in Priebe & Martín (Reference Priebe and Martín2012).
$21$
million. Further details on the computational set-up, including grid resolutions, boundary conditions and initial conditions, may be found in Priebe & Martín (Reference Priebe and Martín2012).
The separation point signal for the DNS investigated in the present paper is shown in figure 1, which is adapted from Priebe & Martín (Reference Priebe and Martín2012). The signal extends over a time of approximately
![]() $200\unicode[STIX]{x1D6FF}/U_{\infty }$
, during which large-amplitude, low-frequency excursions of the separation point in the upstream and downstream direction are visible. As shown in Priebe & Martín (Reference Priebe and Martín2012), the DNS captures the low-frequency unsteadiness in agreement with previous STBLI experiments and simulations reported in the literature. To ensure adequate spatial and temporal resolution for the DMD analysis and to avoid aliasing, the three-dimensional DNS flow field is sampled at a relatively high frequency of approximately
$200\unicode[STIX]{x1D6FF}/U_{\infty }$
, during which large-amplitude, low-frequency excursions of the separation point in the upstream and downstream direction are visible. As shown in Priebe & Martín (Reference Priebe and Martín2012), the DNS captures the low-frequency unsteadiness in agreement with previous STBLI experiments and simulations reported in the literature. To ensure adequate spatial and temporal resolution for the DMD analysis and to avoid aliasing, the three-dimensional DNS flow field is sampled at a relatively high frequency of approximately
![]() $f_{s}\unicode[STIX]{x1D6FF}/U_{\infty }=10$
.
$f_{s}\unicode[STIX]{x1D6FF}/U_{\infty }=10$
.

Figure 1. Time evolution of the spanwise-averaged separation point illustrating the low-frequency unsteadiness in the DNS. Both the actual signal and the low-pass-filtered signal are shown. Adapted from figure 30 in Priebe & Martín (Reference Priebe and Martín2012).
2.2 Dynamic mode decomposition (DMD)
DMD is typically used to analyse fluid flows with complex temporal dynamics. It can be applied equally well to data from numerical simulations or experiments (Schmid Reference Schmid2010). The resulting DMD modes highlight dynamically important spatial structures, while the complex-valued DMD eigenvalues encode each mode’s associated growth rate and frequency. Like the more familiar POD, DMD is a purely data-based method and is suitable for the large datasets generated by high-fidelity simulations. However, while POD analysis is optimal for generating low-dimensional reconstructions of a dataset, DMD analysis targets dynamically relevant flow features. Formally, DMD can be thought of as an eigendecomposition of the best-fit linear approximation of the dynamics underlying a dataset (Tu et al. Reference Tu, Rowley, Luchtenburg, Brunton and Kutz2014). It can also be thought of as an approximation to Koopman spectral analysis (Rowley et al. Reference Rowley, Mezić, Bagheri, Schlatter and Henningson2009; Williams, Kevrekidis & Rowley Reference Williams, Kevrekidis and Rowley2015), making it applicable to nonlinear dynamics.
Of particular use, Koopman operator theory allows the decomposition of a nonlinearly evolving trajectory into a sum of oscillating modes, similar to the way the evolution of a linear system can be written as a sum of oscillating eigenvectors (Rowley et al.
Reference Rowley, Mezić, Bagheri, Schlatter and Henningson2009). For instance, consider a set of flow field measurements
![]() $\{q_{0},q_{1},\ldots ,q_{m}\}$
collected at a fixed sampling rate. We can express the evolution of this measurement in terms of Koopman modes
$\{q_{0},q_{1},\ldots ,q_{m}\}$
collected at a fixed sampling rate. We can express the evolution of this measurement in terms of Koopman modes
![]() $\unicode[STIX]{x1D703}_{j}$
, Koopman eigenvalues
$\unicode[STIX]{x1D703}_{j}$
, Koopman eigenvalues
![]() $\unicode[STIX]{x1D706}_{j}$
and scalar coefficients
$\unicode[STIX]{x1D706}_{j}$
and scalar coefficients
![]() $c_{j}$
as
$c_{j}$
as
Because DMD modes approximate Koopman modes, it is often instructive to consider a DMD reconstruction of the form
where
![]() $\unicode[STIX]{x1D719}_{j}$
is a DMD mode,
$\unicode[STIX]{x1D719}_{j}$
is a DMD mode,
![]() $d_{j}$
is a scalar coefficient and
$d_{j}$
is a scalar coefficient and
![]() $r$
is the number of modes used for the reconstruction. By isolating particular sets of mode indices
$r$
is the number of modes used for the reconstruction. By isolating particular sets of mode indices
![]() $j$
, we can characterize the contribution of particular DMD modes to the evolution of the flow field. For snapshots that are linearly consistent (Tu et al.
Reference Tu, Rowley, Luchtenburg, Brunton and Kutz2014), as is often the case with high-dimensional data, each DMD projection coefficient
$j$
, we can characterize the contribution of particular DMD modes to the evolution of the flow field. For snapshots that are linearly consistent (Tu et al.
Reference Tu, Rowley, Luchtenburg, Brunton and Kutz2014), as is often the case with high-dimensional data, each DMD projection coefficient
![]() $d_{j}$
in (2.2) necessarily encodes a (damped) oscillation, just as the scalar term
$d_{j}$
in (2.2) necessarily encodes a (damped) oscillation, just as the scalar term
![]() $c_{j}\unicode[STIX]{x1D706}_{j}^{k}$
does in (2.1). Rather than assume this form,
$c_{j}\unicode[STIX]{x1D706}_{j}^{k}$
does in (2.1). Rather than assume this form,
![]() $d_{j}$
can also be computed explicitly by using the adjoint DMD modes to perform a biorthogonal projection.
$d_{j}$
can also be computed explicitly by using the adjoint DMD modes to perform a biorthogonal projection.
We note that a similar decomposition could be obtained using Fourier analysis, for which the coefficients
![]() $d_{j}$
in (2.2) would be equally spaced along the unit circle. That is, each coefficient would have unit magnitude and the resulting frequencies would be uniformly distributed between zero and the Nyquist frequency. For the purpose of describing a dataset in terms of oscillating modes, Fourier analysis and DMD are both equally well suited. In this work we choose to use DMD due to its connections to Koopman operator theory and nonlinear dynamics.
$d_{j}$
in (2.2) would be equally spaced along the unit circle. That is, each coefficient would have unit magnitude and the resulting frequencies would be uniformly distributed between zero and the Nyquist frequency. For the purpose of describing a dataset in terms of oscillating modes, Fourier analysis and DMD are both equally well suited. In this work we choose to use DMD due to its connections to Koopman operator theory and nonlinear dynamics.
For our analysis, we collect 1700 samples (in time) of the flow field from the three-dimensional (3-D) DNS. We find the DMD results to be well-converged with respect to the sampling rate; the low-frequency DMD modes and eigenvalues do not vary much as we consider slower sampling rates of
![]() $f_{s,nom}/2$
,
$f_{s,nom}/2$
,
![]() $f_{s,nom}/5$
,
$f_{s,nom}/5$
,
![]() $f_{s,nom}/10$
and
$f_{s,nom}/10$
and
![]() $f_{s,nom}/20$
, where
$f_{s,nom}/20$
, where
![]() $f_{s,nom}$
is the nominal sampling frequency given in § 2.1, which produces 1700 samples. To lower computational costs, the 3-D flow fields are filtered and downsampled in the spanwise direction using the following equation:
$f_{s,nom}$
is the nominal sampling frequency given in § 2.1, which produces 1700 samples. To lower computational costs, the 3-D flow fields are filtered and downsampled in the spanwise direction using the following equation:
where
![]() $\bar{f}$
denotes filtered values,
$\bar{f}$
denotes filtered values,
![]() $f$
denotes unfiltered values and here we use
$f$
denotes unfiltered values and here we use
![]() $n=4$
. In addition to the 3-D flow fields, we also analyse spanwise-averaged (2-D) flow fields. The DMD modes and eigenvalues are computed in parallel using the modred library (Belson, Tu & Rowley Reference Belson, Tu and Rowley2014).
$n=4$
. In addition to the 3-D flow fields, we also analyse spanwise-averaged (2-D) flow fields. The DMD modes and eigenvalues are computed in parallel using the modred library (Belson, Tu & Rowley Reference Belson, Tu and Rowley2014).
For a compressible flow, it is natural to work with the conservative mass flux fields (
![]() $\unicode[STIX]{x1D70C}u$
,
$\unicode[STIX]{x1D70C}u$
,
![]() $\unicode[STIX]{x1D70C}v$
,
$\unicode[STIX]{x1D70C}v$
,
![]() $\unicode[STIX]{x1D70C}w$
), rather than the primitive velocity fields (
$\unicode[STIX]{x1D70C}w$
), rather than the primitive velocity fields (
![]() $u$
,
$u$
,
![]() $v$
,
$v$
,
![]() $w$
). Accordingly, we define the inner product between two flow fields
$w$
). Accordingly, we define the inner product between two flow fields
![]() $q_{1}$
and
$q_{1}$
and
![]() $q_{2}$
as
$q_{2}$
as
where
![]() $\mathscr{D}$
is the flow domain. We note that computationally, we work with the mass flux quantities
$\mathscr{D}$
is the flow domain. We note that computationally, we work with the mass flux quantities
![]() $\unicode[STIX]{x1D70C}u$
,
$\unicode[STIX]{x1D70C}u$
,
![]() $\unicode[STIX]{x1D70C}v$
and
$\unicode[STIX]{x1D70C}v$
and
![]() $\unicode[STIX]{x1D70C}w$
, rather than
$\unicode[STIX]{x1D70C}w$
, rather than
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $u$
,
$u$
,
![]() $v$
and
$v$
and
![]() $w$
individually. The choice of the inner product (2.4) is reasonable if we consider the norm it induces: two flow fields are considered to be ‘close together’ if their mass flux fields are everywhere close. In practice, we find that the DMD modes and eigenvalues do not vary much whether or not they are computed using a mass flux inner product or a velocity inner product. From a theoretical perspective, for a sequential time series like the one analysed here, DMD provides a decomposition of the form (2.1) that minimizes the residual in reconstructing the final snapshot of the dataset. The choice of inner product induces a norm that defines the magnitude of this residual. Since we are analysing a long dataset describing a stationary process, we expect this residual to be small, and thus the choice of inner product should have little effect.
$w$
individually. The choice of the inner product (2.4) is reasonable if we consider the norm it induces: two flow fields are considered to be ‘close together’ if their mass flux fields are everywhere close. In practice, we find that the DMD modes and eigenvalues do not vary much whether or not they are computed using a mass flux inner product or a velocity inner product. From a theoretical perspective, for a sequential time series like the one analysed here, DMD provides a decomposition of the form (2.1) that minimizes the residual in reconstructing the final snapshot of the dataset. The choice of inner product induces a norm that defines the magnitude of this residual. Since we are analysing a long dataset describing a stationary process, we expect this residual to be small, and thus the choice of inner product should have little effect.
For convenience, we can think of each snapshot of the mass flux field as a flattened 1-D vector. We can collect these snapshots/vectors into a matrix of mass flux fields. Then the DMD algorithm provides a linear transformation
![]() $T_{Q}$
that maps a matrix of mass flux snapshots
$T_{Q}$
that maps a matrix of mass flux snapshots
![]() $Q$
into a matrix of DMD modes
$Q$
into a matrix of DMD modes
![]() $\unicode[STIX]{x1D6F7}_{Q}$
:
$\unicode[STIX]{x1D6F7}_{Q}$
:
Since the columns of
![]() $Q$
are mass flux fields, so are the columns of
$Q$
are mass flux fields, so are the columns of
![]() $\unicode[STIX]{x1D6F7}_{Q}$
. The discretized mass flux field has the same dimension (number of elements) as the discretized velocity field, so we can apply the transformation
$\unicode[STIX]{x1D6F7}_{Q}$
. The discretized mass flux field has the same dimension (number of elements) as the discretized velocity field, so we can apply the transformation
![]() $T_{Q}$
to the matrix of velocity field snapshots
$T_{Q}$
to the matrix of velocity field snapshots
![]() $U$
. In § 3 we will do so in some cases as a convenient visualization strategy, as the velocity field tends to more clearly depict the behaviour of the modes in near-wall regions. We emphasize that the columns of
$U$
. In § 3 we will do so in some cases as a convenient visualization strategy, as the velocity field tends to more clearly depict the behaviour of the modes in near-wall regions. We emphasize that the columns of
![]() $UT_{Q}$
are not precisely equivalent to DMD modes computed using velocity field data, which would require a different, velocity-based inner product. However, in practice we find that visualizations of the columns of
$UT_{Q}$
are not precisely equivalent to DMD modes computed using velocity field data, which would require a different, velocity-based inner product. However, in practice we find that visualizations of the columns of
![]() $UT_{Q}$
are extremely similar to those of the velocity data DMD modes
$UT_{Q}$
are extremely similar to those of the velocity data DMD modes
![]() $\unicode[STIX]{x1D6F7}_{U}=UT_{U}$
.
$\unicode[STIX]{x1D6F7}_{U}=UT_{U}$
.
3 Results
3.1 DMD analysis of the three-dimensional flow field
To avoid overfitting the complex dynamics of the fully turbulent flow field, we first perform DMD analysis on a projection of the flow field, which we refer to as a ‘truncated DMD’. We choose a POD projection onto 43 modes (including the mean flow), as this retains 50 % of the perturbation energy. The resulting DMD spectrum is shown in figure 2. For each mode, we plot the magnitude of the mean projection coefficient over the time series (see (2.2)) against the mode frequency. In previous work (Priebe & Martín Reference Priebe and Martín2012), we have reported Fourier spectra of the wall pressure, the mass flux, and the separation and reattachment points for the present flow. The Fourier spectra show that most of the energy associated with the low-frequency motions is contained at Strouhal numbers below
![]() $0.1$
. As can be seen from the detailed view of the truncated DMD spectrum in figure 2(b), two energetic modes are present in the Strouhal number range of interest, at
$0.1$
. As can be seen from the detailed view of the truncated DMD spectrum in figure 2(b), two energetic modes are present in the Strouhal number range of interest, at
![]() $St=0.025$
and
$St=0.025$
and
![]() $St=0.049$
.
$St=0.049$
.

Figure 2. DMD spectrum for the (projected) 3-D flow field: the frequency range
![]() $St=0.0-1.25$
is shown in (a) and a detailed view of the low-frequency range up to a Strouhal number of
$St=0.0-1.25$
is shown in (a) and a detailed view of the low-frequency range up to a Strouhal number of
![]() $0.1$
is shown in (b).
$0.1$
is shown in (b).
Figure 3 shows the real parts of the low-frequency truncated DMD modes. The modes share a similar structure: significant perturbations are visible along the shock, in the separated flow, and in the downstream boundary layer on the ramp. Since the perturbations in the upstream boundary layer are weaker, they are not visible at the isocontour levels shown in figure 3. The perturbations along the shock have a high degree of two-dimensionality, at least in the free stream, away from the shock foot. In contrast, the perturbations in the separated flow and downstream boundary layer are three-dimensional and consist of two streamwise-elongated regions in which the perturbations of streamwise momentum
![]() $\unicode[STIX]{x1D70C}u$
are significant. The perturbations are of opposite sign in these two regions. Note that in figure 3, three regions of momentum perturbation, rather than two, are typically visible. However, two of these three regions are, in fact, connected and form a single, larger structure since the DNS is spanwise periodic. The perturbations along the shock are consistent with displacements of the shock sheet in the streamwise direction away from its average position. The structure of the 3-D DMD modes thus suggests that the low-frequency displacements of the shock are associated with streamwise-elongated regions of low and high momentum in the separated flow.
$\unicode[STIX]{x1D70C}u$
are significant. The perturbations are of opposite sign in these two regions. Note that in figure 3, three regions of momentum perturbation, rather than two, are typically visible. However, two of these three regions are, in fact, connected and form a single, larger structure since the DNS is spanwise periodic. The perturbations along the shock are consistent with displacements of the shock sheet in the streamwise direction away from its average position. The structure of the 3-D DMD modes thus suggests that the low-frequency displacements of the shock are associated with streamwise-elongated regions of low and high momentum in the separated flow.

Figure 3. Real part of the low-frequency (truncated) DMD modes. The mode structure is visualized by two isocontours of the streamwise mass flux:
![]() $\unicode[STIX]{x1D70C}u=-0.15$
is shown in blue and
$\unicode[STIX]{x1D70C}u=-0.15$
is shown in blue and
![]() $\unicode[STIX]{x1D70C}u=0.15$
in red. (a)
$\unicode[STIX]{x1D70C}u=0.15$
in red. (a)
![]() $St=0.025$
and (b)
$St=0.025$
and (b)
![]() $St=0.049$
.
$St=0.049$
.
The truncated DMD modes shown in figure 3 only capture the low-frequency dynamics present in a POD projection of the flow field that retains 50% of the perturbation energy. In order to more accurately reproduce the full low-frequency dynamics, specifically the time evolution of the low-pass-filtered separation point shown in figure 1, less aggressive truncation is required. We investigate projections with a perturbation energy content ranging from 25 % to 99 %, finding that increasing the dynamic content of the dataset results in additional DMD modes in the low-frequency range of interest. Interestingly, regardless of the truncation level, the same structure, consisting of streamwise-elongated regions of low and high momentum in the downstream flow, is present in all low-frequency DMD modes.
If we perform DMD analysis on the raw DNS data (i.e. without first performing a projection), we obtain the spectrum shown in figure 4(a), which shows a relatively continuous distribution of modes, with few distinct and isolated peaks. This is consistent with the fact that the flow dynamics under investigation is known to be broadband across a wide range of frequencies. Within the frequency range of interest, we see in figure 4(b) that there are five modes, compared to the two seen in figure 2(b). These low-frequency modes are listed in table 1. They are ordered according to their frequency: the lowest-frequency mode, which has a Strouhal number of
![]() $St=0.020$
, is designated as LF1, followed by LF2 at
$St=0.020$
, is designated as LF1, followed by LF2 at
![]() $St=0.040$
, LF3 at
$St=0.040$
, LF3 at
![]() $St=0.056$
, LF4 at
$St=0.056$
, LF4 at
![]() $St=0.075$
and LF5 at
$St=0.075$
and LF5 at
![]() $St=0.098$
; the prefix LF indicates a low-frequency mode. From figures 5 and 6, we observe that these modes all share the same structure, which also matches that of the truncated DMD modes shown in figure 3.
$St=0.098$
; the prefix LF indicates a low-frequency mode. From figures 5 and 6, we observe that these modes all share the same structure, which also matches that of the truncated DMD modes shown in figure 3.
For the remainder of the paper, we present the full (untruncated) DMD results. While we focus in part on modes LF1 and LF3, which are the two modes with the highest energy, we emphasize that all of the low-frequency modes shown in figure 4(b) and listed in table 1 are required to accurately reconstruct the low-frequency dynamics present in the DNS. In other words, when considering the full complexity of the flow field evolution, all of the low-frequency modes are dynamically relevant, which is consistent with the broadband nature of the unsteadiness. LF1 and LF3 are singled out only for illustrative purposes.

Figure 4. DMD spectrum for the 3-D flow field: the frequency range
![]() $St=0.0-5.0$
is shown in (a) and a detailed view of the low-frequency range up to a Strouhal number of approximately
$St=0.0-5.0$
is shown in (a) and a detailed view of the low-frequency range up to a Strouhal number of approximately
![]() $0.1$
is shown in (b). Rapidly decaying modes (
$0.1$
is shown in (b). Rapidly decaying modes (
![]() $|\unicode[STIX]{x1D706}|<0.995$
) are shown in light blue.
$|\unicode[STIX]{x1D706}|<0.995$
) are shown in light blue.
Table 1. Three-dimensional DMD modes at low frequencies.
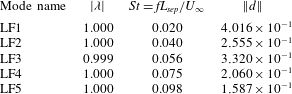

Figure 5. Real part of several low-frequency DMD modes visualized by two isocontours of the streamwise mass flux
![]() $\unicode[STIX]{x1D70C}u$
. (a) Mode LF1,
$\unicode[STIX]{x1D70C}u$
. (a) Mode LF1,
![]() $St=0.020$
, mass flux isocontour levels at
$St=0.020$
, mass flux isocontour levels at
![]() $\unicode[STIX]{x1D70C}u=-0.08$
in blue and
$\unicode[STIX]{x1D70C}u=-0.08$
in blue and
![]() $\unicode[STIX]{x1D70C}u=0.08$
in red; (b) mode LF2,
$\unicode[STIX]{x1D70C}u=0.08$
in red; (b) mode LF2,
![]() $St=0.040$
, mass flux isocontour levels at
$St=0.040$
, mass flux isocontour levels at
![]() $\unicode[STIX]{x1D70C}u=-0.14$
in blue and
$\unicode[STIX]{x1D70C}u=-0.14$
in blue and
![]() $\unicode[STIX]{x1D70C}u=0.14$
in red; and (c) mode LF3,
$\unicode[STIX]{x1D70C}u=0.14$
in red; and (c) mode LF3,
![]() $St=0.056$
, mass flux isocontour levels at
$St=0.056$
, mass flux isocontour levels at
![]() $\unicode[STIX]{x1D70C}u=-0.12$
in blue and
$\unicode[STIX]{x1D70C}u=-0.12$
in blue and
![]() $\unicode[STIX]{x1D70C}u=0.12$
in red.
$\unicode[STIX]{x1D70C}u=0.12$
in red.

Figure 6. Real part of several low-frequency DMD modes visualized by two isocontours of the streamwise mass flux
![]() $\unicode[STIX]{x1D70C}u$
. (a) Mode LF4,
$\unicode[STIX]{x1D70C}u$
. (a) Mode LF4,
![]() $St=0.075$
, mass flux isocontour levels at
$St=0.075$
, mass flux isocontour levels at
![]() $\unicode[STIX]{x1D70C}u=-0.12$
in blue and
$\unicode[STIX]{x1D70C}u=-0.12$
in blue and
![]() $\unicode[STIX]{x1D70C}u=0.12$
in red; and (b) mode LF5,
$\unicode[STIX]{x1D70C}u=0.12$
in red; and (b) mode LF5,
![]() $St=0.098$
, mass flux isocontour levels at
$St=0.098$
, mass flux isocontour levels at
![]() $\unicode[STIX]{x1D70C}u=-0.14$
in blue and
$\unicode[STIX]{x1D70C}u=-0.14$
in blue and
![]() $\unicode[STIX]{x1D70C}u=0.14$
in red.
$\unicode[STIX]{x1D70C}u=0.14$
in red.
Since each DMD mode is a complex-valued spatial field
![]() $\unicode[STIX]{x1D719}_{real}+i\unicode[STIX]{x1D719}_{imag}$
, we may calculate a corresponding phase angle
$\unicode[STIX]{x1D719}_{real}+i\unicode[STIX]{x1D719}_{imag}$
, we may calculate a corresponding phase angle
![]() $\unicode[STIX]{x1D6F9}=\tan ^{-1}(\unicode[STIX]{x1D719}_{imag}/\unicode[STIX]{x1D719}_{real})$
at each spatial location, with
$\unicode[STIX]{x1D6F9}=\tan ^{-1}(\unicode[STIX]{x1D719}_{imag}/\unicode[STIX]{x1D719}_{real})$
at each spatial location, with
![]() $\unicode[STIX]{x1D6F9}\in (-\unicode[STIX]{x03C0},\unicode[STIX]{x03C0}]$
. It is apparent from figure 7(a), which shows contours of the phase angle for mode LF1, that in the region of the flow occupied by the streamwise-elongated structures, the phase angle is approximately zero in the spanwise interval extending from
$\unicode[STIX]{x1D6F9}\in (-\unicode[STIX]{x03C0},\unicode[STIX]{x03C0}]$
. It is apparent from figure 7(a), which shows contours of the phase angle for mode LF1, that in the region of the flow occupied by the streamwise-elongated structures, the phase angle is approximately zero in the spanwise interval extending from
![]() $y/\unicode[STIX]{x1D6FF}\approx 1$
to
$y/\unicode[STIX]{x1D6FF}\approx 1$
to
![]() $y/\unicode[STIX]{x1D6FF}\approx 2$
, whereas it is approximately
$y/\unicode[STIX]{x1D6FF}\approx 2$
, whereas it is approximately
![]() $\pm \unicode[STIX]{x03C0}$
in the interval extending from
$\pm \unicode[STIX]{x03C0}$
in the interval extending from
![]() $y/\unicode[STIX]{x1D6FF}\approx 0$
to
$y/\unicode[STIX]{x1D6FF}\approx 0$
to
![]() $y/\unicode[STIX]{x1D6FF}\approx 1$
. This behaviour is highlighted in figure 7(b), which plots the phase angle against the spanwise coordinate at several streamwise and wall-normal locations in the downstream flow. The observed behaviour may be explained as follows: the perturbation amplitude is significantly higher in the real part of the mode (figure 8
a) as compared to the imaginary part (figure 8
b). As a result, the phase angle is either close to zero (large positive real part and small imaginary part) or close to
$y/\unicode[STIX]{x1D6FF}\approx 1$
. This behaviour is highlighted in figure 7(b), which plots the phase angle against the spanwise coordinate at several streamwise and wall-normal locations in the downstream flow. The observed behaviour may be explained as follows: the perturbation amplitude is significantly higher in the real part of the mode (figure 8
a) as compared to the imaginary part (figure 8
b). As a result, the phase angle is either close to zero (large positive real part and small imaginary part) or close to
![]() $\pm \unicode[STIX]{x03C0}$
(large negative real part and small imaginary part). Since the reconstruction of the time-dependent dynamics will consist of a rotation in the complex plane, from the real part of the mode to the imaginary part, the unsteadiness captured by mode LF1 involves significant variations of the strength of the streamwise-elongated structures, with both structures growing and fading in magnitude together.
$\pm \unicode[STIX]{x03C0}$
(large negative real part and small imaginary part). Since the reconstruction of the time-dependent dynamics will consist of a rotation in the complex plane, from the real part of the mode to the imaginary part, the unsteadiness captured by mode LF1 involves significant variations of the strength of the streamwise-elongated structures, with both structures growing and fading in magnitude together.
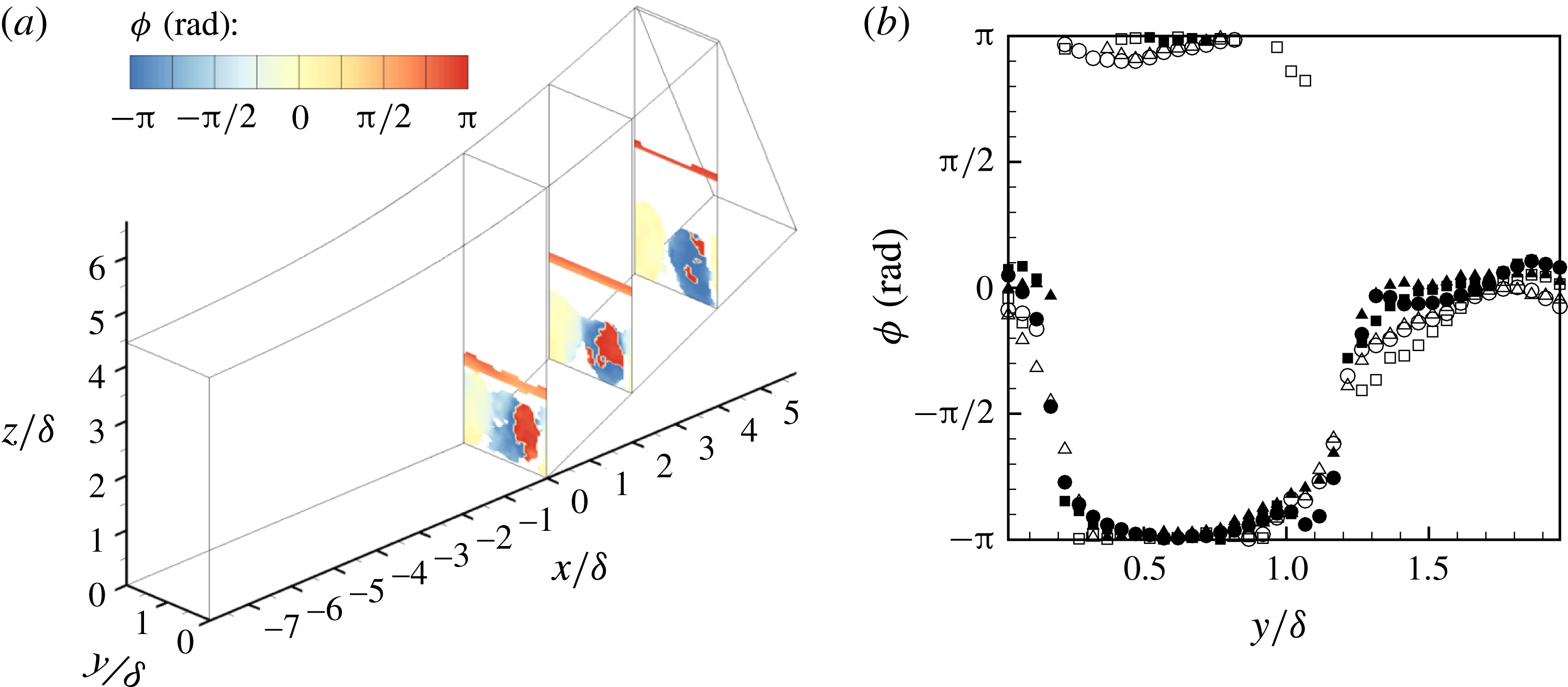
Figure 7. Phase angle plots for mode LF1. (a) Contours of the phase angle on three spanwise-wall-normal planes:
![]() $x/\unicode[STIX]{x1D6FF}=0.0$
,
$x/\unicode[STIX]{x1D6FF}=0.0$
,
![]() $x/\unicode[STIX]{x1D6FF}=2.0$
and
$x/\unicode[STIX]{x1D6FF}=2.0$
and
![]() $x/\unicode[STIX]{x1D6FF}=4.0$
. (b) Phase angle versus spanwise coordinate at two streamwise locations,
$x/\unicode[STIX]{x1D6FF}=4.0$
. (b) Phase angle versus spanwise coordinate at two streamwise locations,
![]() $x/\unicode[STIX]{x1D6FF}=2.0$
(open symbols) and
$x/\unicode[STIX]{x1D6FF}=2.0$
(open symbols) and
![]() $x/\unicode[STIX]{x1D6FF}=4.0$
(closed symbols) and at three wall-normal locations,
$x/\unicode[STIX]{x1D6FF}=4.0$
(closed symbols) and at three wall-normal locations,
![]() $(z-z_{w})/\unicode[STIX]{x1D6FF}=0.4$
(squares),
$(z-z_{w})/\unicode[STIX]{x1D6FF}=0.4$
(squares),
![]() $(z-z_{w})/\unicode[STIX]{x1D6FF}=0.6$
(circles) and
$(z-z_{w})/\unicode[STIX]{x1D6FF}=0.6$
(circles) and
![]() $(z-z_{w})/\unicode[STIX]{x1D6FF}=0.8$
(triangles), where
$(z-z_{w})/\unicode[STIX]{x1D6FF}=0.8$
(triangles), where
![]() $z_{w}$
is the coordinate of the wall. In both (a,b), the phase angle is only shown at points where the magnitude of the complex number representing the DMD mode is at least
$z_{w}$
is the coordinate of the wall. In both (a,b), the phase angle is only shown at points where the magnitude of the complex number representing the DMD mode is at least
![]() $10\,\%$
of the maximum magnitude encountered in the flow domain.
$10\,\%$
of the maximum magnitude encountered in the flow domain.

Figure 8. Low-frequency DMD mode LF1 visualized by contours of the streamwise mass flux
![]() $\unicode[STIX]{x1D70C}u$
. (a) Real part and (b) imaginary part.
$\unicode[STIX]{x1D70C}u$
. (a) Real part and (b) imaginary part.
As is apparent from figure 9, mode LF3 shows a different behaviour. In the region of the flow occupied by the streamwise-elongated structures, the phase angle tends to decrease as the spanwise coordinate
![]() $y$
is increased. The observed behaviour is consistent with a phase shift of approximately
$y$
is increased. The observed behaviour is consistent with a phase shift of approximately
![]() $\unicode[STIX]{x03C0}/2$
that exists in this region of the flow between the real and the imaginary part of the DMD mode. In other words, the streamwise-elongated structures present in the real part of the mode are shifted by a phase angle of approximately
$\unicode[STIX]{x03C0}/2$
that exists in this region of the flow between the real and the imaginary part of the DMD mode. In other words, the streamwise-elongated structures present in the real part of the mode are shifted by a phase angle of approximately
![]() $\unicode[STIX]{x03C0}/2$
, or equivalently by a spanwise distance of
$\unicode[STIX]{x03C0}/2$
, or equivalently by a spanwise distance of
![]() $\unicode[STIX]{x0394}y/\unicode[STIX]{x1D6FF}\approx 0.5$
, as compared to the imaginary part of the mode. The streamwise-elongated structures thus move in the spanwise direction from large to small
$\unicode[STIX]{x0394}y/\unicode[STIX]{x1D6FF}\approx 0.5$
, as compared to the imaginary part of the mode. The streamwise-elongated structures thus move in the spanwise direction from large to small
![]() $y$
(i.e. in the direction of increasing phase angle). Note that in the region of the flow occupied by the streamwise-elongated structures, mode LF3 also shows gradients of the phase angle in the wall-normal direction. At
$y$
(i.e. in the direction of increasing phase angle). Note that in the region of the flow occupied by the streamwise-elongated structures, mode LF3 also shows gradients of the phase angle in the wall-normal direction. At
![]() $x/\unicode[STIX]{x1D6FF}=4.0$
and between
$x/\unicode[STIX]{x1D6FF}=4.0$
and between
![]() $y/\unicode[STIX]{x1D6FF}\approx 1.5$
and
$y/\unicode[STIX]{x1D6FF}\approx 1.5$
and
![]() $y/\unicode[STIX]{x1D6FF}\approx 2$
, for example, the phase angle is higher near the wall than away from the wall (figure 9
a). This wall-normal gradient of the phase angle suggests that mode LF3 also involves wall-normal motions of the streamwise-elongated structures. Regarding the unsteady motion of the shock, we note that with increasing distance from the shock foot the phase angle increases along the shock, which implies that the low-frequency perturbations of the shock originate at the foot and travel outwards, away from the wall. This behaviour is seen both in mode LF1 (figure 7
a) and mode LF3 (figure 9
a).
$y/\unicode[STIX]{x1D6FF}\approx 2$
, for example, the phase angle is higher near the wall than away from the wall (figure 9
a). This wall-normal gradient of the phase angle suggests that mode LF3 also involves wall-normal motions of the streamwise-elongated structures. Regarding the unsteady motion of the shock, we note that with increasing distance from the shock foot the phase angle increases along the shock, which implies that the low-frequency perturbations of the shock originate at the foot and travel outwards, away from the wall. This behaviour is seen both in mode LF1 (figure 7
a) and mode LF3 (figure 9
a).

Figure 9. Phase angle plots for mode LF3. The phase angle is shown at the same spatial locations as in figure 7 and the same symbol key is used.
As is apparent from figure 10(a,b), mode LF2 has a similar phase angle behaviour as mode LF1. On the ramp, the phase angle is approximately zero between
![]() $y/\unicode[STIX]{x1D6FF}\approx 1.0$
and
$y/\unicode[STIX]{x1D6FF}\approx 1.0$
and
![]() $y/\unicode[STIX]{x1D6FF}\approx 1.6$
, and it is approximately
$y/\unicode[STIX]{x1D6FF}\approx 1.6$
, and it is approximately
![]() $\pm \unicode[STIX]{x03C0}$
between
$\pm \unicode[STIX]{x03C0}$
between
![]() $y/\unicode[STIX]{x1D6FF}\approx 0.0$
and
$y/\unicode[STIX]{x1D6FF}\approx 0.0$
and
![]() $y/\unicode[STIX]{x1D6FF}\approx 0.7$
. Between
$y/\unicode[STIX]{x1D6FF}\approx 0.7$
. Between
![]() $y/\unicode[STIX]{x1D6FF}\approx 0.7$
and
$y/\unicode[STIX]{x1D6FF}\approx 0.7$
and
![]() $y/\unicode[STIX]{x1D6FF}\approx 1.0$
, the amplitude of the real part of the mode is lower (see figure 5
b). In this region, spanwise gradients of the phase angle are visible, similar to the behaviour seen in mode LF3.
$y/\unicode[STIX]{x1D6FF}\approx 1.0$
, the amplitude of the real part of the mode is lower (see figure 5
b). In this region, spanwise gradients of the phase angle are visible, similar to the behaviour seen in mode LF3.
Mode LF4 (figure 10 c,d) has a similar phase angle behaviour as mode LF3. The spanwise gradient of the phase angle indicates that the streamwise-elongated regions move in the spanwise direction. Mode LF4 also shows wall-normal gradients of the phase angle indicating wall-normal motion.
The highest-frequency and lowest-energy mode considered here, mode LF5, shows a less well-defined phase angle behaviour, as is apparent from figure 10(e,f), although it appears that in the flow region occupied by the streamwise-elongated structures there is a general trend for increasing phase angle with increasing
![]() $y$
, which indicates a motion in the positive
$y$
, which indicates a motion in the positive
![]() $y$
direction.
$y$
direction.

Figure 10. Phase angle plots for modes: (a,b) LF2, (c,d) LF4 and (e,f) LF5. The phase angle is shown at the same spatial locations as in figure 7 and the same symbol key is used.

Figure 11. Pure oscillation based on mode LF3. One period of the dynamics is shown using eight uniformly spaced snapshots.
Based on the analysis of the phase angle, modes LF1 and LF2 demonstrate a first type of unsteadiness that the streamwise-elongated regions of low and high momentum can display: the strength of the positive and negative momentum perturbations can vary in time. A second and third type of unsteadiness are shown by modes LF3 and LF4 (and, to a lesser extent, by modes LF2 and LF5): the regions of low- and high-momentum perturbation can move in the spanwise direction, and they can move in the wall-normal direction.
To further describe the combination of spanwise and wall-normal motion captured by several of the modes, we have reconstructed the time-dependent dynamics based on mode LF3. Eight phase angles of the pure oscillation are shown in figure 11. The dynamics is of the form shown in (2.1), assuming a purely oscillatory eigenvalue and ignoring the scaling constant
![]() $c_{j}$
. As observed from the phase angle plots in figure 9, the perturbations associated with the shock originate at the shock foot and travel tangentially along the shock. This behaviour is visible, for example, in the sequence of figure 11(c–g), where a negative streamwise-momentum perturbation at the shock foot (visible in figure 11
c) travels along the shock, away from the wall and into the free stream (visible in the subsequent figure 11(d–g)). The pure oscillation in figure 11 also shows the low-frequency unsteadiness of the low- and high-momentum regions in the downstream flow. If one tracks the region of positive (or negative) momentum perturbation in time through the sequence of figure 11(a–h), it is apparent that both of these regions are unsteady. Consistent with the phase angle plots in figure 9, their motion can be described as a predominantly spanwise translation, at least based on the single mode LF3 considered here. At
$c_{j}$
. As observed from the phase angle plots in figure 9, the perturbations associated with the shock originate at the shock foot and travel tangentially along the shock. This behaviour is visible, for example, in the sequence of figure 11(c–g), where a negative streamwise-momentum perturbation at the shock foot (visible in figure 11
c) travels along the shock, away from the wall and into the free stream (visible in the subsequent figure 11(d–g)). The pure oscillation in figure 11 also shows the low-frequency unsteadiness of the low- and high-momentum regions in the downstream flow. If one tracks the region of positive (or negative) momentum perturbation in time through the sequence of figure 11(a–h), it is apparent that both of these regions are unsteady. Consistent with the phase angle plots in figure 9, their motion can be described as a predominantly spanwise translation, at least based on the single mode LF3 considered here. At
![]() $x/\unicode[STIX]{x1D6FF}=4.0$
, for example, the core of the positive momentum region is located at approximately
$x/\unicode[STIX]{x1D6FF}=4.0$
, for example, the core of the positive momentum region is located at approximately
![]() $y/\unicode[STIX]{x1D6FF}=1.0$
in figure 11(a), at approximately
$y/\unicode[STIX]{x1D6FF}=1.0$
in figure 11(a), at approximately
![]() $y/\unicode[STIX]{x1D6FF}=0.5$
in figure 11(c) and at approximately
$y/\unicode[STIX]{x1D6FF}=0.5$
in figure 11(c) and at approximately
![]() $y/\unicode[STIX]{x1D6FF}=0.0$
in figure 11(f). The negative momentum region also moves in the spanwise direction, but at a given instant its spanwise position is shifted by approximately
$y/\unicode[STIX]{x1D6FF}=0.0$
in figure 11(f). The negative momentum region also moves in the spanwise direction, but at a given instant its spanwise position is shifted by approximately
![]() $\unicode[STIX]{x0394}y/\unicode[STIX]{x1D6FF}=1$
with respect to the positive momentum region.
$\unicode[STIX]{x0394}y/\unicode[STIX]{x1D6FF}=1$
with respect to the positive momentum region.
In order to quantitatively describe the unsteadiness in the downstream separated flow, we detect the cores of the low- and high-momentum regions and track their positions in time. At fixed time
![]() $t$
and streamwise coordinate
$t$
and streamwise coordinate
![]() $x$
, the high-momentum core position vector
$x$
, the high-momentum core position vector
![]() $\overline{p_{h}}$
is calculated based on the following averaging procedure
$\overline{p_{h}}$
is calculated based on the following averaging procedure
 $$\begin{eqnarray}\overline{p_{h}}(x,t)=(\overline{y_{h}},\overline{z_{h}})(x,t)=\frac{\displaystyle \mathop{\sum }_{k=1}^{N}(\unicode[STIX]{x1D70C}u\unicode[STIX]{x0394}y\unicode[STIX]{x0394}z)_{h,k}p_{h,k}}{\displaystyle \mathop{\sum }_{k=1}^{N}(\unicode[STIX]{x1D70C}u\unicode[STIX]{x0394}y\unicode[STIX]{x0394}z)_{h,k}},\end{eqnarray}$$
$$\begin{eqnarray}\overline{p_{h}}(x,t)=(\overline{y_{h}},\overline{z_{h}})(x,t)=\frac{\displaystyle \mathop{\sum }_{k=1}^{N}(\unicode[STIX]{x1D70C}u\unicode[STIX]{x0394}y\unicode[STIX]{x0394}z)_{h,k}p_{h,k}}{\displaystyle \mathop{\sum }_{k=1}^{N}(\unicode[STIX]{x1D70C}u\unicode[STIX]{x0394}y\unicode[STIX]{x0394}z)_{h,k}},\end{eqnarray}$$
where
![]() $\{p_{h,k}\}_{k=1}^{N}$
is the set of
$\{p_{h,k}\}_{k=1}^{N}$
is the set of
![]() $N$
position vectors
$N$
position vectors
![]() $p_{h,k}=(y,z)_{h,k}$
, at which the largest values of the streamwise mass flux
$p_{h,k}=(y,z)_{h,k}$
, at which the largest values of the streamwise mass flux
![]() $\unicode[STIX]{x1D70C}u$
are encountered (at time
$\unicode[STIX]{x1D70C}u$
are encountered (at time
![]() $t$
and streamwise coordinate
$t$
and streamwise coordinate
![]() $x$
). The spanwise and wall-normal grid spacings are denoted by
$x$
). The spanwise and wall-normal grid spacings are denoted by
![]() $\unicode[STIX]{x0394}y$
and
$\unicode[STIX]{x0394}y$
and
![]() $\unicode[STIX]{x0394}z$
, respectively. The low-momentum core position vector
$\unicode[STIX]{x0394}z$
, respectively. The low-momentum core position vector
![]() $\overline{p_{l}}$
is calculated in a similar manner based on the set of position vectors
$\overline{p_{l}}$
is calculated in a similar manner based on the set of position vectors
![]() $\{p_{l,k}\}_{k=1}^{N}$
, at which the lowest values of the streamwise mass flux
$\{p_{l,k}\}_{k=1}^{N}$
, at which the lowest values of the streamwise mass flux
![]() $\unicode[STIX]{x1D70C}u$
are encountered.
$\unicode[STIX]{x1D70C}u$
are encountered.
We have repeated the analysis using several values of the averaging sample size ranging from
![]() $N=10$
to
$N=10$
to
![]() $N=250$
. Since the core trajectories are similar for all of the values of
$N=250$
. Since the core trajectories are similar for all of the values of
![]() $N$
investigated, the averaging procedure defined by equation (3.1) is relatively insensitive to the choice of the parameter
$N$
investigated, the averaging procedure defined by equation (3.1) is relatively insensitive to the choice of the parameter
![]() $N$
. Figure 12 shows the core trajectories at three streamwise stations along the ramp. Here, a sample size of
$N$
. Figure 12 shows the core trajectories at three streamwise stations along the ramp. Here, a sample size of
![]() $N=50$
is used.
$N=50$
is used.

Figure 12. Low- and high-momentum core positions for the pure oscillation based on mode LF3. Three different streamwise stations are shown:
![]() $x/\unicode[STIX]{x1D6FF}=0.0$
(squares),
$x/\unicode[STIX]{x1D6FF}=0.0$
(squares),
![]() $x/\unicode[STIX]{x1D6FF}=2.0$
(circles) and
$x/\unicode[STIX]{x1D6FF}=2.0$
(circles) and
![]() $x/\unicode[STIX]{x1D6FF}=4.0$
(triangles). Open symbols indicate the low-momentum core and closed symbols indicate the high-momentum core. A sample size
$x/\unicode[STIX]{x1D6FF}=4.0$
(triangles). Open symbols indicate the low-momentum core and closed symbols indicate the high-momentum core. A sample size
![]() $N=50$
is used for calculating the average core position. (a) Spanwise core position
$N=50$
is used for calculating the average core position. (a) Spanwise core position
![]() $y$
versus time, (b) wall-normal core position
$y$
versus time, (b) wall-normal core position
![]() $z$
versus time, (c) core trajectory in the spanwise-wall-normal plane and (d) magnitude of the average mass flux perturbation associated with the core versus time.
$z$
versus time, (c) core trajectory in the spanwise-wall-normal plane and (d) magnitude of the average mass flux perturbation associated with the core versus time.
It is apparent from figure 12 that the unsteady motion of the low- and high-momentum cores has components both in the spanwise direction and in the wall-normal direction. The low- and high-momentum cores translate monotonically in the spanwise direction as may be seen from figure 12(a). It is also apparent that the low- and high-momentum cores are shifted by a spanwise distance, which is on average approximately
![]() $\unicode[STIX]{x0394}y/\unicode[STIX]{x1D6FF}=1$
. A further observation that may be made from figure 12(a) is that the spanwise core position
$\unicode[STIX]{x0394}y/\unicode[STIX]{x1D6FF}=1$
. A further observation that may be made from figure 12(a) is that the spanwise core position
![]() $y$
depends on the streamwise location
$y$
depends on the streamwise location
![]() $x$
. For most of the times shown, as
$x$
. For most of the times shown, as
![]() $x$
is increased, the spanwise core position
$x$
is increased, the spanwise core position
![]() $y$
also increases, indicating that the loci of the low- and high-momentum core positions are not aligned perfectly with the streamwise direction but tend to be somewhat skewed away from the streamwise direction with a component in the spanwise direction.
$y$
also increases, indicating that the loci of the low- and high-momentum core positions are not aligned perfectly with the streamwise direction but tend to be somewhat skewed away from the streamwise direction with a component in the spanwise direction.
Figure 12(b) shows that, in addition to translating in the spanwise direction, the cores describe an unsteady motion in the wall-normal direction. The wall-normal motion of the positive core is essentially anti-correlated with that of the negative core, i.e. when the positive core is close to the wall, the negative core is farther away from the wall, and vice versa. The entire motion consisting of spanwise translation and up-and-down wall-normal motion is apparent from figure 12(c), which shows the core trajectories in the spanwise-wall-normal plane. A final observation that may be made about the unsteady motion of the low- and high-momentum regions is that the average perturbation strength associated with the cores is not constant but varies in time as shown in figure 12(d). Note that variations in the perturbation strength were also shown to be present in mode LF1 based on the behaviour of the phase angle (see figure 7).
In addition to computing a pure oscillation based on a single DMD mode, we have also reconstructed the dynamics based on combinations of several modes. The dynamics does not assume the form given by (2.1), but instead uses a truncated projection onto the DMD modes, i.e. a truncated form of (2.2) where the coefficients
![]() $d_{j}$
are computed using a biorthogonal projection. As more modes are added to the reconstruction, the low-frequency dynamics present in the DNS is approximated with increasing accuracy. As is apparent from figure 13, the reconstruction based on all of the low-frequency modes listed in table 1 (LF1 to LF5) accurately captures the low-frequency behaviour of the separation point: the correlation coefficient between the low-pass-filtered DNS signal and the reconstruction signal is
$d_{j}$
are computed using a biorthogonal projection. As more modes are added to the reconstruction, the low-frequency dynamics present in the DNS is approximated with increasing accuracy. As is apparent from figure 13, the reconstruction based on all of the low-frequency modes listed in table 1 (LF1 to LF5) accurately captures the low-frequency behaviour of the separation point: the correlation coefficient between the low-pass-filtered DNS signal and the reconstruction signal is
![]() $0.87$
. It should be noted that the DNS signal was low-pass filtered with a higher cutoff Strouhal number of
$0.87$
. It should be noted that the DNS signal was low-pass filtered with a higher cutoff Strouhal number of
![]() $0.22$
, so that additional, relatively low-energy DMD modes at Strouhal numbers between
$0.22$
, so that additional, relatively low-energy DMD modes at Strouhal numbers between
![]() $0.1$
and
$0.1$
and
![]() $0.22$
need to be added to the reconstruction to further improve the match between the actual and reconstructed separation point signals. The first 25% of the separation point signal from
$0.22$
need to be added to the reconstruction to further improve the match between the actual and reconstructed separation point signals. The first 25% of the separation point signal from
![]() $tU_{\infty }/L_{sep}=112.8$
to
$tU_{\infty }/L_{sep}=112.8$
to
![]() $tU_{\infty }/L_{sep}=127.5$
, in particular, appear to show some higher-frequency contributions. If this part of the signal is excluded, the correlation coefficient between the low-pass-filtered DNS signal and the reconstruction signal is
$tU_{\infty }/L_{sep}=127.5$
, in particular, appear to show some higher-frequency contributions. If this part of the signal is excluded, the correlation coefficient between the low-pass-filtered DNS signal and the reconstruction signal is
![]() $0.96$
.
$0.96$
.

Figure 13. Comparison between the original DNS data and the reconstruction based on all of the relevant low-frequency DMD modes. The comparison is shown in terms of the separation point
![]() $x_{s}$
. The DNS is shown in black, and the reconstruction based on modes LF1, LF2, LF3, LF4 and LF5 in red. Note that this figure is identical to figure 1, except that the DMD reconstruction has been added.
$x_{s}$
. The DNS is shown in black, and the reconstruction based on modes LF1, LF2, LF3, LF4 and LF5 in red. Note that this figure is identical to figure 1, except that the DMD reconstruction has been added.
A movie of the low-frequency dynamics reconstructed based on modes LF1 to LF5 is available with the online version of this paper at http://dx.doi.org/
10.1017/jfm.2016.557. Four uncorrelated snapshots of the reconstruction are shown in figure 14, and the core-tracking results for the reconstruction are shown in figure 15. As is apparent from figures 14 and 15, the many-mode reconstruction shows similar dynamics as the dynamics observed in the pure oscillation. Regarding the streamwise motions of the shock, figure 14(a) shows a snapshot in which the shock is located upstream of its average position (positive
![]() $\unicode[STIX]{x1D70C}u$
perturbation along the shock), whereas figure 14(c) shows a snapshot in which the shock is located downstream (negative
$\unicode[STIX]{x1D70C}u$
perturbation along the shock), whereas figure 14(c) shows a snapshot in which the shock is located downstream (negative
![]() $\unicode[STIX]{x1D70C}u$
perturbation). In figures 14(b) and 14(d), the shock is located closer to its average position (near-zero perturbation along the shock). The streamwise-elongated structures and their unsteady motion are also visible. The perturbation strength associated with the structures varies and is stronger in figure 14(a,b,d) than in figure 14(c). In addition, the structures are unsteady in the spanwise and wall-normal directions. The spanwise motion, for example, is apparent by comparing figures 14(b) and 14(d); the spanwise location of the low- and high-momentum regions is approximately interchanged between these two snapshots. The three types of unsteadiness associated with the streamwise-elongated structures are shown quantitatively in figure 15: the structures move along the span (figure 15
a), they move in the wall-normal direction (figure 15
b) and their intensity varies (figure 15
c). While there are strong similarities between the many-mode dynamics shown here and the pure oscillation shown in figures 11 and 12, there is also a key difference: while the spanwise motion in the pure oscillation is monotonic, the inclusion of many modes leads to a more complex, non-monotonic spanwise motion (see figure 15
a).
$\unicode[STIX]{x1D70C}u$
perturbation). In figures 14(b) and 14(d), the shock is located closer to its average position (near-zero perturbation along the shock). The streamwise-elongated structures and their unsteady motion are also visible. The perturbation strength associated with the structures varies and is stronger in figure 14(a,b,d) than in figure 14(c). In addition, the structures are unsteady in the spanwise and wall-normal directions. The spanwise motion, for example, is apparent by comparing figures 14(b) and 14(d); the spanwise location of the low- and high-momentum regions is approximately interchanged between these two snapshots. The three types of unsteadiness associated with the streamwise-elongated structures are shown quantitatively in figure 15: the structures move along the span (figure 15
a), they move in the wall-normal direction (figure 15
b) and their intensity varies (figure 15
c). While there are strong similarities between the many-mode dynamics shown here and the pure oscillation shown in figures 11 and 12, there is also a key difference: while the spanwise motion in the pure oscillation is monotonic, the inclusion of many modes leads to a more complex, non-monotonic spanwise motion (see figure 15
a).

Figure 14. Reconstruction of the low-frequency dynamics based on modes LF1, LF2, LF3, LF4 and LF5. Four uncorrelated snapshots are shown. In addition, a movie of the reconstruction is available with the online version of this paper.

Figure 15. Low- and high-momentum core positions for the reconstruction of the dynamics based on modes LF1, LF2, LF3, LF4 and LF5. (a) Spanwise core position
![]() $y$
versus time at
$y$
versus time at
![]() $x/\unicode[STIX]{x1D6FF}=4.0$
; (b) wall-normal core position
$x/\unicode[STIX]{x1D6FF}=4.0$
; (b) wall-normal core position
![]() $z$
versus time at three different streamwise stations:
$z$
versus time at three different streamwise stations:
![]() $x/\unicode[STIX]{x1D6FF}=0.0$
(squares),
$x/\unicode[STIX]{x1D6FF}=0.0$
(squares),
![]() $x/\unicode[STIX]{x1D6FF}=2.0$
(circles) and
$x/\unicode[STIX]{x1D6FF}=2.0$
(circles) and
![]() $x/\unicode[STIX]{x1D6FF}=4.0$
(triangles); and (c) magnitude of the average mass flux perturbation associated with the core versus time at
$x/\unicode[STIX]{x1D6FF}=4.0$
(triangles); and (c) magnitude of the average mass flux perturbation associated with the core versus time at
![]() $x/\unicode[STIX]{x1D6FF}=4.0$
. Open symbols indicate the low-momentum core and closed symbols indicate the high-momentum core. A sample size
$x/\unicode[STIX]{x1D6FF}=4.0$
. Open symbols indicate the low-momentum core and closed symbols indicate the high-momentum core. A sample size
![]() $N=50$
is used for calculating the average core position.
$N=50$
is used for calculating the average core position.
3.2 Two-dimensional DMD modes
While the perturbations in the downstream separated flow are spanwise dependent, the perturbations associated with the shock display a high degree of uniformity across the span of the computational domain, at least in the free stream, away from the foot of the shock which tends to display some variation in the spanwise direction. The two-dimensionality of the shock is apparent from figures 3, 7–11 and 14. As discussed in Wu & Martín (Reference Wu and Martín2008) and Priebe & Martín (Reference Priebe and Martín2012), a significantly wider computational domain would be required to capture any possible 3-D effects associated with the low-frequency shock motion.
The two-dimensionality of the low-frequency shock motion was also shown in Priebe & Martín (Reference Priebe and Martín2012), where a coherence analysis of pressure signals across the span of the computational domain was performed. The analysis showed that pressure signals obtained in the region of shock motion at different spanwise locations have a coherence of almost one at the low frequencies of interest. This indicates that the signals are related almost linearly across the span of the domain. Since the signals were also shown to be in phase, it was concluded that the low-frequency shock motion is essentially two-dimensional across the spanwise width of the present computational domain.
The two-dimensionality of the shock provides the justification for analysing the low-frequency dynamics from spanwise-averaged fields in addition to the full 3-D fields. The spanwise-averaged fields and modes show the net 2-D effect of the inherently 3-D separated flow dynamics that drives the shock. Two different approaches are used here: the 2-D dynamics is first investigated by spanwise averaging the 3-D DMD modes. Second, we apply the DMD method directly to the spanwise-averaged DNS flow field. This second approach is of interest, since it is computationally cheaper than applying the DMD analysis to the 3-D flow field.
3.2.1 Spanwise average of the 3-D DMD modes
We have spanwise averaged the reconstruction of the dynamics based on the 3-D DMD modes LF1–LF5. The resulting 2-D and time-dependent flow field reveals structural changes that occur in the separation bubble during the low-frequency shock motions. Two particularly clear examples of these structural changes are shown in figures 16(a,b) and 16(c,d). In both cases, a similar change is shown, from figures 16(a) to 16(b), and similarly from figures 16(c) to 16(d). In all of the snapshots, significant streamwise velocity perturbations are present in the following regions of the flow: along the shock, in the separation bubble and in the separated shear layer, as well as in the out-of-equilibrium boundary layer downstream of reattachment. Compared with the strong perturbations in the flow downstream of the shock, the perturbations in the incoming boundary layer upstream of the shock are relatively weak.

Figure 16. Two-dimensional field of
![]() $u$
perturbation obtained by spanwise averaging the reconstruction of the dynamics based on the 3-D DMD modes LF1–LF5. Snapshot (b) occurs
$u$
perturbation obtained by spanwise averaging the reconstruction of the dynamics based on the 3-D DMD modes LF1–LF5. Snapshot (b) occurs
![]() $\unicode[STIX]{x0394}tU_{\infty }/L_{sep}=5.6$
after snapshot (a) and snapshot (d) occurs
$\unicode[STIX]{x0394}tU_{\infty }/L_{sep}=5.6$
after snapshot (a) and snapshot (d) occurs
![]() $\unicode[STIX]{x0394}tU_{\infty }/L_{sep}=3.2$
after snapshot (c). The first pair of snapshots (a,b) is uncorrelated with the second pair (c,d).
$\unicode[STIX]{x0394}tU_{\infty }/L_{sep}=3.2$
after snapshot (c). The first pair of snapshots (a,b) is uncorrelated with the second pair (c,d).
If we focus on the structure of the flow up to reattachment, five distinct regions of significant, positive or negative, perturbation may be identified from figure 16(a) (or similarly figure 16
c). To aid in the description, these regions are encircled and labelled in the figure. The region of negative perturbation labelled A1 coincides with the shock, extending from the shock foot in the boundary layer to the free stream. Since the streamwise velocity
![]() $u$
decreases as the shock is traversed in the direction of increasing streamwise coordinate
$u$
decreases as the shock is traversed in the direction of increasing streamwise coordinate
![]() $x$
, a negative perturbation in this region implies that the shock is located upstream of its time-averaged position. Region A2, a streamwise-elongated region of negative perturbation, coincides with the shear layer and the reattaching boundary layer. Since the sign of the perturbation in region A2 is the same as along the shock in region A1, the upstream displacement of the shock is linked with a negative velocity perturbation in region A2, which is consistent with a larger separation bubble and a shear layer that is farther away from the wall.
$x$
, a negative perturbation in this region implies that the shock is located upstream of its time-averaged position. Region A2, a streamwise-elongated region of negative perturbation, coincides with the shear layer and the reattaching boundary layer. Since the sign of the perturbation in region A2 is the same as along the shock in region A1, the upstream displacement of the shock is linked with a negative velocity perturbation in region A2, which is consistent with a larger separation bubble and a shear layer that is farther away from the wall.
In addition to region A2, three other regions of significant perturbation, which are labelled as regions A3, A4 and A5 in figure 16(a,c), are visible in the flow downstream of separation. These regions occupy near-wall patches of the flow domain: region A3 is located a short distance downstream of separation, region A5 is located around the corner and region A4 is located near reattachment. Crucially, the perturbation in two of these regions (A3 and A4) is of opposite sign as compared to regions A1 or A2. This implies that when the shock is located in an upstream position (negative perturbation in region A1), the outer part of the shear layer and the separation bubble are characterized by a negative velocity perturbation (region A2), whereas in two near-wall regions, one near separation (region A3) and the other closer to reattachment (region A4), the velocity perturbation carries the opposite sign and is positive. In other words, the velocity perturbation is not negative everywhere in the shear layer and in the separation bubble when the shock is located upstream. Instead, the perturbation is positive and the reversed flow is weakened in regions A3 and A4, implying that the flow is locally reattaching and the bubble is collapsing in these two regions. We note that regions A3 and A4 may also be regarded as a single, connected region of positive perturbation that arches over the corner.
As discussed, the snapshots in figure 16(a,c) show significant negative perturbations along the shock, implying that the shock is displaced upstream. In contrast, the snapshots in figure 16(b,d) show only weak perturbations along the lower part of the shock, which implies that this part of the shock is located near its average position. The shock has thus moved downstream between snapshots (a,c) and (b,d), and snapshots (b,d) correspond to the instants when the shock foot passes through its time-averaged position while translating downstream.
It is apparent that snapshots (b) and (d) have a simpler perturbation structure in the separation bubble and in the separated shear layer than snapshots (a) and (c). The perturbation is positive in most of the separation bubble and shear layer (region B1), which is consistent with a weaker-than-average reversed flow and, consequently, a smaller separation bubble and a shear layer that is located closer to the wall. A further point to note from figure 16(b,d) is that an additional region of significant perturbation is visible in the reattaching, out-of-equilibrium boundary layer. In contrast to the perturbation in the separated flow (region B1), which is positive, the perturbation in the reattaching boundary layer (region B2) is negative.
Figure 16 thus shows that as the shock moves downstream, the dynamics of the separation bubble is characterized by structural changes: depending on the location of the shock, the
![]() $u$
perturbation in the separated flow has a different structure involving either two regions of significant perturbation (regions B1 and B2) or four regions (regions A2–A5).
$u$
perturbation in the separated flow has a different structure involving either two regions of significant perturbation (regions B1 and B2) or four regions (regions A2–A5).
These kind of structural changes are also captured by individual DMD modes and do not necessarily require the superposition of several modes, as may be seen by spanwise averaging the pure oscillation based on mode LF3, which was shown in three dimensions in figure 11. Eight phases, which cover a complete cycle of the pure oscillation, are shown in figure 17.

Figure 17. Spanwise average of the pure oscillation shown in figure 11. The field of streamwise velocity
![]() $u$
is shown at eight phase angles: (a) zero, (b)
$u$
is shown at eight phase angles: (a) zero, (b)
![]() $\unicode[STIX]{x03C0}/4$
, (c)
$\unicode[STIX]{x03C0}/4$
, (c)
![]() $\unicode[STIX]{x03C0}/2$
, (d)
$\unicode[STIX]{x03C0}/2$
, (d)
![]() $3\unicode[STIX]{x03C0}/4$
, (e)
$3\unicode[STIX]{x03C0}/4$
, (e)
![]() $\unicode[STIX]{x03C0}$
, (f)
$\unicode[STIX]{x03C0}$
, (f)
![]() $5\unicode[STIX]{x03C0}/4$
, (g)
$5\unicode[STIX]{x03C0}/4$
, (g)
![]() $3\unicode[STIX]{x03C0}/2$
, (h)
$3\unicode[STIX]{x03C0}/2$
, (h)
![]() $7\unicode[STIX]{x03C0}/4$
.
$7\unicode[STIX]{x03C0}/4$
.

Figure 18. Perturbations of the skin-friction coefficient
![]() $C_{f}$
associated with: (a) the low-frequency reconstruction based on modes LF1–LF5 at the phase angle shown in figure 16(c), and (b) the pure oscillation based on mode LF3 at the phase angle shown in figure 17(e). The perturbation of
$C_{f}$
associated with: (a) the low-frequency reconstruction based on modes LF1–LF5 at the phase angle shown in figure 16(c), and (b) the pure oscillation based on mode LF3 at the phase angle shown in figure 17(e). The perturbation of
![]() $C_{f}$
obtained in Priebe & Martín (Reference Priebe and Martín2012) for collapsing bubbles using a conditional analysis of spanwise-averaged and temporally low-pass-filtered DNS fields is also shown.
$C_{f}$
obtained in Priebe & Martín (Reference Priebe and Martín2012) for collapsing bubbles using a conditional analysis of spanwise-averaged and temporally low-pass-filtered DNS fields is also shown.
At zero phase angle (figure 17
a), the same structure as shown in figure 16(a,c), but with reversed sign, is observed. The shock is located downstream of its mean position, i.e. the
![]() $u$
perturbation is positive along the shock. During the sequence shown in figure 17(a–d), the
$u$
perturbation is positive along the shock. During the sequence shown in figure 17(a–d), the
![]() $u$
perturbation along the shock foot decreases and eventually becomes negative, which is consistent with the shock moving upstream. It is clear from the sequence of figures that the velocity perturbations travel tangentially along the shock, from the boundary layer to the free stream. As the shock translates upstream, significant
$u$
perturbation along the shock foot decreases and eventually becomes negative, which is consistent with the shock moving upstream. It is clear from the sequence of figures that the velocity perturbations travel tangentially along the shock, from the boundary layer to the free stream. As the shock translates upstream, significant
![]() $u$
perturbations are visible in the separation bubble and the shear layer. At zero phase angle, the perturbation field shows the previously discussed structure consisting of four distinct regions (referred to as A2–A5 in the discussion of figure 16). During the sequence shown in figure 17(b–d), the two regions of negative perturbation (regions A3 and A4), which are initially of small spatial extent and confined to the proximity of the wall, merge and grow until they fill the entire separation bubble. This behaviour is consistent with a growing bubble. The shock translates upstream until it reaches its most upstream location at a phase angle of
$u$
perturbations are visible in the separation bubble and the shear layer. At zero phase angle, the perturbation field shows the previously discussed structure consisting of four distinct regions (referred to as A2–A5 in the discussion of figure 16). During the sequence shown in figure 17(b–d), the two regions of negative perturbation (regions A3 and A4), which are initially of small spatial extent and confined to the proximity of the wall, merge and grow until they fill the entire separation bubble. This behaviour is consistent with a growing bubble. The shock translates upstream until it reaches its most upstream location at a phase angle of
![]() $\unicode[STIX]{x03C0}$
(see figure 17
e). At this phase angle, the structure in the separation bubble is the same as that observed at zero phase angle, except that the sign is reversed. Most of the bubble is characterized by a negative velocity perturbation as is typical for a large bubble. However, two patches of positive perturbation have appeared near the wall, which is consistent with a weaker-than-average reversed flow. In the sequence shown in figure 17(e–h), these two patches merge and grow until a single region of positive perturbation fills the entire bubble. This behaviour is consistent with a collapsing bubble.
$\unicode[STIX]{x03C0}$
(see figure 17
e). At this phase angle, the structure in the separation bubble is the same as that observed at zero phase angle, except that the sign is reversed. Most of the bubble is characterized by a negative velocity perturbation as is typical for a large bubble. However, two patches of positive perturbation have appeared near the wall, which is consistent with a weaker-than-average reversed flow. In the sequence shown in figure 17(e–h), these two patches merge and grow until a single region of positive perturbation fills the entire bubble. This behaviour is consistent with a collapsing bubble.
The structural changes observed in the velocity perturbation field are also visible in the skin-friction distribution. As is apparent from figure 18, the
![]() $C_{f}$
distributions corresponding to figures 16(c) and 17(e) show three peaks: a negative peak is visible around
$C_{f}$
distributions corresponding to figures 16(c) and 17(e) show three peaks: a negative peak is visible around
![]() $x/\unicode[STIX]{x1D6FF}=-2.5$
. This peak appears to be linked to the region of negative
$x/\unicode[STIX]{x1D6FF}=-2.5$
. This peak appears to be linked to the region of negative
![]() $u$
perturbation along the shock (region A1 in figure 16) and in the shear layer (region A2). Downstream of the negative peak, a positive peak in the
$u$
perturbation along the shock (region A1 in figure 16) and in the shear layer (region A2). Downstream of the negative peak, a positive peak in the
![]() $C_{f}$
distribution is visible around
$C_{f}$
distribution is visible around
![]() $x/\unicode[STIX]{x1D6FF}=-1.25$
. This positive peak is consistent with the first region of positive
$x/\unicode[STIX]{x1D6FF}=-1.25$
. This positive peak is consistent with the first region of positive
![]() $u$
perturbation in the separation bubble (region A3). An additional, less pronounced, positive peak in the
$u$
perturbation in the separation bubble (region A3). An additional, less pronounced, positive peak in the
![]() $C_{f}$
distribution is visible around
$C_{f}$
distribution is visible around
![]() $x/\unicode[STIX]{x1D6FF}=1.0$
. This peak appears to be linked to the second region of positive
$x/\unicode[STIX]{x1D6FF}=1.0$
. This peak appears to be linked to the second region of positive
![]() $u$
perturbation in the separation bubble (region A4).
$u$
perturbation in the separation bubble (region A4).
3.2.2 DMD analysis of the spanwise-averaged DNS flow field
In addition to computing spanwise averages of the 3-D DMD modes, we have also performed a DMD analysis directly on the spanwise-averaged DNS snapshots. Figure 19 provides an overview of the results, which are very similar to those obtained by spanwise averaging the 3-D DMD modes. The DMD spectrum for the spanwise-averaged data is shown in figure 19(a). Consistent with the 3-D spectrum that was shown in figure 4 and discussed in § 3.1, the 2-D spectrum contains several energetic low-frequency modes in the Strouhal number range
![]() $St<0.1$
. The frequencies of the 2-D modes are similar to those that were obtained for the three-dimensional modes. The 2-D mode at
$St<0.1$
. The frequencies of the 2-D modes are similar to those that were obtained for the three-dimensional modes. The 2-D mode at
![]() $St=0.017$
, for example, corresponds to the 3-D mode at
$St=0.017$
, for example, corresponds to the 3-D mode at
![]() $St=0.020$
(LF1). Similarly, the 2-D mode at
$St=0.020$
(LF1). Similarly, the 2-D mode at
![]() $St=0.056$
corresponds to the 3-D mode at
$St=0.056$
corresponds to the 3-D mode at
![]() $St=0.056$
(LF3). In addition to similar frequencies, the mode shapes are also similar. This may be seen by comparing figure 19(b,c), which shows the real and imaginary part of the 2-D mode at
$St=0.056$
(LF3). In addition to similar frequencies, the mode shapes are also similar. This may be seen by comparing figure 19(b,c), which shows the real and imaginary part of the 2-D mode at
![]() $St=0.056$
, to figure 17(e,g), which shows the spanwise-averaged snapshots of the pure oscillation of the corresponding 3-D mode. The similar mode shapes may also be seen by comparing the
$St=0.056$
, to figure 17(e,g), which shows the spanwise-averaged snapshots of the pure oscillation of the corresponding 3-D mode. The similar mode shapes may also be seen by comparing the
![]() $C_{f}$
distribution in figure 19(d) to that associated with the corresponding 3-D mode (figure 18
b).
$C_{f}$
distribution in figure 19(d) to that associated with the corresponding 3-D mode (figure 18
b).

Figure 19. DMD analysis of the spanwise-averaged DNS flow field. The DMD spectrum is shown in (a). The real part of the mode at
![]() $St=0.056$
is shown in (b), the imaginary part in (c) and the
$St=0.056$
is shown in (b), the imaginary part in (c) and the
![]() $C_{f}$
distribution associated with the mode in (d).
$C_{f}$
distribution associated with the mode in (d).
All of the DMD results presented thus far are based either on 3-D data or on spanwise-averaged data. We have also applied the DMD analysis to DNS data on individual streamwise-wall-normal planes. The analysis was repeated for several planes located across the span of the computational domain. While this DMD analysis returns modes at the low frequencies of interest, no clear mode structure could be discerned. The perturbation fields (not shown here) appear less coherent than for the spanwise-averaged data, and the perturbation structure is different from one spanwise location to the next. The inconclusiveness of the DMD analysis based on individual streamwise-wall-normal planes suggests that 3-D effects play a role in the low-frequency dynamics, which is consistent with the 3-D DMD analysis presented in § 3.1.
3.3 DNS on a large domain
We have performed an additional DNS on a larger domain. The spanwise domain size is doubled from
![]() $2\unicode[STIX]{x1D6FF}$
in the baseline simulation to
$2\unicode[STIX]{x1D6FF}$
in the baseline simulation to
![]() $4\unicode[STIX]{x1D6FF}$
in the large domain simulation. The numerics and computational set-up are identical, except that the rescaling is performed as part of the compression-ramp simulation, rather than performing a separate auxiliary simulation. Figure 20 shows four low-pass-filtered (in time) snapshots from the large domain DNS. The same finite-impulse response (FIR) filter that was used to process the separation point signal in figures 1 and 13 is used here to filter the flow field in time.
$4\unicode[STIX]{x1D6FF}$
in the large domain simulation. The numerics and computational set-up are identical, except that the rescaling is performed as part of the compression-ramp simulation, rather than performing a separate auxiliary simulation. Figure 20 shows four low-pass-filtered (in time) snapshots from the large domain DNS. The same finite-impulse response (FIR) filter that was used to process the separation point signal in figures 1 and 13 is used here to filter the flow field in time.

Figure 20. DNS on a
![]() $L_{y}=4\unicode[STIX]{x1D6FF}$
wide domain. Low-pass-filtered (in time) snapshots of the flow are shown, visualized by contours of the streamwise mass flux
$L_{y}=4\unicode[STIX]{x1D6FF}$
wide domain. Low-pass-filtered (in time) snapshots of the flow are shown, visualized by contours of the streamwise mass flux
![]() $\unicode[STIX]{x1D70C}u$
on three planes:
$\unicode[STIX]{x1D70C}u$
on three planes:
![]() $x/\unicode[STIX]{x1D6FF}=-4$
,
$x/\unicode[STIX]{x1D6FF}=-4$
,
![]() $x/\unicode[STIX]{x1D6FF}=0$
and
$x/\unicode[STIX]{x1D6FF}=0$
and
![]() $x/\unicode[STIX]{x1D6FF}=4$
. The four snapshots are distributed over a time of
$x/\unicode[STIX]{x1D6FF}=4$
. The four snapshots are distributed over a time of
![]() $50\unicode[STIX]{x1D6FF}/U_{\infty }$
, which is the length of the DNS after the transients have passed: (a)
$50\unicode[STIX]{x1D6FF}/U_{\infty }$
, which is the length of the DNS after the transients have passed: (a)
![]() $tU_{\infty }/\unicode[STIX]{x1D6FF}=0.0$
, (b)
$tU_{\infty }/\unicode[STIX]{x1D6FF}=0.0$
, (b)
![]() $tU_{\infty }/\unicode[STIX]{x1D6FF}=18.4$
, (c)
$tU_{\infty }/\unicode[STIX]{x1D6FF}=18.4$
, (c)
![]() $tU_{\infty }/\unicode[STIX]{x1D6FF}=28.8$
and (d)
$tU_{\infty }/\unicode[STIX]{x1D6FF}=28.8$
and (d)
![]() $tU_{\infty }/\unicode[STIX]{x1D6FF}=47.2$
.
$tU_{\infty }/\unicode[STIX]{x1D6FF}=47.2$
.
It is apparent from figure 20 that the shock is unsteady at low frequencies: in snapshot (a), the shock is located upstream of its average position, as indicated by the positive momentum perturbation along the shock at
![]() $x/\unicode[STIX]{x1D6FF}=4$
. The shock then moves downstream, which is shown by the slightly negative momentum perturbation at
$x/\unicode[STIX]{x1D6FF}=4$
. The shock then moves downstream, which is shown by the slightly negative momentum perturbation at
![]() $x/\unicode[STIX]{x1D6FF}=4$
in snapshot (b). This is followed by upstream motion: the shock passes through its average position (almost zero perturbation along the shock) in snapshot (c) and is subsequently located upstream of its average position in snapshot (d). It is interesting to note that, in contrast to the baseline DNS, the shock shows signs of three-dimensionalizing in the free stream on the larger domain. It is apparent, especially in figure 20(a,d), that the perturbation along the shock at
$x/\unicode[STIX]{x1D6FF}=4$
in snapshot (b). This is followed by upstream motion: the shock passes through its average position (almost zero perturbation along the shock) in snapshot (c) and is subsequently located upstream of its average position in snapshot (d). It is interesting to note that, in contrast to the baseline DNS, the shock shows signs of three-dimensionalizing in the free stream on the larger domain. It is apparent, especially in figure 20(a,d), that the perturbation along the shock at
![]() $x/\unicode[STIX]{x1D6FF}=4$
varies in intensity along the span rather than remaining uniform.
$x/\unicode[STIX]{x1D6FF}=4$
varies in intensity along the span rather than remaining uniform.
As in the baseline DNS, streamwise-elongated regions of low and high momentum are visible in the downstream flow (see the plane at
![]() $x/\unicode[STIX]{x1D6FF}=4$
in figure 20). The dominant spanwise length scale of the structures is approximately
$x/\unicode[STIX]{x1D6FF}=4$
in figure 20). The dominant spanwise length scale of the structures is approximately
![]() $\unicode[STIX]{x1D6FF}$
. It is apparent from the sequence in figure 20(a–d) that the structures are unsteady at low frequencies as in the baseline DNS: their intensity varies, and it is weaker in snapshots (b,c) than in (a,d). The momentum cores are also unsteady in the wall-normal and spanwise directions: one of the two negative momentum cores is located at
$\unicode[STIX]{x1D6FF}$
. It is apparent from the sequence in figure 20(a–d) that the structures are unsteady at low frequencies as in the baseline DNS: their intensity varies, and it is weaker in snapshots (b,c) than in (a,d). The momentum cores are also unsteady in the wall-normal and spanwise directions: one of the two negative momentum cores is located at
![]() $y/\unicode[STIX]{x1D6FF}\approx 3.5$
in snapshot (a) and at
$y/\unicode[STIX]{x1D6FF}\approx 3.5$
in snapshot (a) and at
![]() $y/\unicode[STIX]{x1D6FF}\approx 4.0$
in snapshot (d), which shows the spanwise motion. One of the positive momentum cores is located at
$y/\unicode[STIX]{x1D6FF}\approx 4.0$
in snapshot (d), which shows the spanwise motion. One of the positive momentum cores is located at
![]() $(z-z_{w})/\unicode[STIX]{x1D6FF}\approx 0.5$
in snapshot (a), and at
$(z-z_{w})/\unicode[STIX]{x1D6FF}\approx 0.5$
in snapshot (a), and at
![]() $(z-z_{w})/\unicode[STIX]{x1D6FF}\approx 0.8$
in snapshot (b), illustrating the wall-normal motion.
$(z-z_{w})/\unicode[STIX]{x1D6FF}\approx 0.8$
in snapshot (b), illustrating the wall-normal motion.
4 Discussion
The 2-D DMD mode shapes described in §§ 3.2.1 and 3.2.2 are consistent with perturbation shapes reported in Priebe & Martín (Reference Priebe and Martín2012) based on a conditional analysis. In Priebe & Martín (Reference Priebe and Martín2012), several DNS of the
![]() $24^{\circ }$
compression-ramp STBLI at Mach 2.9 were analysed, including the simulation used in the present paper. The DNS data were averaged in the spanwise direction and low-pass filtered in time. Based on the resulting 2-D and time-dependent field, it was observed that the structure of the downstream separated flow changes during the low-frequency motions of the shock. The structural changes were described based on the velocity field, the vorticity field, and in terms of the perturbation of the skin-friction coefficient
$24^{\circ }$
compression-ramp STBLI at Mach 2.9 were analysed, including the simulation used in the present paper. The DNS data were averaged in the spanwise direction and low-pass filtered in time. Based on the resulting 2-D and time-dependent field, it was observed that the structure of the downstream separated flow changes during the low-frequency motions of the shock. The structural changes were described based on the velocity field, the vorticity field, and in terms of the perturbation of the skin-friction coefficient
![]() $C_{f}$
through the interaction. Figures 18 and 19(d) show that the
$C_{f}$
through the interaction. Figures 18 and 19(d) show that the
![]() $C_{f}$
perturbation observed in Priebe & Martín (Reference Priebe and Martín2012) is consistent with the DMD mode shape obtained here.
$C_{f}$
perturbation observed in Priebe & Martín (Reference Priebe and Martín2012) is consistent with the DMD mode shape obtained here.
In addition, the present 2-D DMD modes are qualitatively similar to linear instability modes that have been reported in the literature for the reflected shock case. As mentioned in § 1, Touber & Sandham (Reference Touber and Sandham2009) performed a global linear stability analysis of a reflected shock interaction at Mach 2.3. The analysis was based on the mean flow obtained from LES, and an unstable, exponentially growing mode was obtained. The same mode was also found by Pirozzoli et al. (Reference Pirozzoli, Larsson, Nichols, Bernardini, Morgan and Lele2010). The
![]() $C_{f}$
perturbation associated with the linear instability mode is qualitatively similar to the present DMD modes, which may be seen by comparing figure 18 in the present paper to figure 15 in Touber & Sandham (Reference Touber and Sandham2009). In both cases, the
$C_{f}$
perturbation associated with the linear instability mode is qualitatively similar to the present DMD modes, which may be seen by comparing figure 18 in the present paper to figure 15 in Touber & Sandham (Reference Touber and Sandham2009). In both cases, the
![]() $C_{f}$
perturbation shows three dominant local extrema: the first is located upstream of mean separation (at
$C_{f}$
perturbation shows three dominant local extrema: the first is located upstream of mean separation (at
![]() $x/\unicode[STIX]{x1D6FF}\approx -2.5$
in figure 18); the second is located further downstream in the separated flow region (at
$x/\unicode[STIX]{x1D6FF}\approx -2.5$
in figure 18); the second is located further downstream in the separated flow region (at
![]() $x/\unicode[STIX]{x1D6FF}\approx -1.25$
in figure 18) and is of opposite sign compared to the first; and the third extremum, which is also of opposite sign compared to the first, is located near reattachment (at
$x/\unicode[STIX]{x1D6FF}\approx -1.25$
in figure 18) and is of opposite sign compared to the first; and the third extremum, which is also of opposite sign compared to the first, is located near reattachment (at
![]() $x/\unicode[STIX]{x1D6FF}\approx 1.0$
in figure 18).
$x/\unicode[STIX]{x1D6FF}\approx 1.0$
in figure 18).
The similarity between the DMD modes reported here and the linear instability mode reported in the literature is not only confined to wall quantities, such as the skin friction, but also extends into the flow field. This may be seen by comparing the perturbation fields in figures 16, 17 and 19(b,c) in the present paper to the corresponding stability results in the literature (figure 14 in Touber & Sandham (Reference Touber and Sandham2009) and figure 7 in Pirozzoli et al. (Reference Pirozzoli, Larsson, Nichols, Bernardini, Morgan and Lele2010)). A similar structure is observed, consisting of a first region of significant perturbation along the shock (denoted as region A1 in figure 16), a second region of significant perturbation along the separated shear layer (region A2) and two regions in the separated flow (regions A3 and A4), which we recall are of opposite sign compared to the perturbation region in the shear layer. In the stability results, as in the present DMD results, the distinction between regions A3 and A4 is not always clear, and they may also be regarded as a single connected region. Region A5, which is observed in the present results at the corner, is not discernible in the linear stability results reported in the literature. This region could be more pronounced in compression-ramp interactions than in reflected shock interactions due to the presence of the corner.
While our DMD analysis is fundamentally different than a linear stability analysis, the similar shapes of the linear stability modes reported in the literature (Touber & Sandham Reference Touber and Sandham2009; Pirozzoli et al. Reference Pirozzoli, Larsson, Nichols, Bernardini, Morgan and Lele2010) and the DMD modes reported here suggest that the low-frequency dynamics observed in the present STBLI could be due to the saturation of a linear instability in the flow. This would be an interesting dynamical feature that could guide efforts to develop reduced-order models. For instance, in the 2-D flow past a cylinder, the global unstable modes are well known, but the instability mechanism carries the flow to a periodic orbit (vortex shedding) that does not retain any features of the unstable modes (Noack et al. Reference Noack, Afanasiev, Morzyński, Tadmor and Thiele2003). Instead, a different set of global modes dominates the flow field. The nature of this transition from the linear regime to the nonlinear one is present in many reduced-order models of the cylinder flow.
Several works in the literature have found evidence for Görtler-type vortices in STBLIs. Settles et al. (Reference Settles, Fitzpatrick and Bogdonoff1979) performed oil flow visualizations in a
![]() $24^{\circ }$
compression-ramp interaction at Mach 2.85. The oil flow pattern indicated a spanwise variation of the separation length. Settles et al. (Reference Settles, Fitzpatrick and Bogdonoff1979) attributed the spanwise variation to the concave streamline curvature in the interaction leading to the formation of Görtler-type vortices. Loginov et al. (Reference Loginov, Adams and Zheltovodov2006) performed a LES of a
$24^{\circ }$
compression-ramp interaction at Mach 2.85. The oil flow pattern indicated a spanwise variation of the separation length. Settles et al. (Reference Settles, Fitzpatrick and Bogdonoff1979) attributed the spanwise variation to the concave streamline curvature in the interaction leading to the formation of Görtler-type vortices. Loginov et al. (Reference Loginov, Adams and Zheltovodov2006) performed a LES of a
![]() $25^{\circ }$
compression-ramp STBLI at Mach 2.95. They observed streamwise-elongated regions of low and high temperature on the ramp. The spanwise length scale of these structures was approximately
$25^{\circ }$
compression-ramp STBLI at Mach 2.95. They observed streamwise-elongated regions of low and high temperature on the ramp. The spanwise length scale of these structures was approximately
![]() $\unicode[STIX]{x1D6FF}$
, the incoming boundary layer thickness. Loginov et al. (Reference Loginov, Adams and Zheltovodov2006) demonstrated that near separation and reattachment the Görtler number and the streamline curvature were above the critical values in their simulations. As a result, they suggested that the observed flow structures were due to Görtler-type vortices in the interaction.
$\unicode[STIX]{x1D6FF}$
, the incoming boundary layer thickness. Loginov et al. (Reference Loginov, Adams and Zheltovodov2006) demonstrated that near separation and reattachment the Görtler number and the streamline curvature were above the critical values in their simulations. As a result, they suggested that the observed flow structures were due to Görtler-type vortices in the interaction.
Figure 21 shows the streamline curvature
![]() $\unicode[STIX]{x1D6FF}/R$
and the Görtler number
$\unicode[STIX]{x1D6FF}/R$
and the Görtler number
![]() $G_{T}$
along two mean flow streamlines for the present DNS. Streamline 1 passes close to the wall (
$G_{T}$
along two mean flow streamlines for the present DNS. Streamline 1 passes close to the wall (
![]() $z/\unicode[STIX]{x1D6FF}=0.2$
at
$z/\unicode[STIX]{x1D6FF}=0.2$
at
![]() $x/\unicode[STIX]{x1D6FF}=-4.0$
) and streamline 2 passes farther away from the wall (
$x/\unicode[STIX]{x1D6FF}=-4.0$
) and streamline 2 passes farther away from the wall (
![]() $z/\unicode[STIX]{x1D6FF}=0.6$
at
$z/\unicode[STIX]{x1D6FF}=0.6$
at
![]() $x/\unicode[STIX]{x1D6FF}=-4.0$
). The Görtler number is defined as (see Loginov et al.
Reference Loginov, Adams and Zheltovodov2006, Smits & Dussauge Reference Smits and Dussauge2006)
$x/\unicode[STIX]{x1D6FF}=-4.0$
). The Görtler number is defined as (see Loginov et al.
Reference Loginov, Adams and Zheltovodov2006, Smits & Dussauge Reference Smits and Dussauge2006)
where
![]() $R$
is the radius of curvature of the streamline,
$R$
is the radius of curvature of the streamline,
![]() $\unicode[STIX]{x1D6FF}$
is the boundary layer thickness,
$\unicode[STIX]{x1D6FF}$
is the boundary layer thickness,
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
is the boundary layer displacement thickness and
$\unicode[STIX]{x1D6FF}^{\ast }$
is the boundary layer displacement thickness and
![]() $\unicode[STIX]{x1D703}$
is the boundary layer momentum thickness. As is apparent from figure 21, the peak streamline curvature occurs near separation and is
$\unicode[STIX]{x1D703}$
is the boundary layer momentum thickness. As is apparent from figure 21, the peak streamline curvature occurs near separation and is
![]() $\unicode[STIX]{x1D6FF}/R\approx 0.17$
for streamline 1 and
$\unicode[STIX]{x1D6FF}/R\approx 0.17$
for streamline 1 and
![]() $\unicode[STIX]{x1D6FF}/R\approx 0.26$
for streamline 2. The peak Görtler number is
$\unicode[STIX]{x1D6FF}/R\approx 0.26$
for streamline 2. The peak Görtler number is
![]() $G_{T}\approx 1.07$
for streamline 1 and
$G_{T}\approx 1.07$
for streamline 1 and
![]() $G_{T}\approx 1.33$
for streamline 2. Near reattachment, the peak streamline curvature is
$G_{T}\approx 1.33$
for streamline 2. Near reattachment, the peak streamline curvature is
![]() $\unicode[STIX]{x1D6FF}/R\approx 0.075$
for streamline 1 and
$\unicode[STIX]{x1D6FF}/R\approx 0.075$
for streamline 1 and
![]() $\unicode[STIX]{x1D6FF}/R\approx 0.055$
for streamline 2. The peak Görtler number near reattachment is
$\unicode[STIX]{x1D6FF}/R\approx 0.055$
for streamline 2. The peak Görtler number near reattachment is
![]() $G_{T}\approx 0.70$
for streamline 1 and
$G_{T}\approx 0.70$
for streamline 1 and
![]() $G_{T}\approx 0.62$
for streamline 2. According to Smits & Dussauge (Reference Smits and Dussauge2006), the critical value for
$G_{T}\approx 0.62$
for streamline 2. According to Smits & Dussauge (Reference Smits and Dussauge2006), the critical value for
![]() $\unicode[STIX]{x1D6FF}/R$
in Mach
$\unicode[STIX]{x1D6FF}/R$
in Mach
![]() $3$
flow is approximately
$3$
flow is approximately
![]() $0.03$
(under the assumption that Reynolds number effects, which are weak, are ignored). As noted by Loginov et al. (Reference Loginov, Adams and Zheltovodov2006), the critical Görtler number in laminar flow is
$0.03$
(under the assumption that Reynolds number effects, which are weak, are ignored). As noted by Loginov et al. (Reference Loginov, Adams and Zheltovodov2006), the critical Görtler number in laminar flow is
![]() $0.6$
. While the validity of the Görtler stability criterion is unclear in a turbulent and separated flow (Loginov et al.
Reference Loginov, Adams and Zheltovodov2006; Smits & Dussauge Reference Smits and Dussauge2006), the high values of
$0.6$
. While the validity of the Görtler stability criterion is unclear in a turbulent and separated flow (Loginov et al.
Reference Loginov, Adams and Zheltovodov2006; Smits & Dussauge Reference Smits and Dussauge2006), the high values of
![]() $\unicode[STIX]{x1D6FF}/R$
and
$\unicode[STIX]{x1D6FF}/R$
and
![]() $G_{T}$
observed here suggest that the present flow is centrifugally unstable and that Görtler-type vortices provide a likely explanation for the streamwise-elongated regions of low and high momentum that are visible in the 3-D DMD modes.
$G_{T}$
observed here suggest that the present flow is centrifugally unstable and that Görtler-type vortices provide a likely explanation for the streamwise-elongated regions of low and high momentum that are visible in the 3-D DMD modes.
As can be seen from e.g. figures 5, 6, 11, and 12, the spanwise length scale of these regions is approximately
![]() $\unicode[STIX]{x1D6FF}$
, which is in agreement with the value reported in Loginov et al. (Reference Loginov, Adams and Zheltovodov2006). The spanwise wavelength of a pair of momentum perturbation regions is thus
$\unicode[STIX]{x1D6FF}$
, which is in agreement with the value reported in Loginov et al. (Reference Loginov, Adams and Zheltovodov2006). The spanwise wavelength of a pair of momentum perturbation regions is thus
![]() $2\unicode[STIX]{x1D6FF}$
, and this value agrees with the natural spanwise wavelength of streamwise vortex pairs in STBLI flows, which was determined by Schülein & Trofimov (Reference Schülein and Trofimov2011). Using small vortex generators, they artificially introduced disturbances upstream of compression-ramp STBLIs and studied the properties of the streamwise vortices formed in the interaction. They found that streamwise vortices with a natural spanwise wavelength, which is independent of the properties of the upstream forcing, are formed. For compression ramps at Mach 3 and with a ramp angle of
$2\unicode[STIX]{x1D6FF}$
, and this value agrees with the natural spanwise wavelength of streamwise vortex pairs in STBLI flows, which was determined by Schülein & Trofimov (Reference Schülein and Trofimov2011). Using small vortex generators, they artificially introduced disturbances upstream of compression-ramp STBLIs and studied the properties of the streamwise vortices formed in the interaction. They found that streamwise vortices with a natural spanwise wavelength, which is independent of the properties of the upstream forcing, are formed. For compression ramps at Mach 3 and with a ramp angle of
![]() $25^{\circ }$
, i.e. at conditions that are almost identical to those investigated here, the natural spanwise wavelength is close to
$25^{\circ }$
, i.e. at conditions that are almost identical to those investigated here, the natural spanwise wavelength is close to
![]() $2\unicode[STIX]{x1D6FF}$
. Schülein & Trofimov (Reference Schülein and Trofimov2011) found this value to be insensitive to the Reynolds number and to depend on downstream properties such as the ramp angle and interaction strength.
$2\unicode[STIX]{x1D6FF}$
. Schülein & Trofimov (Reference Schülein and Trofimov2011) found this value to be insensitive to the Reynolds number and to depend on downstream properties such as the ramp angle and interaction strength.

Figure 21. Streamline curvature
![]() $\unicode[STIX]{x1D6FF}/R$
and Görtler number
$\unicode[STIX]{x1D6FF}/R$
and Görtler number
![]() $G_{T}$
along two mean flow streamlines: (a,b) streamline 1 passing through
$G_{T}$
along two mean flow streamlines: (a,b) streamline 1 passing through
![]() $x/\unicode[STIX]{x1D6FF}=-4.0$
and
$x/\unicode[STIX]{x1D6FF}=-4.0$
and
![]() $z/\unicode[STIX]{x1D6FF}=0.2$
and (c,d) streamline 2 passing through
$z/\unicode[STIX]{x1D6FF}=0.2$
and (c,d) streamline 2 passing through
![]() $x/\unicode[STIX]{x1D6FF}=-4.0$
and
$x/\unicode[STIX]{x1D6FF}=-4.0$
and
![]() $z/\unicode[STIX]{x1D6FF}=0.6$
.
$z/\unicode[STIX]{x1D6FF}=0.6$
.
It should be noted that in e.g. Settles et al. (Reference Settles, Fitzpatrick and Bogdonoff1979) and Loginov et al. (Reference Loginov, Adams and Zheltovodov2006), the Görtler-type vortices and their effects (such as the spanwise variation of the separation length, and the regions of low and high momentum or temperature) are observed in the time-averaged flow. Loginov et al. (Reference Loginov, Adams and Zheltovodov2006) mention the possibility that these structures could be unsteady. In the present work, we observe unsteady regions of low and high momentum, suggesting that the Görtler-type vortices present in the interaction are unsteady.
Floryan (Reference Floryan1991) reviews experiments of Görtler vortices in low-speed, turbulent flows and describes the following types of unsteady behaviour typically observed:
-
(i) If steady, artificial disturbances are introduced in the incoming boundary layer, the Görtler vortices are visible in the time-averaged flow and tend to be relatively steady about preferred spanwise locations. In the context of STBLIs, examples in this category are the compression-ramp experiments of Schülein & Trofimov (Reference Schülein and Trofimov2011). They place small vortex generators in the incoming boundary layer, leading to a steady spanwise modulation of the inflow.
-
(ii) In the absence of artificial upstream disturbances, the streamwise vortices are often still visible from time-averaged measurements. The reason for this is that even low-amplitude, steady disturbances in the incoming boundary layer, as may be generated by small model roughness or leading edge features, are often sufficient to set preferred locations for the vortices. In STBLIs, as in low-speed flows, most experiments probably fall into this category. The compression-ramp LES of Loginov et al. (Reference Loginov, Adams and Zheltovodov2006) also falls into this category. They observe streamwise structures in the time-averaged flow, which they are able to link to low-amplitude (
 ${\approx}0.03U_{\infty }$
), steady disturbances in their inflow.
${\approx}0.03U_{\infty }$
), steady disturbances in their inflow. -
(iii) In the absence of sufficiently strong and steady disturbances in the inflow, the streamwise vortices do not have any preferred locations. Consequently, they are unsteady and cannot be detected using time-averaged measurement techniques. The dynamics observed in the present work falls into this category. Floryan (Reference Floryan1991) provides additional examples in low-speed turbulent flow. We are not aware of any previous direct observations of unsteady large-scale streamwise structures in STBLIs, although Schülein & Trofimov (Reference Schülein and Trofimov2011) have suggested that such unsteady structures are present in one of their experiments: by polishing the model surface in order to remove small residual roughness at the leading edge and on the model surface, they were able to show that for a very low steady disturbance environment, the streamwise vortices eventually disappear from their surface oil flow visualizations. This behaviour is consistent with the flow transitioning from category (ii) to (iii): the vortices become unsteady when the level of steady disturbances is sufficiently low.
Floryan (Reference Floryan1991) and Schülein & Trofimov (Reference Schülein and Trofimov2011) suggest that when the streamwise structures become unsteady (category (iii)), they still show a dependence on disturbances in the inflow, except that such disturbances will now be predominantly unsteady, rather than steady as in categories (i) and (ii). In order to investigate any possible upstream influence on the streamwise-momentum regions observed here, we have computed the correlation between the streamwise momentum fluctuations upstream of the interaction and those downstream using the low-frequency DMD reconstruction. As is apparent from figure 22, the correlation at zero time lag is
![]() $0.236$
. When considering the correlation with time lag, the maximum value is
$0.236$
. When considering the correlation with time lag, the maximum value is
![]() $0.497$
at a time lag of
$0.497$
at a time lag of
![]() $tU_{\infty }/\unicode[STIX]{x1D6FF}\approx 13.0$
, which corresponds to the turbulent convection time between the two locations considered. Note that by adding additional low-frequency DMD modes and considering e.g. the reconstruction that is based on all of the DMD modes up to a Strouhal number of
$tU_{\infty }/\unicode[STIX]{x1D6FF}\approx 13.0$
, which corresponds to the turbulent convection time between the two locations considered. Note that by adding additional low-frequency DMD modes and considering e.g. the reconstruction that is based on all of the DMD modes up to a Strouhal number of
![]() $St=0.2$
, a very similar peak correlation of
$St=0.2$
, a very similar peak correlation of
![]() $0.475$
at
$0.475$
at
![]() $tU_{\infty }/\unicode[STIX]{x1D6FF}\approx 13.0$
is obtained.
$tU_{\infty }/\unicode[STIX]{x1D6FF}\approx 13.0$
is obtained.

Figure 22. Correlation coefficient
![]() $R$
with time lag
$R$
with time lag
![]() $\unicode[STIX]{x0394}t$
between the streamwise mass flux in the incoming boundary layer and in the downstream flow. The correlation is computed based on the DMD reconstruction that includes only the relevant low-frequency modes (LF1–LF5). The upstream location is at
$\unicode[STIX]{x0394}t$
between the streamwise mass flux in the incoming boundary layer and in the downstream flow. The correlation is computed based on the DMD reconstruction that includes only the relevant low-frequency modes (LF1–LF5). The upstream location is at
![]() $x/\unicode[STIX]{x1D6FF}=-4$
, and the downstream location is at
$x/\unicode[STIX]{x1D6FF}=-4$
, and the downstream location is at
![]() $x/\unicode[STIX]{x1D6FF}=4$
. Both locations lie on the same mean flow streamline, which is chosen to pass through the middle of the log layer in the incoming boundary layer (it passes through
$x/\unicode[STIX]{x1D6FF}=4$
. Both locations lie on the same mean flow streamline, which is chosen to pass through the middle of the log layer in the incoming boundary layer (it passes through
![]() $z/\unicode[STIX]{x1D6FF}=0.2$
, or
$z/\unicode[STIX]{x1D6FF}=0.2$
, or
![]() $z^{+}=70$
, at the upstream location
$z^{+}=70$
, at the upstream location
![]() $x/\unicode[STIX]{x1D6FF}=-4$
).
$x/\unicode[STIX]{x1D6FF}=-4$
).
We thus observe a non-negligible correlation between motions in the upstream boundary layer and the dynamics of the low- and high-momentum regions in the interaction. This observation is consistent with the literature on Görtler vortices, which shows that the underlying centrifugal instability tends to be weak and that some dependence on (steady or unsteady) disturbances in the incoming flow is usually present (Floryan Reference Floryan1991). In addition, this observation may be related to previous works that have shown an upstream influence on the STBLI dynamics (Ganapathisubramani et al. Reference Ganapathisubramani, Clemens and Dolling2007, Reference Ganapathisubramani, Clemens and Dolling2009).
Based on the findings, we propose the following physical mechanism for the low-frequency unsteadiness in supersonic shock wave/turbulent boundary layer interactions: in sufficiently strong interactions, the concave streamline curvature near separation and reattachment leads to a centrifugal instability. Görtler-type vortices are formed in the interaction, which induce the streamwise regions of low and high momentum that are visible in the 3-D DMD modes. The downstream, separated flow is unsteady at low frequencies, since the Görtler-type vortices (and the momentum perturbations that they induce) are unsteady, as is apparent from the DMD analysis. It is this unsteady flow that constitutes the downstream boundary condition for the shock and thereby drives the shock motion. The upstream boundary layer also plays a role. As typically observed in Görtler vortex flows, disturbances in the upstream boundary layer influence the development of the vortices downstream, although we emphasize that the key physics – namely, the concave streamline curvature leading to the formation of Görtler-type vortices – occurs in the downstream flow.
5 Conclusions
The DMD method is applied to a previously reported DNS (Priebe & Martín Reference Priebe and Martín2012) of a Mach 2.9,
![]() $24^{\circ }$
compression-ramp STBLI in order to investigate the low-frequency unsteadiness that is characteristic of this type of flow.
$24^{\circ }$
compression-ramp STBLI in order to investigate the low-frequency unsteadiness that is characteristic of this type of flow.
The analysis is performed on 3-D snapshots of the flow. The DMD spectrum shows several modes in the range of low frequencies of interest (
![]() $St<0.1$
). These low-frequency modes share a similar structure, consisting of streamwise-elongated regions of low- and high-momentum perturbations, which originate at the separation shock foot and extend downstream into the separated flow and further into the reattached flow on the ramp. In addition to these perturbations in the downstream flow, the low-frequency DMD modes show significant perturbations along the shock, which are consistent with streamwise excursions of the shock about its average location.
$St<0.1$
). These low-frequency modes share a similar structure, consisting of streamwise-elongated regions of low- and high-momentum perturbations, which originate at the separation shock foot and extend downstream into the separated flow and further into the reattached flow on the ramp. In addition to these perturbations in the downstream flow, the low-frequency DMD modes show significant perturbations along the shock, which are consistent with streamwise excursions of the shock about its average location.
In order to characterize the unsteadiness captured by the individual DMD modes, the behaviour of the phase angle is investigated. Three distinct types of unsteadiness associated with the streamwise-elongated regions of low and high momentum are observed: these regions move in the spanwise direction, they move in the wall-normal direction and their perturbation strength varies in time. It is also shown that the behaviour of the phase angle along the shock is consistent with perturbations travelling tangentially along the shock, from the shock foot outwards. The unsteadiness captured by the individual DMD modes is further described by computing the pure oscillation based on one of the low-frequency modes and tracking the cores of the low- and high-momentum regions in time.
The reconstruction of the dynamics based on all of the low-frequency DMD modes up to a Strouhal number of
![]() $St=0.1$
accurately captures the low-frequency dynamics seen in the original DNS data. Specifically, the reconstructed separation point signal closely reproduces the low-pass-filtered signal from DNS. The many-mode reconstruction shows a similar flow structure and similar dynamics as the individual DMD modes, in the sense that the unsteadiness of the shock is linked to unsteady regions of low and high momentum in the downstream separated flow.
$St=0.1$
accurately captures the low-frequency dynamics seen in the original DNS data. Specifically, the reconstructed separation point signal closely reproduces the low-pass-filtered signal from DNS. The many-mode reconstruction shows a similar flow structure and similar dynamics as the individual DMD modes, in the sense that the unsteadiness of the shock is linked to unsteady regions of low and high momentum in the downstream separated flow.
We thus conclude that the low-frequency shock unsteadiness in the present STBLI may be represented by the superposition of a number of low-frequency DMD modes, all of which capture unsteady, streamwise-elongated regions of momentum perturbation in the downstream separated flow. Görtler-like vortices, which have been observed in previous STBLI studies in the literature (Settles et al. Reference Settles, Fitzpatrick and Bogdonoff1979; Loginov et al. Reference Loginov, Adams and Zheltovodov2006; Smits & Dussauge Reference Smits and Dussauge2006), provide a likely physical explanation for the presence of the streamwise-elongated regions of low and high momentum. The properties of the streamwise-momentum regions observed here, such as their spanwise wavelength, agree with the values reported in the literature (e.g. Schülein & Trofimov Reference Schülein and Trofimov2011). The fact that the streamwise-momentum regions are found to be unsteady is consistent with the occurrence of unsteady Görtler vortices in low-speed turbulent flows (Floryan Reference Floryan1991); it is also consistent with the observation, reported in Schülein & Trofimov (Reference Schülein and Trofimov2011), that the signature of the Görtler vortices in STBLIs disappears from time-averaged measurements when the level of steady inflow disturbances is reduced to very low values.
Since the 3-D DMD results show that the shock remains essentially two-dimensional and spanwise uniform during the low-frequency motions, we have also investigated the low-frequency dynamics in two dimensions. The spanwise average of the reconstruction based on all of the relevant 3-D modes shows that the separation bubble undergoes structural changes during the low-frequency shock motions. Examples of these structural changes are shown to resemble the structural changes that were previously observed in Priebe & Martín (Reference Priebe and Martín2012) based on a conditional analysis. A qualitative similarity also exists with the linear stability results reported in the literature for the reflected shock case (Touber & Sandham Reference Touber and Sandham2009; Pirozzoli et al. Reference Pirozzoli, Larsson, Nichols, Bernardini, Morgan and Lele2010), which suggests that the low-frequency dynamics could be due to the saturation of a linear instability in the flow.
The 2-D dynamics may also be obtained by applying the DMD method directly to the spanwise-averaged DNS snapshots. This approach is of interest since it is computationally cheaper than performing a 3-D DMD analysis and then spanwise averaging the resulting modes.
Since the time duration captured in the present DNS (approximately
![]() $200\unicode[STIX]{x1D6FF}/U_{\infty }$
) is relatively short compared to the low-frequency phenomenon under investigation, and since this low-frequency phenomenon is broadband, the question arises whether the dynamics observed here is representative of all of the dynamics that would be observed over a much longer time duration, or whether the present dynamics constitutes an ‘unusual event’. Further work on much longer time series is therefore required to investigate the statistical significance over long times of the coherent structures and their unsteadiness observed here. Further work is also required to investigate whether these structures are present and relevant in other STBLI configurations, and how they vary as the flow conditions (the Mach number, the Reynolds number, the wall temperature condition and the shock intensity) are varied.
$200\unicode[STIX]{x1D6FF}/U_{\infty }$
) is relatively short compared to the low-frequency phenomenon under investigation, and since this low-frequency phenomenon is broadband, the question arises whether the dynamics observed here is representative of all of the dynamics that would be observed over a much longer time duration, or whether the present dynamics constitutes an ‘unusual event’. Further work on much longer time series is therefore required to investigate the statistical significance over long times of the coherent structures and their unsteadiness observed here. Further work is also required to investigate whether these structures are present and relevant in other STBLI configurations, and how they vary as the flow conditions (the Mach number, the Reynolds number, the wall temperature condition and the shock intensity) are varied.
Acknowledgements
This work was supported by the Air Force Office of Scientific Research under grant nos AF9550-10-1-0164, AF9550-14-1-0289, and AF9550-15-1-0284. The DNS and DMD computations were performed on the CRoCCo cluster at the University of Maryland Institute for Advanced Computer Studies (UMIACS).
Supplementary movie
A supplementary movie is available at http://dx.doi.org/10.1017/jfm.2016.557.




























