Article contents
Investigation of passive control of the wake past a thick plate by stability and sensitivity analysis of experimental data
Published online by Cambridge University Press: 12 September 2017
Abstract
In this paper we propose a strategy, entirely relying on available experimental data, to estimate the effect of a small control rod on the frequency of vortex shedding in the wake past a thick perforated plate. The considered values of the flow Reynolds number range between 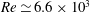 $Re\simeq 6.6\times 10^{3}$ and
$Re\simeq 6.6\times 10^{3}$ and  $Re=5.3\times 10^{4}$. By means of particle image velocimetry, an experimental database consisting of instantaneous flow fields is collected for different values of suction through the body surface. The strategy proposed here is based on classical stability and sensitivity analysis applied to mean flow fields and on the formulation of an original ad hoc model for the mean flow. The mean flow model is obtained by calibrating the closure of the Reynolds averaged Navier–Stokes equations on the basis of the available experimental data through an optimisation algorithm. As a result, it is shown that the predicted control map agrees reasonably well with the equivalent one measured experimentally. Moreover, it is shown that even when turbulence effects are neglected, the stability analysis applied to the mean flow fields provides a reasonable estimation of the vortex shedding frequency, confirming what is known in the literature and extending it up to
$Re=5.3\times 10^{4}$. By means of particle image velocimetry, an experimental database consisting of instantaneous flow fields is collected for different values of suction through the body surface. The strategy proposed here is based on classical stability and sensitivity analysis applied to mean flow fields and on the formulation of an original ad hoc model for the mean flow. The mean flow model is obtained by calibrating the closure of the Reynolds averaged Navier–Stokes equations on the basis of the available experimental data through an optimisation algorithm. As a result, it is shown that the predicted control map agrees reasonably well with the equivalent one measured experimentally. Moreover, it is shown that even when turbulence effects are neglected, the stability analysis applied to the mean flow fields provides a reasonable estimation of the vortex shedding frequency, confirming what is known in the literature and extending it up to 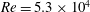 $Re=5.3\times 10^{4}$. It is also shown that, when turbulence is taken into account in the stability analysis using the same closure that is calibrated for the corresponding mean flow model, the prediction of the vortex shedding frequency is systematically improved.
$Re=5.3\times 10^{4}$. It is also shown that, when turbulence is taken into account in the stability analysis using the same closure that is calibrated for the corresponding mean flow model, the prediction of the vortex shedding frequency is systematically improved.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 3
- Cited by





