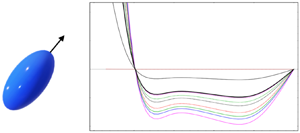
We study the cross-stream inertial migration of a torque-free neutrally buoyant spheroid, of an arbitrary aspect ratio $\kappa$, in wall-bounded plane Poiseuille flow for small particle Reynolds numbers ($Re_p\ll 1$) and confinement ratios ($\lambda \ll 1$), with the channel Reynolds number, $Re_c = Re_p/\lambda ^2$, assumed to be arbitrary; here $\lambda =L/H$, where $L$ is the semi-major axis of the spheroid and $H$ denotes the separation between the channel walls. In the Stokes limit ($Re_p =0)$, and for $\lambda \ll 1$, a spheroid rotates along any of an infinite number of Jeffery orbits parameterized by an orbit constant $C$, while translating with a time-dependent speed along a given ambient streamline. Weak inertial effects stabilize either the spinning ($C=0$) or tumbling orbit ($C=\infty$), or both, depending on $\kappa$. The asymptotic separation of the Jeffery rotation and orbital drift time scales, from that associated with cross-stream migration, implies that migration occurs due to a Jeffery-averaged lift velocity. Although the magnitude of this averaged lift velocity depends on $\kappa$ and $C$, the shape of the lift profiles are identical to those for a sphere, regardless of $Re_c$. In particular, the equilibrium positions for a spheroid remain identical to the classical Segre–Silberberg ones for a sphere, starting off at a distance of about $0.6(H/2)$ from the channel centreline for small $Re_c$, and migrating wallward with increasing $Re_c$. For spheroids with $\kappa \sim O(1)$, the Jeffery-averaged analysis is valid for $Re_p\ll 1$; for extreme aspect ratio spheroids, the regime of validity becomes more restrictive being given by $Re_p \kappa /\ln \kappa \ll 1$ and $Re_p/\kappa \ll 1$ for $\kappa \rightarrow \infty$ (slender fibres) and $\kappa \rightarrow 0$ (flat disks), respectively.