Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-06-24T10:02:24.923Z Has data issue: false hasContentIssue false
  • English
  • Français

Impulsive impact of a twin hull

Published online by Cambridge University Press:  15 March 2024

B.-Y. Ni Open the ORCID record for B.-Y. Ni [Opens in a new window]  and
Y.A. Semenov Open the ORCID record for Y.A. Semenov [Opens in a new window]
B.-Y. Ni
Affiliation:
College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, PR China
Y.A. Semenov*
Affiliation:
College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, PR China
*
†Email address for correspondence: yuriy.a.semenov@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

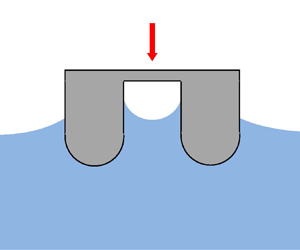
An impulsively starting motion of two cylindrical bodies floating on a free liquid surface is considered. The shape of the cross-section of each body and the distance between them are arbitrary. The integral hodograph method is advanced to derive the complex velocity potential defined in a rectangular parameter region in terms of the elliptic quasi-doubly periodic Jacobi theta functions. A system of singular integral equations in the velocity magnitude on the free surface and in the slope of the wetted part of each body is derived using the kinematic boundary condition, which is then solved numerically. The velocity field, the pressure impulse on the bodies and the added mass coefficients of each body immediately after the impact are determined in a wide range of distances between the bodies and for cross-sectional shapes such as the flat plate and half-circle.

JFM classification

Waves/Free-surface Flows: Wave-structure interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 983 , 25 March 2024 , A16
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chung, J.S. 1977 Forces on submerged cylinders oscillating near a free surface. J. Hydronaut. 11, 100–206.CrossRefGoogle Scholar
Cooker, M.J. & Peregrine, D.H. 1995 Pressure-impulse theory for liquid impact problems. J. Fluid Mech. 297, 193–214.CrossRefGoogle Scholar
Dias, F. & Ghidaglia, J.-M. 2018 Slamming: recent progress in the evaluation of impact pressures. Annu. Rev. Fluid Mech. 50, 243–73.CrossRefGoogle Scholar
Faltinsen, O.M. 2005 Hydrodynamics of High-Speed Marine Vehicles, p. 454. Cambridge University Press.Google Scholar
Faltinsen, O.M., Rognebakke, O. & Timokha, A. 2007 Two-dimensional resonant piston-like sloshing in a moonpool. J. Fluid Mech. 575, 359–397.CrossRefGoogle Scholar
Gurevich, M.I. 1965 Theory of Jets in Ideal Fluids, p. 585. Academic.Google Scholar
Havelock, T.H. 1927 The method of images in some problems of surface waves. Proc. R. Soc. Lond. A 115 (771), 268–280.Google Scholar
Howison, S.D., Ockendon, J.R. & Oliver, J.M. 2004 Oblique slamming, planing and skimming. J. Engng Maths 48, 321–337.CrossRefGoogle Scholar
Iafrati, A. & Korobkin, A.A. 2005 Starting flow generated by the impulsive start of a floating wedge. J. Engng Maths 51, 99–125.CrossRefGoogle Scholar
Joukovskii, N.E. 1890 Modification of Kirchhof's method for determination of a fluid motion in two directions at a fixed velocity given on the unknown streamline. Math. Sbornik. XV (in Russian), 121–278.Google Scholar
von Kármán, T. 1929 The impact of seaplane floats during landing. NACA Tech. Note 321. Washington, DC.Google Scholar
Korobkin, A. & Yilmaz, O. 2009 The initial stage of dam-break flow. J. Engng Maths 63, 293–308.CrossRefGoogle Scholar
Korotkin, A.I. 2009 Added Mass of Ship Structures. Fluid Mech. Appl., vol. 88. Springer.CrossRefGoogle Scholar
Lafeber, W., Brosset, L. & Bogaert, H. 2012 Elementary Loading Processes (ELP) involved in breaking wave impacts: findings from the Sloshel project. In Proceedings of the International Offshore Polar Engineering Conference, 17–22 June, Rhodes, Greece, pp. 265–76.Google Scholar
Lagrange, J.-L. 1781 Mémoire sur la théorie du mouvement des fluides. Nouv. Mém. de l'Acad. Royale des sciences et belles-lettres de Berlin, pp. 695–748.Google Scholar
Michell, J.H. 1890 On the theory of free stream lines. Phil. Trans. R. Soc. Lond. A 181, 389–431.Google Scholar
Milne-Thompson, L.M. 1962 Theoretical Hydrodynamics, 4th edn, p. 657. Macmillan.Google Scholar
Molin, B. 2001 On the piston and sloshing modes in moonpools. J. Fluid Mech. 430, 27–50.CrossRefGoogle Scholar
Semenov, Y.A., Savchenko, Y.N. & Savchenko, G.Y. 2021 Impulsive impact of a submerged body. J. Fluid Mech. 919, R4.CrossRefGoogle Scholar
Semenov, Y.A. & Wu, G.X. 2020 Free-surface gravity flow due to a submerged body in uniform current. J. Fluid Mech. 883, A60.CrossRefGoogle Scholar
Speirs, N.B., Langley, K.R., Pan, Z., Truscott, T.T. & Thoroddsen, S.T. 2021 Cavitation upon low-speed solid-liquid impact. Nat. Commun. 12, 7250.CrossRefGoogle ScholarPubMed
Wagner, H. 1932 Über Stoß und Gleitvorgänge an der Oberfläche von Flüssigkeiten. Z. Angew. Math. Mech. 12, 192–215.CrossRefGoogle Scholar
Whittaker, E.T. & Watson, G.N. 1927 A Course of Modern Analysis, 4th edn. Cambridge University Press.Google Scholar
Yuan, G.Y., Ni, B.Y., Wu, Q.G., Xue, Y.Z. & Han, D.F. 2022 Ice breaking by a high-speed water jet impact. J. Fluid Mech. 934, A1.CrossRefGoogle Scholar
Zhang, A.-M., Li, S.-M., Cui, P., Li, S. & Liu, Y.-L. 2023 A unified theory for bubble dynamics. Phys. Fluids 35, 033323.CrossRefGoogle Scholar