Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-26T17:58:44.618Z Has data issue: false hasContentIssue false
  • English
  • Français

How we compute N matters to estimates of mixing in stratified flows

Published online by Cambridge University Press:  13 October 2017

Robert S. Arthur Open the ORCID record for Robert S. Arthur [Opens in a new window] ,
Subhas K. Venayagamoorthy Open the ORCID record for Subhas K. Venayagamoorthy [Opens in a new window] ,
Jeffrey R. Koseff  and
Oliver B. Fringer
Robert S. Arthur*
Affiliation:
Lawrence Livermore National Laboratory, Livermore, CA 94550, USA
Subhas K. Venayagamoorthy
Affiliation:
Department of Civil and Environmental Engineering, Colorado State University, Fort Collins, CO 80523, USA The Bob and Norma Street Environmental Fluid Mechanics Laboratory, Department of Civil and Environmental Engineering, Stanford University, Stanford, CA 94305, USA
Jeffrey R. Koseff
Affiliation:
The Bob and Norma Street Environmental Fluid Mechanics Laboratory, Department of Civil and Environmental Engineering, Stanford University, Stanford, CA 94305, USA
Oliver B. Fringer
Affiliation:
The Bob and Norma Street Environmental Fluid Mechanics Laboratory, Department of Civil and Environmental Engineering, Stanford University, Stanford, CA 94305, USA
*
†Email address for correspondence: arthur7@llnl.gov
Get access Rights & Permissions [Opens in a new window]

Abstract

Most commonly used models for turbulent mixing in the ocean rely on a background stratification against which turbulence must work to stir the fluid. While this background stratification is typically well defined in idealized numerical models, it is more difficult to capture in observations. Here, a potential discrepancy in ocean mixing estimates due to the chosen calculation of the background stratification is explored using direct numerical simulation data of breaking internal waves on slopes. 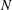Two different methods for computing the buoyancy frequency $N$, one based on a three-dimensionally sorted density field (often used in numerical models) and the other based on locally sorted vertical density profiles (often used in the field), are used to quantify the effect of 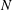$N$ on turbulence quantities. It is shown that how $N$ is calculated changes not only the flux Richardson number 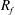$R_{f}$, which is often used to parameterize turbulent mixing, but also the turbulence activity number or the Gibson number 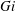$Gi$, leading to potential errors in estimates of the mixing efficiency using 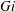$Gi$-based parameterizations.

JFM classification

Geophysical and Geological Flows: Internal waves Turbulent Flows: Stratified turbulence Mixing: Turbulent mixing
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 831 , 25 November 2017 , R2
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arthur, R. S., Koseff, J. R. & Fringer, O. B. 2017 Local versus volume-integrated turbulence and mixing in breaking internal waves on slopes. J. Fluid Mech. 815, 169–198.Google Scholar
Barry, M. E.2002 Mixing in stratified turbulence. PhD thesis, University of Western Australia, Centre for Water Research.Google Scholar
Bouffard, D. & Boegman, L. 2013 A diapycnal diffusivity model for stratified environmental flows. Dyn. Atmos. Oceans 61, 14–34.Google Scholar
Davis, K. A. & Monismith, S. G. 2011 The modification of bottom boundary layer turbulence and mixing by internal waves shoaling on a barrier reef. J. Phys. Oceanogr. 41 (11), 2223–2241.Google Scholar
Dillon, T. M. 1982 Vertical overturns: a comparison of Thorpe and Ozmidov length scales. J. Geophys. Res. 87 (C12), 9601–9613.Google Scholar
Hult, E. L., Troy, C. D. & Koseff, J. R. 2011 The mixing efficiency of interfacial waves breaking at a ridge: 2. Local mixing processes. J. Geophys. Res. 116, C02004.Google Scholar
Ivey, G. N. & Imberger, J. 1991 On the nature of turbulence in a stratified fluid. Part I: the energetics of mixing. J. Phys. Oceanogr. 21 (5), 650–658.2.0.CO;2>CrossRefGoogle Scholar
Ivey, G. N., Winters, K. B. & Koseff, J. R. 2008 Density stratification, turbulence, but how much mixing? Annu. Rev. Fluid Mech. 40, 169–184.Google Scholar
Mater, B. D., Schaad, S. M. & Venayagamoorthy, S. K. 2013 Relevance of the Thorpe length scale in stably stratified turbulence. Phys. Fluids 25, 076604.Google Scholar
Mater, B. D. & Venayagamoorthy, S. K. 2014a The quest for an unambiguous parameterization of mixing efficiency in stably stratified geophysical flows. Geophys. Res. Lett. 41 (13), 4646–4653.Google Scholar
Mater, B. D. & Venayagamoorthy, S. K. 2014b A unifying framework for parameterizing stably stratified shear-flow turbulence. Phys. Fluids 26 (3), 036601.Google Scholar
Monismith, S. G., Koseff, J. R., Walter, R. K., Squibb, M., Pawlak, G., Davis, K. A. & Dunckley, J. 2017 Buoyancy fluxes in stratified flows: observations and parameterizations. J. Phys. Oceanogr. (submitted).Google Scholar
Munk, W. & Wunsch, C. 1998 Abyssal recipes II: energetics of tidal and wind mixing. Deep Sea Res. 45 (12), 1977–2010.Google Scholar
Osborn, T. R. 1980 Estimates of the local rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 10 (1), 83–89.Google Scholar
Osborn, T. R. & Cox, C. S. 1972 Oceanic fine structure. Geophys. Fluid Dyn. 3 (1), 321–345.Google Scholar
Scotti, A. & White, B. 2014 Diagnosing mixing in stratified turbulent flows with a locally defined available potential energy. J. Fluid Mech. 740, 114–135.Google Scholar
Shih, L. H., Koseff, J. R., Ivey, G. N. & Ferziger, J. H. 2005 Parameterization of turbulent fluxes and scales using homogeneous sheared stably stratified turbulence simulations. J. Fluid Mech. 525, 193–214.Google Scholar
Smyth, W. D., Moum, J. N. & Caldwell, D. R. 2001 The efficiency of mixing in turbulent patches: inferences from direct simulations and microstructure observations. J. Phys. Oceanogr. 31 (8), 1969–1992.Google Scholar
Thorpe, S. A. 1977 Turbulence and mixing in a Scottish loch. Phil. Trans. R. Soc. Lond. 286 (1334), 125–181.Google Scholar
Thorpe, S. A. 2005 The Turbulent Ocean. Cambridge University Press.Google Scholar
Venayagamoorthy, S. K. & Koseff, J. R. 2016 On the flux Richardson number in stably stratified turbulence. J. Fluid Mech. 798, R1.Google Scholar
Walter, R. K., Squibb, M. E., Woodson, C. B., Koseff, J. R. & Monismith, S. G. 2014 Stratified turbulence in the nearshore coastal ocean: dynamics and evolution in the presence of internal bores. J. Geophys. Res. 119 (12), 8709–8730.Google Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar
Wunsch, C. & Ferrari, R. 2004 Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36, 281–314.Google Scholar