Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-23T06:49:41.872Z Has data issue: false hasContentIssue false
  • English
  • Français

High-Rayleigh-number convection of a reactive solute in a porous medium

Published online by Cambridge University Press:  04 November 2014

T. J. Ward ,
O. E. Jensen ,
H. Power  and
D. S. Riley
T. J. Ward
Affiliation:
School of Mathematical Sciences, University of Nottingham, University Park, Nottingham NG7 2RD, UK
O. E. Jensen*
Affiliation:
School of Mathematics, University of Manchester, Oxford Road, Manchester M13 9PL, UK
H. Power
Affiliation:
Faculty of Engineering, University of Nottingham, University Park, Nottingham NG7 2RD, UK
D. S. Riley
Affiliation:
School of Mathematical Sciences, University of Nottingham, University Park, Nottingham NG7 2RD, UK
*
†Email address for correspondence: Oliver.Jensen@manchester.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider two-dimensional one-sided convection of a solute in a fluid-saturated porous medium, where the solute decays via a first-order reaction. Fully nonlinear convection is investigated using high-resolution numerical simulations and a low-order model that couples the dynamic boundary layer immediately beneath the distributed solute source to the slender vertical plumes that form beneath. A transient-growth analysis of the boundary layer is used to characterise its excitability. 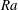Three asymptotic regimes are investigated in the limit of high Rayleigh number $\mathit{Ra}$, in which the domain is considered deep, shallow or of intermediate depth, and for which the Damköhler number 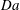$\mathit{Da}$ is respectively large, small or of order unity. Scaling properties of the flow are identified numerically and rationalised via the analytic model. For fully established high-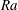$\mathit{Ra}$ convection, analysis and simulation suggest that the time-averaged solute transfer rate scales with 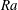$\mathit{Ra}$ and the plume horizontal wavenumber with 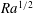$\mathit{Ra}^{1/2}$, with coefficients modulated by 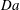$\mathit{Da}$ in each case. For large 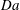$\mathit{Da}$, the rapid reaction rate limits the plume depth and the boundary layer restricts the rate of solute transfer to the bulk, whereas for small 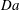$\mathit{Da}$ the average solute transfer rate is ultimately limited by the domain depth and the convection is correspondingly weaker.

JFM classification

Convection: Convection Convection: Convection in porous media Reacting Flows: Reacting Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 760 , 10 December 2014 , pp. 95 - 126
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andres, J. T. H. & Cardoso, S. S. S. 2011 Onset of convection in a porous medium in the presence of chemical reaction. Phys. Rev. E 83, 046312.Google Scholar
Andres, J. T. H. & Cardoso, S. S. S. 2012 Convection and reaction in a diffusive boundary layer in a porous medium: nonlinear dynamics. Chaos 22 (3), 037113.Google Scholar
Asselin, R. 1972 Frequency filter for time integrations. Mon. Weath. Rev. 100 (6), 487–490.Google Scholar
Bestehorn, M. & Firoozabadi, A. 2012 Effect of fluctuations on the onset of density-driven convection in porous media. Phys. Fluids 24, 114102.Google Scholar
Boyd, J. P. 2001 Chebyshev and Fourier Spectral Methods. Dover.Google Scholar
Daniel, D., Tilton, N. & Riaz, A. 2013 Optimal perturbations of gravitationally unstable, transient boundary layers in porous media. J. Fluid Mech. 727, 456–487.Google Scholar
Ennis-King, J. & Paterson, L. 2007 Coupling of geochemical reactions and convective mixing in the long-term geological storage of carbon dioxide. Intl J. Greenh. Gas Control 1, 86–93.Google Scholar
Fu, X., Cueto-Felgueroso, L. & Juanes, R. 2013 Pattern formation and coarsening dynamics in three-dimensional convective mixing in porous media. Phil. Trans. R. Soc. A 371 (2004), 20120355.Google Scholar
Ghesmat, K., Hassanzadeh, H. & Abedi, J. 2009 The impact of geochemistry on convective mixing in a gravitationally unstable diffusive boundary layer in porous media: $\text{CO}_{2}$ storage in saline aquifers. J. Fluid Mech. 673, 480–512.Google Scholar
Graham, M. D. & Steen, P. H. 1994 Plume formation and resonant bifurcations in porous-media convection. J. Fluid Mech. 272, 67–90.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2012 Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett. 108, 224503.CrossRefGoogle Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2013a Convective shutdown in a porous medium at high Rayleigh number. J. Fluid Mech. 719, 551–586.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2013b Stability of columnar convection in a porous medium. J. Fluid Mech. 737, 205–231.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2014 High Rayleigh number convection in a three-dimensional porous medium. J. Fluid Mech. 748, 879–895.Google Scholar
Hidalgo, J. J., Fe, J., Cueto-Felgueroso, L. & Juanes, R. 2012 Scaling of convective mixing in porous media. Phys. Rev. Lett. 109, 264503.CrossRefGoogle ScholarPubMed
Howard, L. N. 1964 Convection at high Rayleigh number. In Applied Mechanics, Proceedings of the 11th Congress of Applied Mechanics (ed. Görtler, H.), pp. 1109–1115. Springer.Google Scholar
Huppert, H. E. & Neufeld, J. A. 2014 The fluid mechanics of carbon dioxide sequestration. Annu. Rev. Fluid Mech. 46, 255–272.Google Scholar
Malkus, W. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225, 196–212.Google Scholar
Mitchell, M. J., Jensen, O. E., Cliffe, K. A. & Maroto-Valer, M. M. 2010 A model of carbon dioxide dissolution and mineral carbonation kinetics. Proc. R. Soc. Lond. A 466, 1265–1290.Google Scholar
Myint, P. C. & Firoozabadi, A. 2013 Onset of buoyancy-driven convection in Cartesian and cylindrical geometries. Phys. Fluids 25 (4), 044105.Google Scholar
Neufeld, J. A., Hesse, M. A., Riaz, A., Hallworth, M. A., Tchelepi, H. A. & Huppert, H. E. 2010 Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 37, L22404.Google Scholar
Otero, J., Dontcheva, L. A., Johnston, H., Worthing, R. A., Kurganov, A., Petrova, G. & Doering, C. R. 2004 High-Rayleigh-number convection in a fluid-saturated porous layer. J. Fluid Mech. 500, 263–281.Google Scholar
Pau, G. S. H., Bell, J. B., Pruess, K., Almgren, A. S., Lijewski, M. J. & Zhang, K. 2010 High-resolution simulation and characterization of density-driven flow in $\text{CO}_{2}$ storage in saline aquifers. Adv. Water Resour. 33, 443–455.Google Scholar
Rapaka, S., Chen, S., Pawar, R. J., Stauffer, P. H. & Zhang, D. 2008 Non-modal growth of perturbations in density-driven convection in porous media. J. Fluid Mech. 609, 285–303.CrossRefGoogle Scholar
Rapaka, S., Pawar, R. J., Stauffer, P. H., Zhang, D. & Chen, S. 2009 Onset of convection over a transient base-state in anisotropic and layered porous media. J. Fluid Mech. 641, 227–244.Google Scholar
Rees, D. A. S., Selim, A. & Ennis-King, J. P. 2008 The instability of unsteady boundary layers in porous media. In Emerging Topics in Heat and Mass Transfer in Porous Media, pp. 85–110. Springer.Google Scholar
Riaz, A., Hesse, M., Tchelepi, H. A. & Orr, F. M. 2006 Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111.CrossRefGoogle Scholar
Ritchie, L. T. & Pritchard, D. 2011 Natural convection and the evolution of a reactive porous medium. J. Fluid Mech. 673, 286–317.Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.Google Scholar
Slim, A. C. 2014 Solutal-convection regimes in a two-dimensional porous medium. J. Fluid Mech. 741, 461–491.Google Scholar
Slim, A. C., Bandi, M. M., Miller, J. C. & Mahadevan, L. 2013 Dissolution-driven convection in a Hele-Shaw cell. Phys. Fluids 25, 024101.Google Scholar
Szulczewski, M. L., Hesse, M. A. & Juanes, R. 2013 Carbon dioxide dissolution in structural and stratigraphic traps. J. Fluid Mech. 736, 287–315.Google Scholar
Tilton, N., Daniel, D. & Riaz, A. 2013 The initial transient period of gravitationally unstable diffusive boundary layers developing in porous media. Phys. Fluids 25 (9), 092107.Google Scholar
Tilton, N. & Riaz, A. 2014 Nonlinear stability of gravitationally unstable, transient, diffusive boundary layers in porous media. J. Fluid Mech. 745, 251–278.Google Scholar
Trefethen, L. N. 2000 Spectral Methods in MATLAB. SIAM.Google Scholar
Ward, T. J., Cliffe, K. A., Jensen, O. E. & Power, H. 2014 Dissolution-driven porous-medium convection in the presence of chemical reaction. J. Fluid Mech. 747, 316–349.CrossRefGoogle Scholar
Wen, B., Chini, G. P., Dianati, N. & Doering, C. R. 2013 Computational approaches to aspect-ratio-dependent upper bounds and heat flux in porous medium convection. Phys. Lett. A 377 (41), 2931–2938.Google Scholar

Ward et al. supplementary movie

Concentration (left) and streamfunction (right) for fully established convection in a deep domain for parameters as given in figure 2 of the main paper.

Download Ward et al. supplementary movie(Video)
Video 10.1 MB

Ward et al. supplementary movie

Concentration (left) and streamfunction (right) for fully established convection in a deep domain for parameters as given in figure 2 of the main paper.

Download Ward et al. supplementary movie(Video)
Video 6 MB