Article contents
Heat transfer across sheared suspensions: role of the shear-induced diffusion
Published online by Cambridge University Press: 29 April 2013
Abstract
Suspensions of non-Brownian spherical particles undergoing shear provide a unique system where mixing occurs spontaneously at low Reynolds numbers. Through a combination of experiments and simulations, we investigate the effect of shear-induced particle diffusion on the transfer of heat across suspensions. The influence of particle size, particle volume fraction and applied shear are examined. By applying a heat pulse to the inner copper wall of a Couette cell and analysing its transient temperature decay, the effective thermal diffusivity of the suspension,  $\alpha $, is obtained. Using index matching and laser-induced fluorescence imaging, we measured individual particle trajectories and calculated their diffusion coefficients. Simulations that combined a lattice Boltzmann technique to solve for the flow and a passive Brownian tracer algorithm to solve for the transfer of heat are in very good agreement with experiments. Fluctuations induced by the presence of particles within the fluid cause a significant enhancement (
$\alpha $, is obtained. Using index matching and laser-induced fluorescence imaging, we measured individual particle trajectories and calculated their diffusion coefficients. Simulations that combined a lattice Boltzmann technique to solve for the flow and a passive Brownian tracer algorithm to solve for the transfer of heat are in very good agreement with experiments. Fluctuations induced by the presence of particles within the fluid cause a significant enhancement (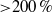 ${\gt }200\hspace{0.167em} \% $) of the suspension transport properties. The effective thermal diffusivity was found to be linear with respect to both the Péclet number (
${\gt }200\hspace{0.167em} \% $) of the suspension transport properties. The effective thermal diffusivity was found to be linear with respect to both the Péclet number (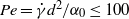 $\mathit{Pe}= \dot {\gamma } {d}^{2} / {\alpha }_{0} \leq 100$) and the solid volume fraction (
$\mathit{Pe}= \dot {\gamma } {d}^{2} / {\alpha }_{0} \leq 100$) and the solid volume fraction (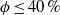 $\phi \leq 40\hspace{0.167em} \% $), leading to a simple correlation
$\phi \leq 40\hspace{0.167em} \% $), leading to a simple correlation 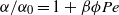 $\alpha / {\alpha }_{0} = 1+ \beta \phi \mathit{Pe}$ where
$\alpha / {\alpha }_{0} = 1+ \beta \phi \mathit{Pe}$ where 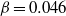 $\beta = 0. 046$ and
$\beta = 0. 046$ and 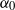 ${\alpha }_{0} $ is the thermal diffusivity of the suspension at rest. In our Couette cell, the enhancement was found to be optimum for a volume fraction,
${\alpha }_{0} $ is the thermal diffusivity of the suspension at rest. In our Couette cell, the enhancement was found to be optimum for a volume fraction, 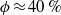 $\phi \approx 40\hspace{0.167em} \% $, above which, due to steric effects, both the particle diffusion motion and of the effective thermal diffusion dramatically decrease. No such correlation was found between the average particle rotation and the thermal diffusivity of the suspension, suggesting that the driving mechanism for enhanced transport is the translational particle diffusivity. Movies are available with the online version of the paper.
$\phi \approx 40\hspace{0.167em} \% $, above which, due to steric effects, both the particle diffusion motion and of the effective thermal diffusion dramatically decrease. No such correlation was found between the average particle rotation and the thermal diffusivity of the suspension, suggesting that the driving mechanism for enhanced transport is the translational particle diffusivity. Movies are available with the online version of the paper.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 44
- Cited by




