Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-26T16:04:26.129Z Has data issue: false hasContentIssue false
  • English
  • Français

The generation of gravity–capillary solitary waves by a pressure source moving at a trans-critical speed

Published online by Cambridge University Press:  01 December 2016

Naeem Masnadi  and
James H. Duncan
Naeem Masnadi
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
James H. Duncan*
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
*
†Email address for correspondence: duncan@umd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The unsteady response of a water free surface to a localized pressure source moving at constant speed 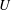$U$ in the range 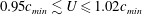$0.95c_{min}\lesssim U\leqslant 1.02c_{min}$, where 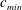$c_{min}$ is the minimum phase speed of linear gravity–capillary waves in deep water, is investigated through experiments and numerical simulations. This unsteady response state, which consists of a V-shaped pattern behind the source, and features periodic shedding of pairs of depressions from the tips of the V, was first observed qualitatively by Diorio et al. (Phys. Rev. Lett., vol. 103, 2009, 214502) and called state III. In the present investigation, cinematic shadowgraph and refraction-based techniques are utilized to measure the temporal evolution of the free-surface deformation pattern downstream of the source as it moves along a towing tank, while numerical simulations of the model equation described by Cho et al. (J. Fluid Mech., vol. 672, 2011, pp. 288–306) are used to extend the experimental results over longer times than are possible in the experiments. From the experiments, it is found that the speed–amplitude characteristics and the shape of the depressions are nearly the same as those of the freely propagating gravity–capillary lumps of inviscid potential theory. The decay rate of the depressions is measured from their height–time characteristics, which are well fitted by an exponential decay law with an order one decay constant. It is found that the shedding period of the depression pairs decreases with increasing source strength and speed. As the source speed approaches 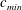$c_{min}$, this period tends to approximately 1 s for all source magnitudes. At the low-speed boundary of state III, a new response with unsteady asymmetric shedding of depressions is found. This response is also predicted by the model equation.

JFM classification

Waves/Free-surface Flows: Capillary waves Waves/Free-surface Flows: Solitary waves Waves/Free-surface Flows: Surface gravity waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 810 , 10 January 2017 , pp. 448 - 474
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. & Westerweel, J. 2010 Particle Image Velocimetry, 1st edn. Cambridge University Press.Google Scholar
Akers, B. & Milewski, P. A. 2009 A model equation for wavepacket solitary waves arising from capillary-gravity flows. Stud. Appl. Maths 122 (3), 249–274.CrossRefGoogle Scholar
Akers, B. & Milewski, P. A. 2010 Dynamics of three-dimensional gravity–capillary solitary waves in deep water. SIAM J. Appl. Maths 70 (7), 2390–2408.CrossRefGoogle Scholar
Akylas, T. R. 1984 On the excitation of long nonlinear water waves by a moving pressure distribution. J. Fluid Mech. 141, 455–466.CrossRefGoogle Scholar
Akylas, T. R. 1993 Envelope solitons with stationary crests. Phys. Fluids A 5 (4), 789–791.CrossRefGoogle Scholar
Akylas, T. R. & Cho, Y. 2008 On the stability of lumps and wave collapse in water waves. Phil. Trans. R. Soc. Lond. A 366 (1876), 2761–2774.Google ScholarPubMed
Amini, A. A., Weymouth, T. E. & Jain, R. C. 1990 Using dynamic programming for solving variational problems in vision. IEEE Trans. Pattern Anal. Mach. Intell. 12 (9), 855–867.CrossRefGoogle Scholar
Berger, K. M. & Milewski, P. A. 2000 The generation and evolution of lump solitary waves in surface-tension-dominated flows. SIAM J. Appl. Maths 61 (3), 731–750.CrossRefGoogle Scholar
Cho, Y.2010 Nonlinear dynamics of three-dimensional solitary waves. PhD thesis, Massachusetts Institute of Technology.Google Scholar
Cho, Y., Diorio, J. D., Akylas, T. R. & Duncan, J. H. 2011 Resonantly forced gravity–capillary lumps on deep water. Part 2. Theoretical model. J. Fluid Mech. 672, 288–306.CrossRefGoogle Scholar
Dias, F. & Kharif, C. 1999 Nonlinear gravity and capillary-gravity waves. Annu. Rev. Fluid Mech. 31 (1), 301–346.CrossRefGoogle Scholar
Diorio, J., Cho, Y., Duncan, J. H. & Akylas, T. R. 2009 Gravity–capillary lumps generated by a moving pressure source. Phys. Rev. Lett. 103, 214502.CrossRefGoogle ScholarPubMed
Diorio, J. D., Cho, Y., Duncan, J. H. & Akylas, T. R. 2011 Resonantly forced gravity–capillary lumps on deep water. Part 1. Experiments. J. Fluid Mech. 672, 268–287.CrossRefGoogle Scholar
Duncan, J. H., Qiao, H., Philomin, V. & Wenz, A. 1999 Gentle spilling breakers: crest profile evolution. J. Fluid Mech. 379, 191–222.CrossRefGoogle Scholar
Falcon, É., Laroche, C. & Fauve, S. 2002 Observation of depression solitary surface waves on a thin fluid layer. Phys. Rev. Lett. 89, 204501.CrossRefGoogle ScholarPubMed
Kass, M., Witkin, A. & Terzopoulos, D. 1988 Snakes: active contour models. Intl J. Comput. Vis. 1 (4), 321–331.CrossRefGoogle Scholar
Kim, B. & Akylas, T. R. 2005 On gravity–capillary lumps. J. Fluid Mech. 540, 337–351.CrossRefGoogle Scholar
Korteweg, D. J. & de Vries, G. 1895 On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Phil. Mag. 39 (240), 422–443.CrossRefGoogle Scholar
Lee, S.-J., Yates, G. T. & Wu, T. Y. 1989 Experiments and analyses of upstream-advancing solitary waves generated by moving disturbances. J. Fluid Mech. 199, 569–593.CrossRefGoogle Scholar
Longuet-Higgins, M. S. 1989 Capillary-gravity waves of solitary type on deep water. J. Fluid Mech. 200, 451–470.CrossRefGoogle Scholar
Longuet-Higgins, M. S. 1993 Capillary-gravity waves of solitary type and envelope solitons on deep water. J. Fluid Mech. 252, 703–711.CrossRefGoogle Scholar
Longuet-Higgins, M. S. & Zhang, X. 1997 Experiments on capillary-gravity waves of solitary type on deep water. Phys. Fluids 9 (7), 1963–1968.CrossRefGoogle Scholar
Milewski, P. A. 2005 Three-dimensional localized solitary gravity–capillary waves. Commun. Math. Sci. 3 (1), 89–99.CrossRefGoogle Scholar
Moisy, F., Rabaud, M. & Salsac, K. 2009 A synthetic schlieren method for the measurement of the topography of a liquid interface. Exp. Fluids 46 (6), 1021–1036.CrossRefGoogle Scholar
Părău, E. I., Vanden-Broeck, J.-M. & Cooker, M. J. 2005 Nonlinear three-dimensional gravity–capillary solitary waves. J. Fluid Mech. 536, 99–105.CrossRefGoogle Scholar
Părău, E. I., Vanden-Broeck, J.-M. & Cooker, M. J. 2007 Three-dimensional capillary-gravity waves generated by a moving disturbance. Phys. Fluids 19 (8), 082102.CrossRefGoogle Scholar
Russell, J. S. 1844 Reports on waves. In Report of the Fourteenth Meeting of the British Association for the Advancement of Science, pp. 311–390.Google Scholar
Wang, Z. & Milewski, P. A. 2012 Dynamics of gravity–capillary solitary waves in deep water. J. Fluid Mech. 708, 480–501.CrossRefGoogle Scholar
Wu, T. Y. 1987 Generation of upstream advancing solitons by moving disturbances. J. Fluid Mech. 184, 75–99.CrossRefGoogle Scholar
Zhang, X. 1995 Capillary-gravity and capillary waves generated in a wind wave tank: observations and theories. J. Fluid Mech. 289, 51–82.CrossRefGoogle Scholar