Article contents
Fluid–structure interaction of a square cylinder at different angles of attack
Published online by Cambridge University Press: 23 April 2014
Abstract
This study investigates the free transverse flow-induced vibration (FIV) of an elastically mounted low-mass-ratio square cylinder in a free stream, at three different incidence angles: 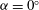 ${{\alpha }}=0^\circ $,
${{\alpha }}=0^\circ $, 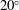 $20^\circ $ and
$20^\circ $ and 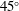 $45^\circ $. This geometric setup presents a body with an angle of attack, sharp corners and some afterbody, and therefore is a generic body that can be used to investigate a wide range of FIV phenomena. A recent study by Nemes et al. (J. Fluid Mech., vol. 710, 2012, pp. 102–130) provided a broad overview of the flow regimes present as a function of both the angle of attack
$45^\circ $. This geometric setup presents a body with an angle of attack, sharp corners and some afterbody, and therefore is a generic body that can be used to investigate a wide range of FIV phenomena. A recent study by Nemes et al. (J. Fluid Mech., vol. 710, 2012, pp. 102–130) provided a broad overview of the flow regimes present as a function of both the angle of attack  ${{\alpha }}$ and reduced flow velocity
${{\alpha }}$ and reduced flow velocity 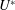 ${U^{*}}$. Here, the focus is on the three aforementioned representative angles of attack:
${U^{*}}$. Here, the focus is on the three aforementioned representative angles of attack: 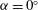 ${{\alpha }}=0^\circ $, where the FIV is dominated by transverse galloping;
${{\alpha }}=0^\circ $, where the FIV is dominated by transverse galloping; 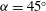 ${{\alpha }}=45^\circ $, where the FIV is dominated by vortex-induced vibration (VIV); and an intermediate value of
${{\alpha }}=45^\circ $, where the FIV is dominated by vortex-induced vibration (VIV); and an intermediate value of 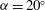 ${{\alpha }}=20^\circ $, where the underlying FIV phenomenon has previously been difficult to determine. For the
${{\alpha }}=20^\circ $, where the underlying FIV phenomenon has previously been difficult to determine. For the 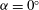 ${{\alpha }}=0^\circ $ case, the amplitude of oscillation increases linearly with the flow speed except for a series of regimes that occur when the vortex shedding frequency is in the vicinity of an odd-integer multiple of the galloping oscillation frequency, and the vortex shedding synchronizes to this multiple of the oscillation frequency. It is shown that only odd-integer multiple synchronizations should occur. These synchronizations explain the ‘kinks’ in the galloping amplitude response for light bodies first observed by Bearman et al. (J. Fluids Struct., vol. 1, 1987, pp. 19–34). For the
${{\alpha }}=0^\circ $ case, the amplitude of oscillation increases linearly with the flow speed except for a series of regimes that occur when the vortex shedding frequency is in the vicinity of an odd-integer multiple of the galloping oscillation frequency, and the vortex shedding synchronizes to this multiple of the oscillation frequency. It is shown that only odd-integer multiple synchronizations should occur. These synchronizations explain the ‘kinks’ in the galloping amplitude response for light bodies first observed by Bearman et al. (J. Fluids Struct., vol. 1, 1987, pp. 19–34). For the 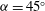 ${{\alpha }}=45^\circ $ case, the VIV response consists of a number of subtle, but distinctly different regimes, with five regimes of high-amplitude oscillations, compared to two found in the classic VIV studies of a circular cylinder. For the intermediate
${{\alpha }}=45^\circ $ case, the VIV response consists of a number of subtle, but distinctly different regimes, with five regimes of high-amplitude oscillations, compared to two found in the classic VIV studies of a circular cylinder. For the intermediate 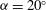 ${{\alpha }}=20^\circ $ case, a typical VIV ‘upper branch’ occurs followed by a ‘higher branch’ of very large-amplitude response. The higher branch is caused by a subharmonic synchronization between the vortex shedding and the body oscillation frequency, where two cycles of vortex shedding occur over one cycle of oscillation. It appears that this subharmonic synchronization is a direct result of the asymmetric body. Overall, the FIV of the square cylinder is shown to be very rich, with a number of distinct regimes, controlled by both
${{\alpha }}=20^\circ $ case, a typical VIV ‘upper branch’ occurs followed by a ‘higher branch’ of very large-amplitude response. The higher branch is caused by a subharmonic synchronization between the vortex shedding and the body oscillation frequency, where two cycles of vortex shedding occur over one cycle of oscillation. It appears that this subharmonic synchronization is a direct result of the asymmetric body. Overall, the FIV of the square cylinder is shown to be very rich, with a number of distinct regimes, controlled by both  ${{\alpha }}$ and
${{\alpha }}$ and 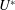 ${U^{*}}$. Importantly,
${U^{*}}$. Importantly,  ${{\alpha }}$ controls the underlying FIV phenomenon, as well as controlling the types of possible synchronization between the oscillation and vortex shedding.
${{\alpha }}$ controls the underlying FIV phenomenon, as well as controlling the types of possible synchronization between the oscillation and vortex shedding.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 174
- Cited by




