Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tian, Xinliang
Hu, Zhihuan
Lu, Haining
and
Yang, Jianmin
2017.
Direct numerical simulations on the flow past an inclined circular disk.
Journal of Fluids and Structures,
Vol. 72,
Issue. ,
p.
152.
Liu, Lei
Yang, Jian-min
Lyu, Hai-ning
Tian, Xin-liang
and
Peng, Tao
2018.
Effects of Degrees of Motion Freedom on Free-Fall of A Sphere in Fluid.
China Ocean Engineering,
Vol. 32,
Issue. 5,
p.
605.
Farrugia, Russell
Portelli, Barnaby
Grech, Ivan
Camilleri, Duncan
Casha, Owen
Micallef, Joseph
and
Gatt, Edward
2018.
Air damping analysis in resonating micro-mirrors.
p.
1.
Gao, Song
Tao, Longbin
Tian, Xinliang
and
Yang, Jianmin
2018.
Flow around an inclined circular disk.
Journal of Fluid Mechanics,
Vol. 851,
Issue. ,
p.
687.
Farrugia, Russell
Grech, Ivan
Camilleri, Duncan
Micallef, Joseph
Casha, Owen
and
Gatt, Edward
2019.
CFD Analysis of Aerodynamic Drag on Resonating MEMS Micro-Scanners.
p.
1.
Liu, Lei
Yang, Jianmin
Lu, Haining
Tian, Xinliang
and
Lu, Wenyue
2019.
Numerical simulations on the motion of a heavy sphere in upward Poiseuille flow.
Ocean Engineering,
Vol. 172,
Issue. ,
p.
245.
Cong, Long-fei
and
Teng, Bin
2019.
Hydrodynamic Characteristics of Square Heaving Plates with Opening Under Forced Oscillation.
China Ocean Engineering,
Vol. 33,
Issue. 6,
p.
637.
Bezunartea-Barrio, Ana
Fernandez-Ruano, Sergio
Maron-Loureiro, Adolfo
Molinelli-Fernandez, Enrique
Moreno-Buron, Francisco
Oria-Escudero, Julio
Rios-Tubio, José
Soriano-Gomez, Cristina
Valea-Peces, Alvaro
Lopez-Pavon, Carlos
and
Souto-Iglesias, Antonio
2020.
Scale Effects on Heave Plates for Semi-Submersible Floating Offshore Wind Turbines: Case Study With a Solid Plain Plate.
Journal of Offshore Mechanics and Arctic Engineering,
Vol. 142,
Issue. 3,
Wu, Xia
Zhang, Xiantao
Tian, Xinliang
Li, Xin
and
Lu, Wenyue
2020.
A review on fluid dynamics of flapping foils.
Ocean Engineering,
Vol. 195,
Issue. ,
p.
106712.
Dorschner, Benedikt
and
Colonius, Tim
2020.
Immersed Boundary Method.
p.
3.
Zhao, Yakun
Gao, Song
Zhang, Xiantao
Guo, Xiaoxian
Li, Xin
and
Tian, Xinliang
2021.
Direct numerical simulations on the flow past a thin square plate.
Physics of Fluids,
Vol. 33,
Issue. 3,
Farrugia, Russell
Portelli, Barnaby
Grech, Ivan
Camilleri, Duncan
Casha, Owen
Micallef, Joseph
and
Gatt, Edward
2022.
Air damping of high performance resonating micro-mirrors with angular vertical comb-drive actuators.
Microsystem Technologies,
Vol. 28,
Issue. 6,
p.
1451.
Bi, Dianfang
Sun, Tiezhi
Wei, Yingjie
and
Huang, Xudong
2022.
On the dynamic behaviors of freely falling annular disks at different Reynolds numbers.
Physics of Fluids,
Vol. 34,
Issue. 4,
Bi, Dianfang
Lu, Jiaxing
Wei, Yingjie
and
Sun, Tiezhi
2022.
Numerical analysis of factors influencing freely falling annular disks in an infinite fluid.
Physical Review Fluids,
Vol. 7,
Issue. 5,
Medina-Manuel, Antonio
Botia-Vera, Elkin
Saettone, Simone
Calderon-Sanchez, Javier
Bulian, Gabriele
and
Souto-Iglesias, Antonio
2022.
Hydrodynamic coefficients from forced and decay heave motion tests of a scaled model of a column of a floating wind turbine equipped with a heave plate.
Ocean Engineering,
Vol. 252,
Issue. ,
p.
110985.
Ouyang, Danxue
Tian, Xinliang
Zhao, Yakun
Wen, Binrong
Li, Xin
Li, Jun
Peng, Tao
and
Peng, Zhike
2022.
Wake transitions behind a streamwise rotating disk.
Journal of Fluid Mechanics,
Vol. 953,
Issue. ,
Liu, Yun
Jojo-Cunningham, Yasmeen
and
Zeytinoglu, Nuri
2024.
Proceedings of the IUTAM Symposium on Turbulent Structure and Particles-Turbulence Interaction.
Vol. 41,
Issue. ,
p.
250.
Wei, Li
Guo, Xiaoxian
Tian, Xinliang
and
Zhao, Yakun
2024.
Three-dimensional autoencoder for the flow field reconstruction of an inclined circular disk.
Ocean Engineering,
Vol. 299,
Issue. ,
p.
117284.
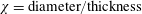 $\unicode[STIX]{x1D712}=\text{diameter}/\text{thickness}$) of the disk is 10. The Reynolds number (
$\unicode[STIX]{x1D712}=\text{diameter}/\text{thickness}$) of the disk is 10. The Reynolds number (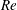 $\mathit{Re}$), based on the maximum speed and the diameter of the disk, is in the range of
$\mathit{Re}$), based on the maximum speed and the diameter of the disk, is in the range of 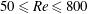 $50\leqslant \mathit{Re}\leqslant 800$. The Keulegan–Carpenter number (
$50\leqslant \mathit{Re}\leqslant 800$. The Keulegan–Carpenter number (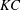 $KC$) is in the range of
$KC$) is in the range of 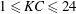 $1\leqslant KC\leqslant 24$. Five flow regimes are observed in the considered
$1\leqslant KC\leqslant 24$. Five flow regimes are observed in the considered 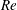 $\mathit{Re}$–
$\mathit{Re}$–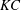 $KC$ space: (I) axisymmetric flow (AS), (II) planar symmetric flow in the low-
$KC$ space: (I) axisymmetric flow (AS), (II) planar symmetric flow in the low-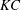 $KC$ region (PSL), (III) azimuthally rotating flow in the low-
$KC$ region (PSL), (III) azimuthally rotating flow in the low-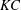 $KC$ region (ARL), (IV) planar symmetric flow in the high-
$KC$ region (ARL), (IV) planar symmetric flow in the high-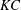 $KC$ region (PSH) and (V) azimuthally rotating flow in the high-
$KC$ region (PSH) and (V) azimuthally rotating flow in the high-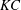 $KC$ region (ARH). The critical boundaries between different flow regimes are identified based on the evolutions of the magnitude and direction of transverse force acting on the disk. For the non-axisymmetric flow regimes, the flow is one-sided with respect to the axis of the disk and is associated with a non-zero mean value of the transverse force acting on the disk.
$KC$ region (ARH). The critical boundaries between different flow regimes are identified based on the evolutions of the magnitude and direction of transverse force acting on the disk. For the non-axisymmetric flow regimes, the flow is one-sided with respect to the axis of the disk and is associated with a non-zero mean value of the transverse force acting on the disk.




