Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-24T16:31:18.232Z Has data issue: false hasContentIssue false
  • English
  • Français

A falling film down a slippery inclined plane

Published online by Cambridge University Press:  07 September 2011

A. Samanta ,
C. Ruyer-Quil  and
B. Goyeau
A. Samanta
Affiliation:
Laboratoire FAST, UMR CNRS 7608, Université Pierre et Marie Curie, Campus Universitaire, 91405 Orsay, France
C. Ruyer-Quil*
Affiliation:
Laboratoire FAST, UMR CNRS 7608, Université Pierre et Marie Curie, Campus Universitaire, 91405 Orsay, France
B. Goyeau
Affiliation:
Laboratoire EM2C, UPR CNRS 288, École Centrale Paris, Grande Voie des Vignes, 92295 Châtenay-Malabry CEDEX, France
*
†Email address for correspondence: ruyer@fast.u-psud.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

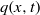A gravity-driven film flow on a slippery inclined plane is considered within the framework of long-wave and boundary layer approximations. Two coupled depth-averaged equations are derived in terms of the local flow rate and the film thickness 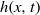. Linear stability analysis of the averaged equations shows good agreement with the Orr–Sommerfeld analysis. The effect of a slip at the wall on the primary instability has been found to be non-trivial. Close to the instability onset, the effect is destabilising whereas it becomes stabilising at larger values of the Reynolds number. Nonlinear travelling waves are amplified by the presence of the slip. Comparisons to direct numerical simulations show a remarkable agreement for all tested values of parameters. The averaged equations capture satisfactorily the speed, shape and velocity distribution in the waves. The Navier slip condition is observed to significantly enhance the backflow phenomenon in the capillary region of the solitary waves with a possible effect on heat and mass transfer.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models Waves/Free-surface Flows: Solitary waves Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 684 , 10 October 2011 , pp. 353 - 383
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Alekseenko, S. V., Nakoryakov, V. Y. & Pokusaev, B. G. 1985 Wave formation on a vertical falling liquid film. AIChE J. 31, 1446–1460.CrossRefGoogle Scholar
2. Alekseenko, S. V., Nakoryakov, V. E. & Pokusaev, B. G. 1994 Wave Flow in Liquid Films, 3rd edn. Begell House.CrossRefGoogle Scholar
3. Beavers, G. S. & Joseph, D. D. 1967 Boundary conditions at a naturally permeable wall. J. Fluid Mech. 30, 197–207.CrossRefGoogle Scholar
4. Benney, D. J. 1966 Long waves on liquid films. J. Math. Phys. 45, 150–155.CrossRefGoogle Scholar
5. Blake, T. D. 1990 Slip between a liquid and a solid: D. M. Tolstoi’s (1952) theory reconsidered. Colloids Surf. 47, 135–145.CrossRefGoogle Scholar
6. Chang, H. C. & Demekhin, E. A. 2002 Complex Wave Dynamics on Thin Films, 1st edn. Elsevier.Google Scholar
7. Chang, H.-C., Demekhin, E. A. & Kopelevitch, D. I. 1993 Nonlinear evolution of waves on a vertically falling film. J. Fluid Mech. 250, 433–480.CrossRefGoogle Scholar
8. Dietze, G. F., AL-Sibai, F. & Kneer, R. 2009 Experimental study of flow separation in laminar falling liquid films. J. Fluid Mech. 637, 73–104.CrossRefGoogle Scholar
9. Dietze, G. F. & Kneer, R. 2010 Capillary flow separation in 2- and 3-dimensional laminar falling liquid films. In Proc. 14th Intl Heat Transfer Conf., pp. IHTC14–22064, ISBN 978-0-7918-3879-2.Google Scholar
10. Dietze, G. F., Leefken, A. & Kneer, R. 2008 Investigation of the backflow phenomenon in falling liquid films. J. Fluid Mech. 595, 435–459.CrossRefGoogle Scholar
11. Doedel, E. J., Champneys, A. R., Fairgrieve, T. F., Kuznetsov, Y. A., Sandstede, B. & Wang, X.-J. 2007 Auto07: Continuation and bifurcation software for ordinary differential equations. Tech Rep. Department of Computer Science, Concordia University, Montreal, Canada (Available by FTP from ftp.cs.concordia.ca in directory pub/doedel/auto).Google Scholar
12. Germain, P. 1973 Cours de Mécanique des Milieux Continus. Masson.Google Scholar
13. Goyeau, B., Lhuillier, D., Gobin, D. & Velarde, M. G. 2003 Momentum transport at a fluid-porous interface. Intl J. Heat Mass Transfer 46, 4071–4081.CrossRefGoogle Scholar
14. Kapitza, P. L. 1948 Wave flow of thin layers of a viscous fluid: I. Free flow – II. Fluid flow in the presence of continuous gas flow and heat transfer. In Collected Papers of P. L. Kapitza (1965) (ed. Haar, D. T. ). pp. 662–689. Pergamon. (Original paper in Russian: Zh. Ekper. Teor. Fiz. 18, I. 3–18, II. 19–28).Google Scholar
15. Kelly, R. E., Goussis, D. A., Lin, S. P. & Hsu, F. K. 1989 The mechanism for surface wave instability in film flow down an inclined plane. Phys. Fluids A 1, 819–828.CrossRefGoogle Scholar
16. Kunugi, T. & Kino, C. 2005 DNS of falling film structure and heat transfer via mars method. Comput. Struct. 83, 455–462.CrossRefGoogle Scholar
17. Liu, J. & Gollub, J. P. 1994 Solitary wave dynamics of film flows. Phys. Fluids 6, 1702–1712.CrossRefGoogle Scholar
18. Liu, J., Schneider, B. & Gollub, J. P. 1995 Solitary wave dynamics of film flows. Phys. Fluids 7, 55–67.CrossRefGoogle Scholar
19. Malamataris, N. A., Vlachogiannis, M. & Bontozoglou, V. 2002 Solitary waves on inclined films: flow structure and binary interactions. Phys. Fluids 14 (3), 1082–1094.CrossRefGoogle Scholar
20. Nakaya, C. 1975 Long waves on thin fluid layer flowing down a inclined plane. Phys. Fluids 18, 1407–1412.CrossRefGoogle Scholar
21. Nakaya, C. 1989 Waves on a viscous fluid down a vertical wall. Phys. Fluids A 1, 1143.CrossRefGoogle Scholar
22. Nguyen, L. T. & Balakotaiah, V. 2000 Modeling and experimental studies of wave evolution on free falling viscous films. Phys. Fluids 12, 2236–2256.CrossRefGoogle Scholar
23. Nusselt, W. 1916 Die oberflachenkondensation des wasserdampfes. Z. Verein. Deutsch. Ing. 50, 541–546.Google Scholar
24. Ochoa-Tapia, J. A. & Whitaker, S. 1995 Momentum transfer at the boundary between a porous medium and a homogeneous fluid i: theoretical development. Intl J. Heat Mass Transfer 38, 2635–2646.CrossRefGoogle Scholar
25. Ooshida, T. 1999 Surface equation of falling film flows with moderate Reynolds number and large but finite Weber number. Phys. Fluids 11, 3247–3269.Google Scholar
26. Oron, A., Davis, S. H. & Bankoff, S. G. 1997 Long scale evolution of thin films. Rev. Mod. Phys. 69, 931–980.CrossRefGoogle Scholar
27. Oron, A., Gottlieb, O. & Novbari, E. 2009 Weighted residual integral boundary-layer model of temporally excited falling liquid films. Eur. J. Mech. B/Fluids 28, 37–60.CrossRefGoogle Scholar
28. Pascal, J. P. 1999 Linear stability of fluid flow down a porous inclined plane. J. Phys. D: Appl. Phys. 32, 417–422.CrossRefGoogle Scholar
29. Popinet, S. 2003 Gerris: a tree-based adaptive solver for the incompressible euler equations in complex geometries. J. Comput. Phys. 190, 572–600.CrossRefGoogle Scholar
30. Popinet, S. 2009 An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 228, 5838–5866.CrossRefGoogle Scholar
31. Pumir, A., Manneville, P. & Pomeau, Y. 1983 On solitary waves running down an inclined plane. J. Fluid Mech. 135, 27–50.CrossRefGoogle Scholar
32. Ruyer-Quil, C. & Manneville, P. 2000 Improved modeling of flows down inclined planes. Eur. Phys. J. B 15, 357–369.CrossRefGoogle Scholar
33. Ruyer-Quil, C. & Manneville, P. 2002 Further accuracy and convergence results on the modeling of flows down inclined planes by weighted-residual approximations. Phys. Fluids 14, 170–183.CrossRefGoogle Scholar
34. Ruyer-Quil, C. & Manneville, P. 2005 On the speed of solitary waves running down a vertical wall. J. Fluid Mech. 531, 181–190.CrossRefGoogle Scholar
35. Ruyer-Quil, C., Trevelyan, P. M. J., Giorgiutti-Dauphiné, F., Duprat, C. & Kalliadasis, S. 2008 Modelling film flows down a fibre. J. Fluid Mech. 603, 431–462.CrossRefGoogle Scholar
36. Sadiq, M. & Usha, R. 2008 Thin Newtonian film flow down a porous inclined plane: stability analysis. Phys. Fluids 20, 022105.CrossRefGoogle Scholar
37. Salamon, T. R., Armstrong, R. C. & Brown, R. A. 1994 Travelling waves on vertical films: numerical analysis using the finite element method. Phys. Fluids 6, 2202–2220.CrossRefGoogle Scholar
38. Scheid, B., Kalliadasis, S., Ruyer-Quil, C. & Colinet, P. 2008 Interaction of three-dimensional hydrodynamic and thermocapillary instabilities in film flows. Phys. Rev. E 78, 066311.CrossRefGoogle ScholarPubMed
39. Scheid, B., Ruyer-Quil, C. & Manneville, P. 2006 Wave patterns in film flows: modelling and three-dimensional waves. J. Fluid Mech. 562, 183–222.CrossRefGoogle Scholar
40. Shkadov, V. Y. 1967 Wave flow regimes of a thin layer of viscous fluid subject to gravity (in Russian). Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza 1, 43. 51 (translation in 1970 Fluid Dyn. 2, 29–34) (Faraday, NY).Google Scholar
41. Shkadov, V. Ya. 1977 Solitary waves in a layer of viscous liquid. Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza 1, 63–66.Google Scholar
42. Shkadov, V. Ya. & Sisoev, G. M. 2004 Waves induced by instability in falling films of finite thickness. Fluid Dyn. Res. 35, 357–389.CrossRefGoogle Scholar
43. Smith, M. K. 1990 The mechanism for the long-wave instability in thin liquid films. J. Fluid Mech. 217, 469–485.CrossRefGoogle Scholar
44. Thiele, U., Goyeau, B. & Velarde, M. G. 2009 Stability analysis of thin film flow along a heated porous wall. Phys. Fluids 21, 014103.CrossRefGoogle Scholar
45. Trifonov, Y. Y. 2008a Stability of wavy downflow of films calculated by the Navier–Stokes equations. J. Appl. Mech. Tech. Phys. 49, 239–252.CrossRefGoogle Scholar
46. Trifonov, Y. Y. 2008b Wavy film flow down a vertical plate: comparisons between the results of integral approaches and full scale computations. J. Engng Thermophys. 17, 30–52.Google Scholar
47. Valdés-Parada, F. J., Alvarez-Ramirez, J., Goyeau, B. & Ochoa-Tapia, J. A. 2009 Computation of jump coefficients for momentum transfer between a porous medium and a fluid using a closed generalized transfer equation. Trans. Porous Med. 78, 439–457.Google Scholar
48. Valdés-Parada, F. J., Goyeau, B. & Ochoa-Tapia, J. A. 2007 Jump momentum boundary condition at a fluid-porous dividing surface: derivation of the closure problem. Chem. Engng Sci. 62, 4025–4039.CrossRefGoogle Scholar
49. Vinogradova, O. I. 1995 Drainage of a thin liquid film confined between hydrophobic surface. Langmuir 11, 2213–2220.CrossRefGoogle Scholar
50. Voronov, R. S. & Papavassiliou, D. V. 2008 Review of a fluid slip over superhydrophobic surfaces and its dependence on the contact angle. Ind. Engng Chem. Res. 47, 2455–2477.CrossRefGoogle Scholar
51. Whitaker, S. 1999 The Method of Volume Averaging. Kluwer.CrossRefGoogle Scholar
52. Whitham, G. B. 1974 Linear and Nonlinear Waves. Wiley-Interscience.Google Scholar
53. Yih, C. S. 1963 Stability of liquid flow down an inclined plane. Phys. Fluids 6, 321–334.CrossRefGoogle Scholar