Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Orlowski, Christopher T.
and
Girard, Anouck R.
2012.
Dynamics, stability, and control analyses of flapping wing micro-air vehicles.
Progress in Aerospace Sciences,
Vol. 51,
Issue. ,
p.
18.
Ol, Michael
and
Granlund, Kenneth
2012.
Abstraction of Aerodynamics of Flapping-Wings: Is it Quasi-Steady?.
Kang, Chang-Kwon
and
Shyy, Wei
2012.
Effects of Flexibility on the Aerodynamics of a Hovering Flexible Airfoil at Reynolds Number of 100 to 1000.
Kang, Chang-Kwon
and
Shyy, Wei
2012.
Passive Wing Rotation in Flexible Flapping Wing Aerodynamics.
Kang, Chang-kwon
and
Shyy, Wei
2013.
Scaling law and enhancement of lift generation of an insect-size hovering flexible wing.
Journal of The Royal Society Interface,
Vol. 10,
Issue. 85,
p.
20130361.
Aono, Hikaru
and
Liu, Hao
2013.
Flapping wing aerodynamics of a numerical biological flyer model in hovering flight.
Computers & Fluids,
Vol. 85,
Issue. ,
p.
85.
Yeo, Derrick
Atkins, Ella M.
Bernal, Luis P.
and
Shyy, Wei
2013.
Experimental Characterization of Lift on a Rigid Flapping Wing.
Journal of Aircraft,
Vol. 50,
Issue. 6,
p.
1806.
Mattheijssens, Joris
Marcel, Jean-Paul
Bosschaerts, Walter
and
Lefeber, Dirk
2013.
Performance of heaving and passively pitching hydrofoils.
Kang, Chang-Kwon
and
Shyy, Wei
2013.
Modeling of Instantaneous Passive Pitch of Flexible Flapping Wings.
Vandenheede, Ruben
Bernal, Luis
Gogulapati, Abhijit
Friedmann, Peretz
Kang, Chang-Kwon
Morrison, Christian
and
Shyy, Wei
2013.
Comparison of experiments on bio-inspired hover kinematics with the unsteady vortex model and CFD.
Deng, Hong-Bin
Xu, Yuan-Qing
Chen, Duan-Duan
Dai, Hu
Wu, Jian
and
Tian, Fang-Bao
2013.
On numerical modeling of animal swimming and flight.
Computational Mechanics,
Vol. 52,
Issue. 6,
p.
1221.
Hua, Ru-Nan
Zhu, Luoding
and
Lu, Xi-Yun
2013.
Locomotion of a flapping flexible plate.
Physics of Fluids,
Vol. 25,
Issue. 12,
Gogulapati, Abhijit
Friedmann, Peretz P.
Kheng, Eugene
and
Shyy, Wei
2013.
Approximate Aeroelastic Modeling of Flapping Wings in Hover.
AIAA Journal,
Vol. 51,
Issue. 3,
p.
567.
Kang, Chang-kwon
Aono, Hikaru
Sik Baik, Yeon
Bernal, Luis P.
and
Shyy, Wei
2013.
Fluid Dynamics of Pitching and Plunging Flat Plate at Intermediate Reynolds Numbers.
AIAA Journal,
Vol. 51,
Issue. 2,
p.
315.
Dawson, Jaderic
Smith, Todd
Parker, Gregory
Huang, George
and
Beran, Philip
2013.
Flapping Micro Air Vehicle: Wing Fabrication and Analysis.
Ha, Ngoc San
Truong, Quang Tri
Goo, Nam Seo
and
Park, Hoon Cheol
2013.
Relationship between wingbeat frequency and resonant frequency of the wing in insects.
Bioinspiration & Biomimetics,
Vol. 8,
Issue. 4,
p.
046008.
Dewey, Peter A.
Boschitsch, Birgitt M.
Moored, Keith W.
Stone, Howard A.
and
Smits, Alexander J.
2013.
Scaling laws for the thrust production of flexible pitching panels.
Journal of Fluid Mechanics,
Vol. 732,
Issue. ,
p.
29.
Moore, M. Nicholas J.
2014.
Analytical results on the role of flexibility in flapping propulsion.
Journal of Fluid Mechanics,
Vol. 757,
Issue. ,
p.
599.
Arora, Nipun
Jain, Anirudh
Singh, Apoorv
Gupta, Amit
Sanghi, Sanjeev
Aono, Hikaru
and
Shyy, Wei
2014.
Forward propulsion of a rigid plunging airfoil.
Kim, Ho-Young
Lee, Jun-Seong
Choi, Han-Lim
and
Han, Jae-Hung
2014.
Autonomous formation flight of multiple flapping-wing flying vehicles using motion capture system.
Aerospace Science and Technology,
Vol. 39,
Issue. ,
p.
596.
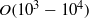 and the reduced frequency of
and the reduced frequency of 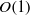 , the added mass force, related to the acceleration of the wing, is important. Based on the order of magnitude and energy balance arguments, a relationship between the propulsive force and the maximum relative wing-tip deformation parameter (
, the added mass force, related to the acceleration of the wing, is important. Based on the order of magnitude and energy balance arguments, a relationship between the propulsive force and the maximum relative wing-tip deformation parameter (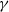 ) is established. The parameter depends on the density ratio, St, k, natural and flapping frequency ratio, and flapping amplitude. The lift generation, and the propulsive efficiency can be deduced by the same scaling procedures. It seems that the maximum propulsive force is obtained when flapping near the resonance, whereas the optimal propulsive efficiency is reached when flapping at about half of the natural frequency; both are supported by the reported studies. The established scaling relationships can offer direct guidance for micro air vehicle design and performance analysis.
) is established. The parameter depends on the density ratio, St, k, natural and flapping frequency ratio, and flapping amplitude. The lift generation, and the propulsive efficiency can be deduced by the same scaling procedures. It seems that the maximum propulsive force is obtained when flapping near the resonance, whereas the optimal propulsive efficiency is reached when flapping at about half of the natural frequency; both are supported by the reported studies. The established scaling relationships can offer direct guidance for micro air vehicle design and performance analysis.



