Article contents
Effect of the eigenvalues of the velocity gradient tensor on particle collisions
Published online by Cambridge University Press: 29 February 2016
Abstract
This study uses the eigenvalues of the local velocity gradient tensor to categorize the local flow structures in incompressible turbulent flows into different types of saddle nodes and vortices and investigates their effect on the local collision kernel of heavy particles. Direct numerical simulation (DNS) results show that most of the collisions occur in converging regions with real and negative eigenvalues. Those regions are associated not only with a stronger preferential clustering of particles, but also with a relatively higher collision kernel. To better understand the DNS results, a conceptual framework is developed to compute the collision kernel of individual flow structures. Converging regions, where two out of three eigenvalues are negative, posses a very high collision kernel, as long as a critical amount of rotation is not exceeded. Diverging regions, where two out of three eigenvalues are positive, have a very low collision kernel, which is governed by the third and negative eigenvalue. This model is not suited for particles with Stokes number 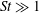 $St\gg 1$, where the contribution of particle collisions from caustics is dominant.
$St\gg 1$, where the contribution of particle collisions from caustics is dominant.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 6
- Cited by





