Hostname: page-component-77c89778f8-m8s7h Total loading time: 0 Render date: 2024-07-19T04:33:38.979Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of magnetic field on perturbation evolution in homogeneously sheared flows

Published online by Cambridge University Press:  12 November 2018

Divya Sri Praturi Open the ORCID record for Divya Sri Praturi [Opens in a new window] ,
Diane Collard  and
Sharath S. Girimaji
Divya Sri Praturi*
Affiliation:
Aerospace Engineering Department, Texas A&M University, College Station, TX 77843, USA
Diane Collard
Affiliation:
Department of Chemical Engineering, Kansas State University, Manhattan, KS 66506, USA
Sharath S. Girimaji
Affiliation:
Aerospace Engineering Department, Texas A&M University, College Station, TX 77843, USA Ocean Engineering Department, Texas A&M University, College Station, TX 77843, USA
*
†Email address for correspondence: divya249@tamu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The goal of this paper is to identify and characterize the fundamental mechanisms that contribute toward flow stabilization in sheared plasma flows. Toward that end, we investigate the evolution of velocity and magnetic field perturbations in homogeneously sheared magnetohydrodynamic (MHD) flows subjected to an imposed streamwise magnetic field. The influences of magnetic field strength (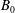$B_{0}$) and perturbation wavevector orientation (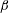$\unicode[STIX]{x1D6FD}$) are characterized using linear analysis and direct numerical simulations. The linear analysis of ideal MHD indicates that the perturbation evolution is governed by four processes: pressure redistribution, kinetic energy production, kinetic–magnetic energy exchange and magnetic energy production due to magnetic stretching. The interplay between these processes can be characterized by the ratio of shear-to-magnetic timescales (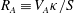$R_{A}\equiv V_{A}\unicode[STIX]{x1D705}/S$) and 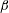$\unicode[STIX]{x1D6FD}$, where 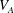$V_{A}$, $\unicode[STIX]{x1D705}$ and 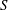$S$ are Alfvén wave speed, initial wavenumber and mean flow shear, respectively. For cases with low values of 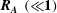$\boldsymbol{R}_{\boldsymbol{A}}~(\ll \mathbf{1})$, a three-stage perturbation evolution is seen. At the first stage, pressure redistribution and production dominate leading to hydrodynamic-type behaviour. In the second stage, the onset of magnetic stretching process leads to an increase in magnetic energy. At late stages, production subsides and the dynamics is dominated by harmonic exchange between velocity and magnetic fields. For cases of 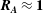$\boldsymbol{R}_{\boldsymbol{A}}\approx \mathbf{1}$, the magnetic field reacts rapidly enough that hydrodynamic and magnetic production stages occur simultaneously followed by harmonic exchange. In the case of 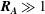$\boldsymbol{R}_{\boldsymbol{A}}\gg 1$, all three stages occur simultaneously leading to harmonic exchange between kinetic and magnetic energies without any perturbation growth. For all cases considered, the late stage harmonic exchange results in equipartition between perturbation magnetic and kinetic energies. For a given 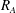$R_{A}$, the effect of increasing 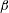$\unicode[STIX]{x1D6FD}$ is to reduce the intensity of coupling and progressively slow down the three stages of evolution. For spanwise wavevector perturbations, the velocity–magnetic field interaction mechanism vanishes and there is no effect of pressure or magnetic field on individual velocity components.

JFM classification

MHD and Electrohydrodynamics: MHD turbulence Wakes/Jets: Shear layers Wakes/Jets: Wakes/Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 858 , 10 January 2019 , pp. 852 - 880
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Araya, D. B., Ebersohn, F. H., Anderson, S. E. & Girimaji, S. S. 2015 Magneto-gas kinetic method for nonideal magnetohydrodynamic flows: verification protocol and plasma jet simulations. J. Fluids Engng 137 (8), 081302.Google Scholar
Baron, F.1982 Macro-simulation tridimensionnelle d’écoulements turbulents cisailles. PhD thesis, Université Pierre et Marie Curie, Paris.Google Scholar
Batchelor, G. K. & Proudman, I. 1954 The effect of rapid distortion of a fluid in turbulent motion. Q. J. Mech. Appl. Maths 7 (1), 83–103.Google Scholar
Belle-Hamer, A. L. La, Otto, A. & Lee, L. C. 1994 Magnetic reconnection in the presence of sheared plasma flow: intermediate shock formation. Phys. Plasmas 1 (3), 706–713.Google Scholar
Cambon, C., Coleman, G. N. & Mansour, N. N. 1993 Rapid distortion analysis and direct simulation of compressible homogeneous turbulence at finite Mach number. J. Fluid Mech. 257, 641–665.Google Scholar
Chagelishvili, G. D., Hristov, T. S., Chanishvili, R. G. & Lominadze, J. G. 1993 Mechanism of energy transformations in shear magnetohydrodynamic flows. Phys. Rev. E 47 (1), 366–374.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydrodynamic Stability. Oxford University Press.Google Scholar
Chatterjee, D., Chatterjee, K. & Mondal, B. 2012 Control of flow separation around bluff obstacles by transverse magnetic field. J. Fluids Engng 134 (9), 091102.Google Scholar
Diaz, F. R. C. 2000 The VASIMR rocket. Sci. Am. 283 (5), 90–97.Google Scholar
Dimitrov, Z. D., Maneva, Y. G., Hristov, T. S. & Mishonov, T. M. 2011 Over-reflection of slow magnetosonic waves by homogeneous shear flow: analytical solution. Phys. Plasmas 18 (8), 082110.Google Scholar
Faganello, M., Califano, F. & Pegoraro, F. 2008 Time window for magnetic reconnection in plasma configurations with velocity shear. Phys. Rev. Lett. 101 (17), 175003.Google Scholar
Goossens, M. 2012 An Introduction to Plasma Astrophysics and Magnetohydrodynamics, vol. 294. Springer Science & Business Media.Google Scholar
Herault, J., Rincon, F., Cossu, C., Lesur, G., Ogilvie, G. I. & Longaretti, P. Y. 2011 Periodic magnetorotational dynamo action as a prototype of nonlinear magnetic-field generation in shear flows. Phys. Rev. E 84 (3), 036321.Google Scholar
Karimi, M. & Girimaji, S. S. 2016 Suppression mechanism of Kelvin–Helmholtz instability in compressible fluid flows. Phys. Rev. E 93 (4), 041102.Google Scholar
Karimi, M. & Girimaji, S. S. 2017 Influence of orientation on small perturbation evolution in compressible shear layers with the inflection point. Phys. Rev. E 95 (3), 033112.Google Scholar
Kirillov, O. N., Stefani, F. & Fukumoto, Y. 2014 Local instabilities in magnetized rotational flows: a short-wavelength approach. J. Fluid Mech. 760, 591–633.Google Scholar
Kumar, G., Bertsch, R. L. & Girimaji, S. S. 2014 Stabilizing action of pressure in homogeneous compressible shear flows: effect of Mach number and perturbation obliqueness. J. Fluid Mech. 760, 540–566.Google Scholar
Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98 (2), 243–251.Google Scholar
Lau, Y. Y. & Liu, C. S. 1980 Stability of shear flow in a magnetized plasma. Phys. Fluids 23 (5), 939–941.Google Scholar
Lerner, J. & Knobloch, E. 1985 The stability of dissipative magnetohydrodynamic shear flow in a parallel magnetic field. Geophys. Astrophys. Fluid Dyn. 33 (1–4), 295–314.Google Scholar
Li, L.-X. 2002 Jet collimation by small-scale magnetic fields. Astrophys. J. 564 (1), 108–112.Google Scholar
Livio, M. 1999 Astrophysical jets: a phenomenological examination of acceleration and collimation. Phys. Rep. 311 (3), 225–245.Google Scholar
McWilliams, J. C. 2012 The elemental shear dynamo. J. Fluid Mech. 699, 414–452.Google Scholar
Mikellides, P. G., Turchi, P. J. & Roderick, N. F. 2000 Applied-field magnetoplasmadynamic thrusters. Part 1. Numerical simulations using the MACH2 code. J. Propul. Power 16 (5), 887–893.Google Scholar
Miura, A. & Pritchett, P. L. 1982 Nonlocal stability analysis of the MHD Kelvin–Helmholtz instability in a compressible plasma. J. Geophys. Res. 87 (A9), 7431–7444.Google Scholar
Olsen, C. S., Ballenger, M. G., Carter, M. D., Díaz, F. R. C., Giambusso, M., Glover, T. W., Ilin, A. V., Squire, J. P., Longmier, B. W., Bering, E. A. III & Cloutier, P. A. 2013 An experimental study of plasma detachment from a magnetic nozzle in the plume of the VASIMR® engine. In Proceedings of the 33rd International Electric Propulsion Conference, Electric Rocket Propulsion Society.Google Scholar
Pope, S. B. 2001 Turbulent Flows. IOP Publishing.Google Scholar
Rogallo, R. S.1981 Numerical experiments in homogeneous turbulence. NASA Technical Memorandum 81315.Google Scholar
Samtaney, R. 2003 Suppression of the Richtmyer–Meshkov instability in the presence of a magnetic field. Phys. Fluids 15 (8), L53–L56.Google Scholar
Sarkar, S., Erlebacher, G., Hussaini, M. Y. & Kreiss, H. O. 1991 The analysis and modelling of dilatational terms in compressible turbulence. J. Fluid Mech. 227, 473–493.Google Scholar
Simone, A., Coleman, G. & Cambon, C. 1997 The effect of compressibility on turbulent shear flow: a rapid distortion-theory and direct numerical-simulation study. J. Fluid Mech. 330, 307–338.Google Scholar
Taylor, G. I. & Batchelor, G. K. 1949 The effect of wire gauze on small disturbances in a uniform stream. Q. J. Mech. Appl. Maths 2 (1), 1–29.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261 (5121), 578–584.Google Scholar
Xie, Z. & Girimaji, S. S. 2014 Instability of Poiseuille flow at extreme Mach numbers: linear analysis and simulations. Phys. Rev. E 89 (4), 043001.Google Scholar
Zaqarashvili, T. V. 1997 On a possible generation mechanism of a solar cycle. Astrophys. J. 487 (2), 930–935.Google Scholar