Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-16T18:16:57.979Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of enclosure height on the structure and stability of shear layers induced by differential rotation

Published online by Cambridge University Press:  15 January 2015

Tony Vo ,
Luca Montabone  and
Gregory J. Sheard
Tony Vo
Affiliation:
The Sheard Lab, Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
Luca Montabone
Affiliation:
Atmospheric, Oceanic and Planetary Physics, University of Oxford, Parks Road, Oxford OX1 3PU, UK
Gregory J. Sheard*
Affiliation:
The Sheard Lab, Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
*
†Email address for correspondence: Greg.Sheard@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The structure and stability of Stewartson shear layers with different heights are investigated numerically via axisymmetric simulation and linear stability analysis, and a validation of the quasi-two-dimensional model is performed. The shear layers are generated in a rotating cylindrical tank with circular disks located at the lid and base imposing a differential rotation. The axisymmetric model captures both the thick and thin nested Stewartson layers, which are scaled by the Ekman number (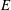$\mathit{E}\,$) as 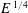$\mathit{E}\,^{1/4}$ and 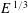$\mathit{E}\,^{1/3}$ respectively. In contrast, the quasi-two-dimensional model only captures the 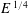$\mathit{E}\,^{1/4}$ layer as the axial velocity required to invoke the 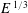$\mathit{E}\,^{1/3}$ layer is excluded. A direct comparison between the axisymmetric base flows and their linear stability in these two models is examined here for the first time. The base flows of the two models exhibit similar flow features at low Rossby numbers (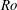$\mathit{Ro}$), with differences evident at larger 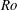$\mathit{Ro}$ where depth-dependent features are revealed by the axisymmetric model. Despite this, the quasi-two-dimensional model demonstrates excellent agreement with the axisymmetric model in terms of the shear-layer thickness and predicted stability. A study of various aspect ratios reveals that a Reynolds number based on the theoretical Ekman layer thickness is able to describe the transition of a base flow that is reflectively symmetric about the mid-plane to a symmetry-broken state. Additionally, the shear-layer thicknesses scale closely to the expected 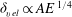${\it\delta}_{vel}\propto A\mathit{E}\,^{1/4}$ and 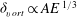${\it\delta}_{vort}\propto A\mathit{E}\,^{1/3}$ for shear layers that are not affected by the confinement ($A\mathit{E}\,^{1/4}\lesssim 0.34$ in this system, the ratio of tank height to shear-layer radius). The linear stability analysis reveals that the ratio of Stewartson layer radius to thickness should be greater than 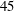$45$ for the stability of the flow to be independent of aspect ratio. Thus, for sufficiently small 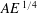$A\mathit{E}\,^{1/4}$ and 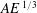$A\mathit{E}\,^{1/3}$, the flow characteristics remain similar and the linear stability of the flow can be described universally when the azimuthal wavelength is scaled against 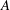$A$. The analysis also recovers an asymptotic scaling for the normalized azimuthal wavelength which suggests that 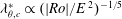${\it\lambda}_{{\it\theta},c}^{\ast }\propto (|\mathit{Ro}|/\mathit{E}\,^{2})^{-1/5}$ for geometry-independent shear layers at marginal stability.

JFM classification

Instability: Instability Geophysical and Geological Flows: Rotating flows Wakes/Jets: Shear layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 765 , 25 February 2015 , pp. 45 - 81
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Space Science Institute, Boulder, CO 80301, USA.

References

Aguiar, A. C. B.2008 Instabilities of a shear layer in a barotropic rotating fluid, PhD Thesis, University of Oxford.Google Scholar
Aguiar, A. C. B., Read, P. L., Wordsworth, R. D., Salter, T. & Hiro Yamazaki, Y. 2010 A laboratory model of Saturn’s north polar hexagon. Icarus 206 (2), 755–763.CrossRefGoogle Scholar
Avila, M. 2012 Stability and angular-momentum transport of fluid flows between corotating cylinders. Phys. Rev. Lett. 108 (12), 124501.CrossRefGoogle ScholarPubMed
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Bergeron, K., Coutsias, E. A., Lynov, J. P. & Nielsen, A. H. 2000 Dynamical properties of forced shear layers in an annular geometry. J. Fluid Mech. 402 (1), 255–289.CrossRefGoogle Scholar
Blackburn, H. M. & Sherwin, S. J. 2004 Formulation of a Galerkin spectral element – Fourier method for three-dimensional incompressible flows in cylindrical geometries. J. Comput. Phys. 197 (2), 759–778.CrossRefGoogle Scholar
Busse, F. H. 1968 Shear flow instabilities in rotating systems. J. Fluid Mech. 33 (3), 577–589.CrossRefGoogle Scholar
Chomaz, J. M., Rabaud, M., Basdevant, C. & Couder, Y. 1988 Experimental and numerical investigation of a forced circular shear layer. J. Fluid Mech. 187, 115–140.Google Scholar
Cogan, S. J., Ryan, K. & Sheard, G. J. 2011 Symmetry breaking and instability mechanisms in medium depth torsionally driven open cylinder flows. J. Fluid Mech. 672, 521–544.CrossRefGoogle Scholar
Drazin, P. G. & Howard, L. N. 1966 Hydrodynamic Stability of Parallel Flow of Inviscid Fluid Vol. 9. Academic.CrossRefGoogle Scholar
Fletcher, L. N., Irwin, P. G. J., Orton, G. S., Teanby, N. A., Achterberg, R. K., Bjoraker, G. L., Read, P. L., Simon-Miller, A. A., Howett, C., de Kok, R., Bowles, N., Calcutt, S. B., Hesman, B. & Flasar, F. M. 2008 Temperature and composition of Saturn’s polar hotspots and hexagon. Science 319 (5859), 79–81.CrossRefGoogle Scholar
Früh, W. G. & Nielsen, A. H. 2003 On the origin of time-dependent behaviour in a barotropically unstable shear layer. Nonlinear Process. Geophys. 10 (3), 289–302.CrossRefGoogle Scholar
Früh, W. G. & Read, P. L. 1999 Experiments on a barotropic rotating shear layer. Part 1. Instability and steady vortices. J. Fluid Mech. 383, 143–173.Google Scholar
Gissinger, C., Goodman, J. & Ji, H. 2012 The role of boundaries in the magnetorotational instability. Phys. Fluids 24 (7), 074109.CrossRefGoogle Scholar
Godfrey, D. A. 1988 A hexagonal feature around Saturn’s north pole. Icarus 76, 335–356.Google Scholar
Godfrey, D. A. & Moore, V. 1986 The Saturnian ribbon feature – a baroclinically unstable model. Icarus 68 (2), 313–343.CrossRefGoogle Scholar
Gombosi, T. I. & Ingersoll, A. P. 2010 Saturn: atmosphere, ionosphere, and magnetosphere. Science 327 (5972), 1476–1479.CrossRefGoogle ScholarPubMed
Hollerbach, R. & Fournier, A. 2004 End-effects in rapidly rotating cylindrical Taylor–Couette flow. In MHD Couette Flows: Experiments and Models (ed. Rosner, R., Rüdiger, G. & Bonanno, A.), AIP Conference Proceedings, vol. 733, pp. 114–121.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97, 414–443.CrossRefGoogle Scholar
van de Konijnenberg, J. A., Nielsen, A. H., Juul Rasmussen, J. & Stenum, B. 1999 Shear-flow instability in a rotating fluid. J. Fluid Mech. 387, 177–204.CrossRefGoogle Scholar
Kuo, H. 1949 Dynamic instability of two-dimensional nondivergent flow in a barotropic atmosphere. J. Atmos. Sci. 6, 105–122.Google Scholar
Lian, Y. & Showman, A. P. 2008 Deep jets on gas-giant planets. Icarus 194 (2), 597–615.Google Scholar
Liu, W. 2008 Magnetized Ekman layer and Stewartson layer in a magnetized Taylor–Couette flow. Phys. Rev. E 77 (5), 056314.Google Scholar
Luz, D., Berry, D. L., Piccioni, G., Drossart, P., Politi, R., Wilson, C. F., Erard, S. & Nuccilli, F. 2011 Venus’s southern polar vortex reveals precessing circulation. Science 332 (6029), 577–580.Google Scholar
Montabone, L., Wordsworth, R., Aguiar, A. C. B., Jacoby, T., Manfrin, M., Read, P. L., Castrejon-Pita, A., Gostiaux, L., Sommeria, J., Viboud, S. & Didelle, H. 2010 Barotropic instability of planetary polar vortices: CIV analysis of specific multi-lobed structures. In Proceedings of the HYDRALAB III Joint Transnational Access User Meeting, Hannover, p. 191.Google Scholar
Niino, H. & Misawa, N. 1984 An experimental and theoretical study of barotropic instability. J. Atmos. Sci. 41 (12), 1992–2011.Google Scholar
Paoletti, M. S., van Gils, D. P. M., Dubrulle, B., Sun, C., Lohse, D. & Lathrop, D. P. 2012 Angular momentum transport and turbulence in laboratory models of Keplerian flows. Astronom. Astrophys. 547, A64.Google Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics. Springer.Google Scholar
Piccioni, G., Drossart, P., Sanchez-Lavega, A., Hueso, R., Taylor, F. W., Wilson, C. F., Grassi, D., Zasova, L., Moriconi, M. & Adriani, A. et al. 2007 South-polar features on Venus similar to those near the north pole. Nature 450 (7170), 637–640.CrossRefGoogle ScholarPubMed
Rabaud, M. & Couder, Y. 1983 Shear-flow instability in a circular geometry. J. Fluid Mech. 136, 291–319.CrossRefGoogle Scholar
Rayleigh, L. 1880 On the stability, or instability, of certain fluid motions. Proc. Lond. Math. Soc. 11, 57–72.Google Scholar
Read, P. L. 1988 On the scale of baroclinic instability in deep, compressible atmospheres. Q. J. R. Meteorol. Soc. 114 (480), 421–437.Google Scholar
Sánchez-Lavega, A., Río-Gaztelurrutia, T., Hueso, R., Pérez-Hoyos, S., García-Melendo, E., Antuñano, A., Mendikoa, I., Rojas, J. F., Lillo, J. & Barrado-Navascués, D. et al. 2014 The long-term steady motion of Saturn’s hexagon and the stability of its enclosed jet stream under seasonal changes. Geophys. Res. Lett. 41 (5), 1425–1431.CrossRefGoogle Scholar
Schaeffer, N. & Cardin, P. 2005 Quasigeostrophic model of the instabilities of the Stewartson layer in flat and depth-varying containers. Phys. Fluids 17, 104111.CrossRefGoogle Scholar
Schartman, E., Ji, H., Burin, M. J. & Goodman, J. 2012 Stability of quasi-Keplerian shear flow in a laboratory experiment. Astronom. Astrophys. 543 (A94).CrossRefGoogle Scholar
Sheard, G. J. 2009 Flow dynamics and wall shear-stress variation in a fusiform aneurysm. J. Engng Math. 64 (4), 379–390.CrossRefGoogle Scholar
Sheard, G. J. 2011 Wake stability features behind a square cylinder: focus on small incidence angles. J. Fluids Struct. 27, 734–742.Google Scholar
Sheard, G. J. & Ryan, K. 2007 Pressure-driven flow past spheres moving in a circular tube. J. Fluid Mech. 592, 233–262.Google Scholar
Smith, S. H. 1984 The development of nonlinearities in the $E^{1/3}$ Stewartson layer. Q. J. Mech. Appl. Maths 37 (1), 75–85.CrossRefGoogle Scholar
Sommeria, J., Meyers, S. D. & Swinney, H. L. 1991 Experiments on vortices and Rossby waves in eastward and westward jets. Nonlinear Topics Ocean Phys. 109, 227–269.Google Scholar
Stewartson, K. 1957 On almost rigid rotations. J. Fluid Mech. 3, 17–26.CrossRefGoogle Scholar
Szklarski, J. & Rüdiger, G. 2007 Ekman–Hartmann layer in a magnetohydrodynamic Taylor–Couette flow. Phys. Rev. E 76 (6), 066308.Google Scholar
Taylor, F. W., Beer, R., Chahine, M. T., Diner, D. J., Elson, L. S., Haskins, R. D., McCleese, D. J., Martonchik, J. V., Reichley, P. E. & Bradley, S. P. 1980 Structure and meteorology of the middle atmosphere of Venus: infrared remote sensing from the Pioneer Orbiter. J. Geophys. Res. 85 (A13), 7963–8006.CrossRefGoogle Scholar
Vo, T., Montabone, L. & Sheard, G. J. 2014 Linear stability analysis of a shear layer induced by differential coaxial rotation within a cylindrical enclosure. J. Fluid Mech. 738, 299–334.CrossRefGoogle Scholar
Vooren, A. I. 1992 The Stewartson layer of a rotating disk of finite radius. J. Engng Maths 26 (1), 131–152.Google Scholar
Williams, G. P. 2003 Jovian dynamics. Part III: Multiple, migrating, and equatorial jets. J. Atmos. Sci. 60 (10), 1270–1296.2.0.CO;2>CrossRefGoogle Scholar