Hostname: page-component-77c89778f8-vsgnj Total loading time: 0 Render date: 2024-07-17T17:08:05.290Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of detonations with a constant mean flow divergence

Published online by Cambridge University Press:  25 April 2018

Matei I. Radulescu Open the ORCID record for Matei I. Radulescu [Opens in a new window]  and
Bijan Borzou
Matei I. Radulescu*
Affiliation:
Department of Mechanical Engineering, University of Ottawa, ON K1N 6N5, Canada
Bijan Borzou
Affiliation:
Department of Mechanical Engineering, University of Ottawa, ON K1N 6N5, Canada
*
†Email address for correspondence: matei@uottawa.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

An exponential horn geometry is introduced in order to establish cellular detonations with a constant mean lateral mass divergence, propagating at quasi-steady speeds below the Chapman–Jouguet value. The experiments were conducted in 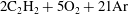$2\text{C}_{2}\text{H}_{2}+5\text{O}_{2}+21\text{Ar}$ and 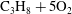$\text{C}_{3}\text{H}_{8}+5\text{O}_{2}$. Numerical simulations were also performed for weakly unstable cellular detonations to test the validity of the exponential horn geometry. The experiments and simulations demonstrated that such quasi-steady state detonations can be realized, hence permitting us to obtain the relations between the detonation speed and mean lateral flow divergence for cellular detonations in an unambiguous manner. The experimentally obtained speed ($D$) dependencies on divergence (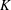$K$) were compared with the predictions for steady detonations with lateral flow divergence obtained with the real thermo-chemical data of the mixtures. For the 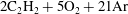$2\text{C}_{2}\text{H}_{2}+5\text{O}_{2}+21\text{Ar}$ system, reasonable agreement was found between the experiments and steady wave prediction, particularly for the critical divergence leading to failure. Observations of the reaction zone structure in these detonations indicated that all the gas reacted very close to the front, as the transverse waves were reactive. The experiments obtained in the much more unstable detonations in 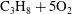$\text{C}_{3}\text{H}_{8}+5\text{O}_{2}$ showed significant differences between the experimentally derived 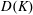$D(K)$ curve and the prediction of steady wave propagation. The latter was found to significantly under-predict the detonability of cellular detonations. The transverse waves in this mixture were found to be non-reactive, hence permitting the shedding of non-reacted pockets, which burn via turbulent flames on their surface. It is believed that the large differences between experiment and the inviscid model in this class of cellular structures is due to the importance of diffusive processes in the burn-out of the non-reacted pockets. The empirical tuning of a global one-step chemical model to describe the macro-scale kinetics in cellular detonations revealed that the effective activation energy was lower by 14 % in 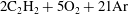$2\text{C}_{2}\text{H}_{2}+5\text{O}_{2}+21\text{Ar}$ and 54 % in the more unstable 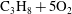$\text{C}_{3}\text{H}_{8}+5\text{O}_{2}$ system. This confirms previous observations that diffusive processes in highly unstable detonations are responsible for reducing the thermal ignition character of the gases processed by the detonation front.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Detonation waves Reacting Flows: Reacting Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 845 , 25 June 2018 , pp. 346 - 377
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Austin, J.2003 The role of instability in gaseous detonation. PhD thesis, California Institute of Technology, Pasadena, California.Google Scholar
Bdzil, J. B. & Stewart, D. S. 2007 The dynamics of detonation in explosive systems. Annu. Rev. Fluid Mech. 39, 263–292.Google Scholar
Bhattacharjee, R.2013 Experimental investigation of detonation re-initiation mechanisms following a Mach reflection of a quenched detonation. MSc thesis, Department of Mechanical Engineering, University of Ottawa, Ottawa, ON.CrossRefGoogle Scholar
Blanquart, G.2018 CaltechMech. California institute of technology (http://www.theforce.caltech.edu/caltechmech/index.html).Google Scholar
Borzou, B.2016 The influence of cellular structure on the dynamics of detonations with constant mass divergence. PhD thesis, University of Ottawa, Ottawa, ON.Google Scholar
Camargo, A., Ng, H. D., Chao, J. & Lee, J. H. S. 2010 Propagation of near-limit gaseous detonations in small diameter tubes. Shock Waves 20, 499–508.CrossRefGoogle Scholar
Chao, J., Ng, H. D. & Lee, J. H. S. 2009 Detonability limits in thin annular channels. Proc. Combust. Inst. 32, 2349–2354.Google Scholar
Chinnayya, A., Hadjadj, A. & Ngomo, D. 2013 Computational study of detonation wave propagation in narrow channels. Phys. Fluids 25, 036101.Google Scholar
Dennis, K., Maley, L., Liang, Z. & Radulescu, M. I. 2014 Implementation of large scale shadowgraphy in hydrogen explosion phenomena. Intl J. Hydrog. Energy 39 (21), 11346–11353.Google Scholar
Dupré, G., Péraldi, O., Joannon, J., Lee, J. H. S. & Knystautas, R. 1991 Limit criterion of detonation in circular tubes. In Dynamics of Detonations and Explosions: Detonations (ed. Kuhl, A. et al. ), Progress in Astronautics and Aeronautics, vol. 133, pp. 156–169. American Institute of Aeronautics and Astronautics.Google Scholar
Falle, S. A. E. G. & Giddings, J. R. 1993 Body capturing using adaptive Cartesian grids. In Numerical Methods for Fluid Dynamics IV, pp. 337–343. Oxford University Press.Google Scholar
Falle, S. A. E. G. 1991 Self-similar jets. Mon. Not. R. Astron. Soc. 250, 581–596.CrossRefGoogle Scholar
Fay, J. A. 1959 Two-dimensional gaseous detonations:velocity deficit. Phys. Fluids 2, 283–289.Google Scholar
Fickett, W. & Davis, W. C. 1979 Detonation Theory and Experiment. Dover.Google Scholar
Gamezo, V. N., Desbordes, D. & Oran, E. S. 1999 Formation and evolution of two-dimenional cellular detonations. Combust. Flame 116, 154–165.CrossRefGoogle Scholar
Gamezo, V. N., Vasil’ev, A. A., Khokhlov, A. M. & Oran, E. S. 2000 Fine cellular structures produced by marginal detonations. Proc. Combust. Inst. 28, 611–617.Google Scholar
Gao, Y., Zhang, B., Ng, H. D. & Lee, J. H. S. 2016 An experimental investigation of detonation limits in hydrogen–oxygen–argon mixtures. Intl J. Hydrog. Energy 41 (14), 6076–6083.CrossRefGoogle Scholar
Goodwin, D. G., Moffat, H. K. & Speth, R. L.2017 Cantera: an object-oriented software toolkit for chemical kinetics, thermodynamics, and transport processes. http://www.cantera.org, version 2.3.0.Google Scholar
Han, W. H., Huang, J., Du, N., Liu, Z. G., Kong, W. J. & Wang, C. 2017a Effect of cellular instability on the initiation of cylindrical detonations. Chin. Phys. Lett. 34 (5), 054701.Google Scholar
Han, W. H., Kong, W. J., Gao, Y. & Law, C. K. 2017b The role of global curvature on the structure and propagation of weakly unstable cylindrical detonations. J. Fluid Mech. 813 (5), 458–481.Google Scholar
He, L. T. & Clavin, P. 1994 On the direct initiation of gaseous detonations by an energy source. J. Fluid Mech. 277, 227–284.Google Scholar
Kao, S.2008 Detonation stability with reversible kinetics. PhD thesis, California Institute of Technology, Pasadena, California.Google Scholar
Kao, S. & Shepherd, J. E.2008 Numerical solution methods for control volume explosions and ZND detonation structure. GALCIT Rep. FM2006.007. California Institute of Technology, Pasadena, California.Google Scholar
Kasimov, A. R. & Stewart, D. S. 2005 Asymptotic theory of evolution and failure of self-sustained detonations. J. Fluid Mech. 525, 161–192.Google Scholar
Klein, R., Krok, J. C. & Shepherd, J. E.1995 Curved quasi-steady detonations: asymptotic analysis and detailed chemical kinetics. GALCIT Rep. FM 95-04. California Institute of Technology, Pasadena, California.Google Scholar
Lee, J. H. S. 2008 The Detonation Phenomenon. Cambridge University Press.Google Scholar
Maxwell, B., Bhattacharjee, R., Lau-Chapdelaine, S., Falle, S., Sharpe, G. J. & Radulescu, M. I. 2017 Influence of turbulent fluctuations on detonation propagation. J. Fluid Mech. 818, 646–696.Google Scholar
Mazaheri, K., Mahmoudi, Y., Sabzpooshani, M. & Radulescu, M. I. 2015 Experimental and numerical investigation of propagation mechanism of gaseous detonations in channels with porous walls. Combust. Flame 162, 2638–2659.Google Scholar
McBride, B. J. & Gordon, S.1996 Computer program for calculation of complex chemical equilibrium compositions. Tech. Rep. E-8017-1, National Aeronautics and Space Administration report, Washington DC.Google Scholar
Moen, I. O., Donato, M., Knystautas, R. & Lee, J. H. S. 1981 The influence of confinement on the propagation of detonations near the detonability limits. Proc. Combust. Inst. 18, 1615–1622.Google Scholar
Radulescu, M. I.2003 The propagation and failure mechanisms of gaseous detonations: experiments in porous-walled tubes. PhD thesis, Department of Mechanical Engineering, McGill University, Montreal, QC.Google Scholar
Radulescu, M. I. 2017 The usefulness of a 1D hydrodynamic model for the detonation structure for predicting detonation dynamic parameters. Extended abstract 1140. In Proceedings of the 26th International Colloquium on the Dynamics of Explosions and Reactive Systems, Boston, MA. Institute for Dynamics of Explosions and Reactive Systems.Google Scholar
Radulescu, M. I. & Lee, J. H. S. 2002 The failure mechanism of gaseous detonations: experiments in porous wall tubes. Combust. Flame 131, 29–46.CrossRefGoogle Scholar
Radulescu, M. I., Sharpe, G. J. & Law, C. K. 2007a Effect of cellular instabilities on the blast initiation of weakly unstable detonations. In Proceedings of the 21st International Colloquium on the Dynamics of Explosions and Reactive Systems, Poitiers, France. Institute for Dynamics of Explosions and Reactive Systems.Google Scholar
Radulescu, M. I., Sharpe, G. J., Law, C. K. & Lee, J. H. S. 2007b The hydrodynamic structure of unstable cellular detonations. J. Fluid Mech. 580, 31–81.Google Scholar
Reynaud, M., Virot, F. & Chinnayya, A. 2017 A computational study of the interaction of gaseous detonations with a compressible layer. Phys. Fluids 29 (5), 056101.Google Scholar
Richtmyer, R. D. & Morton, K. W. 1967 Difference Methods for Initial-Value Problems. Interscience Publishers.Google Scholar
Romick, C. M., Aslam, T. D. & Powers, J. M. 2012 The effect of diffusion on the dynamics of unsteady detonations. J. Fluid Mech. 699, 453–464.Google Scholar
Sharpe, G. J. & Quirk, J. J. 2008 Nonlinear cellular dynamics of the idealized detonation model: regular cells. Combust. Theor. Model. 12 (1), 1–21.Google Scholar
Shepherd, J. E. 2009 Detonation in gases. Proc. Combust. Inst. 32, 83–98.Google Scholar
Short, M. & Bdzil, J. B. 2003 Propagation laws for steady curved detonations with chain-branching kinetics. J. Fluid Mech. 479, 39–64.Google Scholar
Subbotin, V. A. 1976 Two kinds of transverse wave structures in multifront detonation. Combust. Explos. Shock Waves 11, 83–88.Google Scholar
Van Leer, B. 1977 Towards the ultimate conservative difference scheme. Part III. Upstream-centered finite-difference schemes for ideal compressible flow. J. Comput. Phys. 23, 263–275.Google Scholar
Wang, H., You, X., Joshi, A. V., Davis, S. G., Laskin, A., Egolfopoulos, F. & Law, C. K.2007 USC Mech version II: high-temperature combustion reation model of H2/CO/C1-C4 compounds (http://ignis.usc.edu/Mechanisms/USC-Mech-II.htm).Google Scholar
Whitham, G. B. 1974 Linear and Nonlinear Waves. Wiley.Google Scholar
Williams, F. A. 1985 Combustion Theory, 2nd edn. Benjamin/Cummings.Google Scholar
Williams, F. A.2014 Chemical-Kinetic Mechanisms for Combustion Applications. San Diego Mechanism web page, Mechanical and Aerospace Engineering (Combustion Research), University of California at San Diego (http://combustion.ucsd.edu).Google Scholar
Wood, W. W. & Kirkwood, J. G. 1954 Diameter effect in condensed explosives: the relation between velocity and radius of curvature of the detonation wave. J. Chem. Phys. 22 (11), 1920–1924.Google Scholar
Wood, W. W. & Kirkwood, J. G. 1957 Hydrodynamics of a reacting and relaxing fluid. J. Appl. Phys. 28, 395–398.Google Scholar
Yao, J. & Stewart, D. S. 1995 On the normal detonation shock velocity–curvature relationship for materials with large activation energy. Combust. Flame 100, 519–528.Google Scholar