Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-26T02:37:34.849Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of a high-Reynolds-number bubble rising within a thin gap

Published online by Cambridge University Press:  06 August 2012

Véronique Roig ,
Matthieu Roudet ,
Frédéric Risso  and
Anne-Marie Billet
Véronique Roig*
Affiliation:
Institut de Mécanique des Fluides de Toulouse, Université de Toulouse (INPT, UPS) and CNRS. Allée C. Soula, Toulouse, 31400, France Fédération de recherche FERMaT, CNRS, allée C. Soula, Toulouse, 31400, France
Matthieu Roudet
Affiliation:
Institut de Mécanique des Fluides de Toulouse, Université de Toulouse (INPT, UPS) and CNRS. Allée C. Soula, Toulouse, 31400, France Laboratoire de Génie Chimique, Université de Toulouse (INPT,UPS) and CNRS. 4 allée E. Monso, BP74233, Toulouse CEDEX 4, 31432, France Fédération de recherche FERMaT, CNRS, allée C. Soula, Toulouse, 31400, France
Frédéric Risso
Affiliation:
Institut de Mécanique des Fluides de Toulouse, Université de Toulouse (INPT, UPS) and CNRS. Allée C. Soula, Toulouse, 31400, France Fédération de recherche FERMaT, CNRS, allée C. Soula, Toulouse, 31400, France
Anne-Marie Billet
Affiliation:
Laboratoire de Génie Chimique, Université de Toulouse (INPT,UPS) and CNRS. 4 allée E. Monso, BP74233, Toulouse CEDEX 4, 31432, France Fédération de recherche FERMaT, CNRS, allée C. Soula, Toulouse, 31400, France
*
†Email address for correspondence: roig@imft.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We report an experimental analysis of path and shape oscillations of an air bubble of diameter 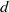rising in water at high Reynolds number 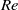in a vertical Hele-Shaw cell of width 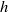. Liquid velocity perturbations induced by the relative movement have also been investigated to analyse the coupling between the bubble motion and the wake dynamics. The confinement ratio 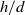is less than unity so that the bubble is flattened between the walls of the cell. As the bubble diameter is increased, the Archimedes and the Bond numbers increase within the ranges 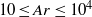and 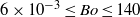. Mean shapes become more and more elongated. They first evolve from in-plane circles to ellipses, then to complicated shapes without fore–aft symmetry and finally to semi-circular-capped bubbles. The scaling law 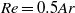is valid for a large range of 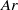, however, indicating that the liquid films between the bubble and the walls do not contribute significantly to the drag force exerted on the bubble. The coupling between wake dynamics, bubble path and shape oscillations evolves and a succession of different regimes of oscillations is observed. The rectilinear bubble motion becomes unstable from a critical value 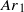through an Hopf bifurcation while the bubble shape is still circular. The amplitude of path oscillations first grows as 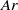increases above 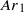but then surprisingly decreases beyond a second Archimedes number 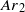. This phenomenon, observed for steady ellipsoidal shape with moderate eccentricity, can be explained by the rapid attenuation of bubble wakes caused by the confinement. Shape oscillations around a significantly elongated mean shape start for 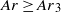. The wake structure progressively evolves due to changes in the bubble shape. After the break-up of the fore–aft symmetry, a fourth regime involving complicated shape oscillations is then observed for 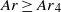. Vortex shedding disappears and unsteady attached vortices coupled to shape oscillations trigger path oscillations of moderate amplitude. Path and shape oscillations finally decrease when 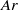is further increased. For 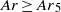, capped bubbles followed by a steady wake rise on a straight path.

JFM classification

Drops and Bubbles: Bubble dynamics Multiphase and Particle-laden Flows: Multiphase flow Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 707 , 25 September 2012 , pp. 444 - 466
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
2. Batchelor, G. K. 1972 Sedimentation in dilute dispersions of spheres. J. Fluid Mech. 52, 245–268.Google Scholar
3. Bessler, W. F. & Littman, H. 1987 Experimental studies of wakes behind circularly capped bubbles. J. Fluid Mech. 185, 137–151.Google Scholar
4. Bush, J. W. M. & Eames, I. 1998 Fluid displacement by high Reynolds number bubble motion in a thin gap. Intl J. Multiphase Flow 24, 3, 411–430.Google Scholar
5. Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops and Particles. Academic.Google Scholar
6. Collins, R. 1965 A simple model of the plane gas bubble in a finite liquid. J. Fluid Mech. 22, 763–771.Google Scholar
7. Ellingsen, K. & Risso, F. 2001 On the rise of an ellipsoidal bubble in water: oscillatory paths and liquid-induced velocity. J. Fluid Mech. 440, 235–268.Google Scholar
8. Fernandes, P., Ern, P., Risso, F. & Magnaudet, J. 2005 On the zigzag dynamics of freely moving axisymmetric bodies. Phys. Fluids 17, 098107.Google Scholar
9. Fernandes, P., Risso, F., Ern, P. & Magnaudet, J. 2007 Oscillatory motion and wake instability of freely rising axisymmetric bodies. J. Fluid Mech. 573, 479–502.Google Scholar
10. Gondret, P. & Rabaud, M. 1997 Shear instability of two-fluid parallel flow in a Hele-Shaw cell. Phys. Fluids 9 (11), 3267–3274.Google Scholar
11. Kelley, E. & Wu, M. 1997 Path instabilities of rising air bubbles in a Hele-Shaw cell. Phys. Rev. Lett. 79, 7, 1265–1268.Google Scholar
12. Lamb, H. 1993 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
13. Lazarek, G. M. & Littman, H. 1974 The pressure field due to large circular capped air bubble rising in water. J. Fluid Mech. 66, 673–687.Google Scholar
14. Lunde, K. & Perkins, R. 1998 Shape oscillations of rising bubbles. Appl. Sci. Res. 58, 387–408.Google Scholar
15. Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32, 659–708.Google Scholar
16. Maruvada, S. R. K. & Park, C. W. 1996 Retarded motion of bubbles in Hele–Shaw cells. Phys. Fluids 8 (12), 3229–3233.Google Scholar
17. Maxworthy, T., Gnann, C., Kürten, M. & Durst, F. 1996 Experiments on the rise of air bubbles in clean viscous liquids. J. Fluid Mech. 321, 421–441.Google Scholar
18. Mougin, G. & Magnaudet, J. 2002 Path instability of a rising bubble. Phys. Rev. Lett. 88, 1, doi:10.1103/PhysRevLett.88.014502.Google Scholar
19. Mougin, G. & Magnaudet, J. 2006 Wake induced forces and torques on a zigzagging/spiralling bubble. J. Fluid Mech. 567, 185–194.Google Scholar
20. Roudet, M., Billet, A. M., Risso, F. & Roig, V. 2011 PIV with volume lighting in a narrow cell: an efficient method to measure large velocity fields of rapidly varying flows. Exp. Therm. Fluid Sci. 35 (6), 1030–1037.Google Scholar
21. Segré, G. & Silberberg, A. 1962 Behaviour of macroscopic rigid spheres in Poiseuille flow. Part 2. Experimental results and interpretation. Phys. Rev. Lett. 14, 136–157.Google Scholar
22. Shew, L., Poncet, S. & Pinton, J. F. 2006 Force measurements on rising bubbles. J. Fluid Mech. 569, 51–60.Google Scholar
23. Taylor, G. I. & Saffman, P. G. 1959 A note on the motion of bubbles in a Hele–Shaw cell and porous medium. Q. J. Mech. Appl. Maths 12, 265–279.Google Scholar
24. Williamson, C. H. K. 1988 Defining an universal and continuous Strouhal–Reynolds number relationship for the laminar vortex shedding of a circular cylinder. Phys. Fluids 31 (10), 2742–2744.Google Scholar