Article contents
Drag reduction in turbulent flows along a cylinder by streamwise-travelling waves of circumferential wall velocity
Published online by Cambridge University Press: 07 January 2019
Abstract
Drag reduction at the external surface of a cylinder in turbulent flows along the axial direction by circumferential wall motion is studied by direct numerical simulations. The circumferential wall oscillation can lead to drag reduction due to the formation of a Stokes layer, but it may also result in centrifugal instability, which can enhance turbulence and increase drag. In the present work, the Reynolds number based on the reference friction velocity and the nominal thickness of the boundary layer is 272. A map describing the relationship between the drag-reduction rate and the control parameters, namely, the angular frequency 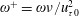 $\unicode[STIX]{x1D714}^{+}=\unicode[STIX]{x1D714}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}0}^{2}$ and the streamwise wavenumber
$\unicode[STIX]{x1D714}^{+}=\unicode[STIX]{x1D714}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}0}^{2}$ and the streamwise wavenumber 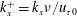 $k_{x}^{+}=k_{x}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}0}$, is obtained at the oscillation amplitude of
$k_{x}^{+}=k_{x}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}0}$, is obtained at the oscillation amplitude of 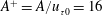 ${A^{+}=A/u}_{\unicode[STIX]{x1D70F}0}=16$, where
${A^{+}=A/u}_{\unicode[STIX]{x1D70F}0}=16$, where 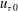 $u_{\unicode[STIX]{x1D70F}0}$ is the friction velocity of the uncontrolled flow and
$u_{\unicode[STIX]{x1D70F}0}$ is the friction velocity of the uncontrolled flow and  $\unicode[STIX]{x1D708}$ is the kinematic viscosity of the fluid. The maximum drag-reduction rate and the maximum drag-increase rate are both approximately 48 %, which are respectively attained at
$\unicode[STIX]{x1D708}$ is the kinematic viscosity of the fluid. The maximum drag-reduction rate and the maximum drag-increase rate are both approximately 48 %, which are respectively attained at 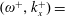 $(\unicode[STIX]{x1D714}^{+},k_{x}^{+})=$ (0.0126, 0.0148) and (0.0246, 0.0018). The drag-reduction rate can be scaled well with the help of the effective thickness of the Stokes layer. The drag increase is observed in a narrow triangular region in the frequency–wavenumber plane. The vortices induced by the centrifugal instability become the primary coherent structure in the near-wall region, and they are closely correlated with the high skin friction. In these drag-increase cases, the effective control frequency or wavenumber is crucial in scaling the drag-increase rate. As the wall curvature normalised by the boundary layer thickness becomes larger, the drag-increase region in the
$(\unicode[STIX]{x1D714}^{+},k_{x}^{+})=$ (0.0126, 0.0148) and (0.0246, 0.0018). The drag-reduction rate can be scaled well with the help of the effective thickness of the Stokes layer. The drag increase is observed in a narrow triangular region in the frequency–wavenumber plane. The vortices induced by the centrifugal instability become the primary coherent structure in the near-wall region, and they are closely correlated with the high skin friction. In these drag-increase cases, the effective control frequency or wavenumber is crucial in scaling the drag-increase rate. As the wall curvature normalised by the boundary layer thickness becomes larger, the drag-increase region in the 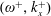 $(\unicode[STIX]{x1D714}^{+},k_{x}^{+})$ plane as well as the maximum drag-increase rate also become larger. Net energy saving with a considerable drag-reduction rate is possible when reducing the oscillation amplitude. At
$(\unicode[STIX]{x1D714}^{+},k_{x}^{+})$ plane as well as the maximum drag-increase rate also become larger. Net energy saving with a considerable drag-reduction rate is possible when reducing the oscillation amplitude. At 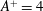 $A^{+}=4$, a net energy saving of 18 % can be achieved with a drag-reduction rate of 25 % if only the power dissipation due to viscous stress is taken into account in an ideal actuation system.
$A^{+}=4$, a net energy saving of 18 % can be achieved with a drag-reduction rate of 25 % if only the power dissipation due to viscous stress is taken into account in an ideal actuation system.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 15
- Cited by




