Article contents
Direct numerical simulation of turbulent channel flow with spanwise rotation
Published online by Cambridge University Press: 22 December 2015
Abstract
A series of direct numerical simulations of turbulent channel flow with spanwise rotation at fixed global friction Reynolds number is performed to investigate the rotation effects on the mean velocity, streamwise velocity fluctuations, Reynolds shear stress and turbulent kinetic energy. The global friction Reynolds number is chosen to be 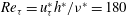 $Re_{{\it\tau}}=u_{{\it\tau}}^{\ast }h^{\ast }/{\it\nu}^{\ast }=180$ (
$Re_{{\it\tau}}=u_{{\it\tau}}^{\ast }h^{\ast }/{\it\nu}^{\ast }=180$ (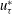 $u_{{\it\tau}}^{\ast }$ is the global friction velocity,
$u_{{\it\tau}}^{\ast }$ is the global friction velocity, 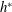 $h^{\ast }$ is the channel half-width and
$h^{\ast }$ is the channel half-width and 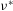 ${\it\nu}^{\ast }$ is the kinematic viscosity), while the global-friction-velocity-based rotation number
${\it\nu}^{\ast }$ is the kinematic viscosity), while the global-friction-velocity-based rotation number 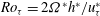 $Ro_{{\it\tau}}=2{\it\Omega}^{\ast }h^{\ast }/u_{{\it\tau}}^{\ast }$ (
$Ro_{{\it\tau}}=2{\it\Omega}^{\ast }h^{\ast }/u_{{\it\tau}}^{\ast }$ (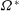 ${\it\Omega}^{\ast }$ is the dimensional angular velocity) varies from 0 to 130. In the previously reported
${\it\Omega}^{\ast }$ is the dimensional angular velocity) varies from 0 to 130. In the previously reported 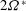 $2{\it\Omega}^{\ast }$-slope region for the mean velocity, a linear behaviour for the streamwise velocity fluctuations, a unit-slope linear profile for the Reynolds shear stress and a
$2{\it\Omega}^{\ast }$-slope region for the mean velocity, a linear behaviour for the streamwise velocity fluctuations, a unit-slope linear profile for the Reynolds shear stress and a 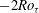 $-2Ro_{{\it\tau}}$-slope linear profile for the production term of
$-2Ro_{{\it\tau}}$-slope linear profile for the production term of 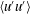 $\langle u^{\prime }u^{\prime }\rangle$ have been identified for the first time. The critical rotation number, which corresponds to the laminar limit, is predicted to be equal to
$\langle u^{\prime }u^{\prime }\rangle$ have been identified for the first time. The critical rotation number, which corresponds to the laminar limit, is predicted to be equal to 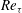 $Re_{{\it\tau}}$ according to the unit-slope linear profile of the Reynolds shear stress. Our results also show that a parabolic profile of the mean velocity can be identified around the ‘second plateau’ region of the Reynolds shear stress for
$Re_{{\it\tau}}$ according to the unit-slope linear profile of the Reynolds shear stress. Our results also show that a parabolic profile of the mean velocity can be identified around the ‘second plateau’ region of the Reynolds shear stress for 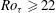 $Ro_{{\it\tau}}\geqslant 22$. The parabolas at different rotation numbers have the same shape of
$Ro_{{\it\tau}}\geqslant 22$. The parabolas at different rotation numbers have the same shape of 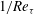 $1/Re_{{\it\tau}}$, the radius of curvature at the vertex. Furthermore, the system rotation increases the volume-averaged turbulent kinetic energy at lower rotation rates, and then decreases it when
$1/Re_{{\it\tau}}$, the radius of curvature at the vertex. Furthermore, the system rotation increases the volume-averaged turbulent kinetic energy at lower rotation rates, and then decreases it when 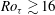 $Ro_{{\it\tau}}\gtrsim 16$.
$Ro_{{\it\tau}}\gtrsim 16$.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 38
- Cited by





