Article contents
Direct numerical simulation of free convection over a heated plate
Published online by Cambridge University Press: 08 October 2012
Abstract
Direct numerical simulations of free convection over a smooth, heated plate are used to investigate unbounded, unsteady turbulent convection. Four different boundary conditions are considered: free-slip or no-slip walls, and constant buoyancy or constant buoyancy flux. It is first shown that, after the initial transient, the vertical structure agrees with observations in the atmospheric boundary layer and predictions from classical similarity theory. A quasi-steady inner layer and a self-preserving outer layer are clearly distinguished, with an overlap region between them of constant turbulent buoyancy flux. The extension of the overlap region reached in our simulations is more than 100 wall units 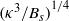 $ \mathop{ ({\kappa }^{3} / {B}_{s} )}\nolimits ^{1/ 4} $, where
$ \mathop{ ({\kappa }^{3} / {B}_{s} )}\nolimits ^{1/ 4} $, where 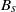 ${B}_{s} $ is the surface buoyancy flux and
${B}_{s} $ is the surface buoyancy flux and  $\kappa $ the corresponding molecular diffusivity (the Prandtl number is one). The buoyancy fluctuation inside the overlap region already exhibits the
$\kappa $ the corresponding molecular diffusivity (the Prandtl number is one). The buoyancy fluctuation inside the overlap region already exhibits the  $\ensuremath{-} 1/ 3$ power-law scaling with height for the four types of boundary conditions, as expected in the local, free-convection regime. However, the mean buoyancy gradient and the vertical velocity fluctuation are still evolving toward the corresponding power laws predicted by the similarity theory. The second major result is that the relation between the Nusselt and Rayleigh numbers agrees with that reported in Rayleigh–Bénard convection when the heated plate is interpreted as half a convection cell. The range of Rayleigh numbers covered in the simulations is then
$\ensuremath{-} 1/ 3$ power-law scaling with height for the four types of boundary conditions, as expected in the local, free-convection regime. However, the mean buoyancy gradient and the vertical velocity fluctuation are still evolving toward the corresponding power laws predicted by the similarity theory. The second major result is that the relation between the Nusselt and Rayleigh numbers agrees with that reported in Rayleigh–Bénard convection when the heated plate is interpreted as half a convection cell. The range of Rayleigh numbers covered in the simulations is then 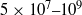 $5\ensuremath{\times} 1{0}^{7} \text{{\ndash}} 1{0}^{9} $. Further analogies between the two problems indicate that knowledge can be transferred between steady Rayleigh–Bénard and unsteady convection. Last, we find that the inner scaling based on
$5\ensuremath{\times} 1{0}^{7} \text{{\ndash}} 1{0}^{9} $. Further analogies between the two problems indicate that knowledge can be transferred between steady Rayleigh–Bénard and unsteady convection. Last, we find that the inner scaling based on 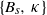 $\{ {B}_{s} , \hspace{0.167em} \kappa \} $ reduces the effect of the boundary conditions to, mainly, the diffusive wall layer, the first 10 wall units. There, near the plate, free-slip conditions allow stronger mixing than no-slip ones, which results in 30 % less buoyancy difference between the surface and the overlap region and 30–40 % thinner diffusive sublayers. However, this local effect also entails one global, substantial effect: with an imposed buoyancy, free-slip systems develop a surface flux 60 % higher than that obtained with no-slip walls, which implies more intense turbulent fluctuations across the whole boundary layer and a faster growth.
$\{ {B}_{s} , \hspace{0.167em} \kappa \} $ reduces the effect of the boundary conditions to, mainly, the diffusive wall layer, the first 10 wall units. There, near the plate, free-slip conditions allow stronger mixing than no-slip ones, which results in 30 % less buoyancy difference between the surface and the overlap region and 30–40 % thinner diffusive sublayers. However, this local effect also entails one global, substantial effect: with an imposed buoyancy, free-slip systems develop a surface flux 60 % higher than that obtained with no-slip walls, which implies more intense turbulent fluctuations across the whole boundary layer and a faster growth.
JFM classification
- Type
- Papers
- Information
- Copyright
- ©2012 Cambridge University Press
References
- 45
- Cited by




