Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Esmaily, M.
and
Horwitz, J.A.K.
2018.
A correction scheme for two-way coupled point-particle simulations on anisotropic grids.
Journal of Computational Physics,
Vol. 375,
Issue. ,
p.
960.
Weiss, Philipp
Meyer, Daniel W.
and
Jenny, Patrick
2018.
Evaporating droplets in turbulence studied with statistically stationary homogeneous direct numerical simulation.
Physics of Fluids,
Vol. 30,
Issue. 8,
Horwitz, J.A.K.
and
Mani, A.
2018.
Correction scheme for point-particle models applied to a nonlinear drag law in simulations of particle-fluid interaction.
International Journal of Multiphase Flow,
Vol. 101,
Issue. ,
p.
74.
Fong, Kee Onn
Amili, Omid
and
Coletti, Filippo
2019.
Velocity and spatial distribution of inertial particles in a turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 872,
Issue. ,
p.
367.
Zhao, Lihao
Challabotla, Niranjan R.
Andersson, Helge I.
and
Variano, Evan A.
2019.
Mapping spheroid rotation modes in turbulent channel flow: effects of shear, turbulence and particle inertia.
Journal of Fluid Mechanics,
Vol. 876,
Issue. ,
p.
19.
Balachandar, S.
Liu, Kai
and
Lakhote, Mandar
2019.
Self-induced velocity correction for improved drag estimation in Euler–Lagrange point-particle simulations.
Journal of Computational Physics,
Vol. 376,
Issue. ,
p.
160.
Schneiders, Lennart
Fröhlich, Konstantin
Meinke, Matthias
and
Schröder, Wolfgang
2019.
The decay of isotropic turbulence carrying non-spherical finite-size particles.
Journal of Fluid Mechanics,
Vol. 875,
Issue. ,
p.
520.
Innocenti, A.
Fox, R. O.
Salvetti, M. V.
and
Chibbaro, S.
2019.
A Lagrangian probability-density-function model for collisional turbulent fluid–particle flows.
Journal of Fluid Mechanics,
Vol. 862,
Issue. ,
p.
449.
Fukada, Toshiaki
Takeuchi, Shintaro
and
Kajishima, Takeo
2019.
Estimation of fluid forces on a spherical particle for two-way coupling simulation based on the volume averaging.
International Journal of Multiphase Flow,
Vol. 113,
Issue. ,
p.
165.
Subramaniam, Shankar
2020.
Multiphase flows: Rich physics, challenging theory, and big simulations.
Physical Review Fluids,
Vol. 5,
Issue. 11,
Kumaran, V.
Muramulla, N. S. P.
Tyagi, A.
and
Goswami, P. S.
2020.
Turbulence collapses at a threshold particle loading in a dilute particle-gas suspension.
EPL (Europhysics Letters),
Vol. 128,
Issue. 6,
p.
64001.
Lattanzi, Aaron M.
Yin, Xiaolong
and
Hrenya, Christine M.
2020.
Heat and momentum transfer to a particle in a laminar boundary layer.
Journal of Fluid Mechanics,
Vol. 889,
Issue. ,
Chen, Songying
Chen, Xiaohang
Wan, Dongdong
Sun, Xun
Ji, Li
Wu, Ke
Yang, Fan
and
Wang, Guichao
2020.
Particle-resolved direct numerical simulation of collisions of bidisperse inertial particles in a homogeneous isotropic turbulence.
Powder Technology,
Vol. 376,
Issue. ,
p.
72.
Muramulla, P.
Tyagi, A.
Goswami, P. S.
and
Kumaran, V.
2020.
Disruption of turbulence due to particle loading in a dilute gas–particle suspension.
Journal of Fluid Mechanics,
Vol. 889,
Issue. ,
Horwitz, J. A. K.
and
Mani, A.
2020.
Two-way coupled particle-turbulence interaction: Effect of numerics and resolution on fluid and particle statistics.
Physical Review Fluids,
Vol. 5,
Issue. 10,
Fukada, Toshiaki
Takeuchi, Shintaro
and
Kajishima, Takeo
2020.
Anisotropic Reaction Force Model in Two-way Coupling Simulation for a Smaller Particle Than Grid Spacing Based on Volume Averaging.
Flow, Turbulence and Combustion,
Vol. 105,
Issue. 4,
p.
1017.
Pakseresht, Pedram
Esmaily, Mahdi
and
Apte, Sourabh V.
2020.
A correction scheme for wall-bounded two-way coupled point-particle simulations.
Journal of Computational Physics,
Vol. 420,
Issue. ,
p.
109711.
Paul, Immanuvel
Bassenne, Maxime
and
Mani, Ali
2020.
A filtering strategy for the numerical convergence of radiation transport through purely absorbing particle clouds.
Journal of Quantitative Spectroscopy and Radiative Transfer,
Vol. 247,
Issue. ,
p.
106941.
Costa, Pedro
Brandt, Luca
and
Picano, Francesco
2020.
Interface-resolved simulations of small inertial particles in turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 883,
Issue. ,
Li, Zhenzhong
Wei, Jinjia
Bu, Shanshan
and
Yu, Bo
2021.
A Frequency Analysis Method to Estimate the Relative Importance of Basset Force on Small Particles in Turbulence.
International Journal of Multiphase Flow,
Vol. 139,
Issue. ,
p.
103640.
 $\unicode[STIX]{x1D719}=0.001$ in a decaying isotropic turbulent particle-laden flow. The particle diameter
$\unicode[STIX]{x1D719}=0.001$ in a decaying isotropic turbulent particle-laden flow. The particle diameter 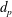 $d_{p}$ in the suspension is chosen to be the same as the initial Kolmogorov length scale
$d_{p}$ in the suspension is chosen to be the same as the initial Kolmogorov length scale 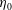 $\unicode[STIX]{x1D702}_{0}$ (
$\unicode[STIX]{x1D702}_{0}$ (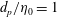 $d_{p}/\unicode[STIX]{x1D702}_{0}=1$) in order to overlap with the regime where PP-DNS is valid. We assess the point-particle acceleration model for two different particle Stokes numbers,
$d_{p}/\unicode[STIX]{x1D702}_{0}=1$) in order to overlap with the regime where PP-DNS is valid. We assess the point-particle acceleration model for two different particle Stokes numbers, 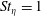 $St_{\unicode[STIX]{x1D702}}=1$ and 100. For the high Stokes number case, the Stokes drag model for particle acceleration under-predicts the true particle acceleration. In addition, second moment quantities which play key roles in the physical evolution of the gas–solid suspension are not correctly captured. Considering finite Reynolds number corrections to the acceleration model improves the prediction of the particle acceleration probability density function and second moment statistics of the point-particle model compared with the particle-resolved simulation. We also find that accounting for the undisturbed fluid velocity in the acceleration model can be of greater importance than using the most appropriate acceleration model for a given physical problem.
$St_{\unicode[STIX]{x1D702}}=1$ and 100. For the high Stokes number case, the Stokes drag model for particle acceleration under-predicts the true particle acceleration. In addition, second moment quantities which play key roles in the physical evolution of the gas–solid suspension are not correctly captured. Considering finite Reynolds number corrections to the acceleration model improves the prediction of the particle acceleration probability density function and second moment statistics of the point-particle model compared with the particle-resolved simulation. We also find that accounting for the undisturbed fluid velocity in the acceleration model can be of greater importance than using the most appropriate acceleration model for a given physical problem.




