Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-26T09:45:33.125Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuum perspective of bulk viscosity in compressible fluids

Published online by Cambridge University Press:  11 January 2017

Xin-Dong Li ,
Zong-Min Hu  and
Zong-Lin Jiang
Xin-Dong Li
Affiliation:
State Key Laboratory of High Temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
Zong-Min Hu*
Affiliation:
State Key Laboratory of High Temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
Zong-Lin Jiang
Affiliation:
State Key Laboratory of High Temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
*
†Email address for correspondence: huzm@imech.ac.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

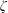Kinetic theory and acoustic measurements have proven that the bulk viscosity associated with the expansion or compression effect cannot be ignored in compressible fluids except for monatomic gases. A new theoretical formula for the bulk viscosity coefficient (BVC) $\unicode[STIX]{x1D701}$ is derived by the continuum medium methodology, which provides a further understanding of the bulk viscosity, i.e. 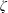$\unicode[STIX]{x1D701}$ is equal to the product of the bulk modulus 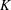$K$ and the relaxation time $\unicode[STIX]{x1D70F}$ (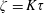$\unicode[STIX]{x1D701}=K\unicode[STIX]{x1D70F}$). The continuum and kinetic theories present consistent results from macro- and microperspectives respectively, only differing in terms of a coefficient. 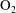The theoretical predictions of the BVC in diatomic molecules, such as $\text{N}_{2}$, $\text{O}_{2}$ and CO, show good agreement with the experimental data over a wide range of temperature. In addition, the vibrational contributions to 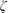$\unicode[STIX]{x1D701}$ are controlled by a rapid exponential decrease at high temperatures, while at low temperatures a slow linear increase proceeds for the rotational cases. The relaxation time $\unicode[STIX]{x1D70F}$, collision number 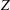$Z$, BVC 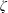$\unicode[STIX]{x1D701}$ and ratio of bulk-to-shear viscosities $\unicode[STIX]{x1D701}/\unicode[STIX]{x1D707}$ in the vibrational mode are found to be several orders of magnitude larger than those in the rotational mode.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Gas dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 812 , 10 February 2017 , pp. 966 - 990
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J. D. 2006 Hypersonic and High-Temperature Gas Dynamics, 2nd edn. AIAA.CrossRefGoogle Scholar
Bahmani, F. & Cramer, M. S. 2014 Suppression of shock-induced separation in fluids having large bulk viscosities. J. Fluid Mech. 756, 1–10.CrossRefGoogle Scholar
Bauer, H. J. & Kosche, H. 1966 Rotational relaxation in carbon monoxide compared with other diatomic gases. Acustica 17 (2), 96–97.Google Scholar
Billet, G., Giovangigli, V. & Gassowski, G. D. 2008 Impact of volume viscosity on a shock/hydrogen bubble interaction. Combust. Theor. Model. 12 (2), 221–248.CrossRefGoogle Scholar
Blackman, V. 1956 Vibrational relaxation in oxygen and nitrogen. J. Fluid Mech. 1 (1), 61–85.CrossRefGoogle Scholar
Borgnakke, C. & Sonntag, R. E. 2009 Fundamentals of Thermodynamics. Wiley.Google Scholar
Carnevale, E. H., Carey, C. & Larson, G. 1967 Ultrasonic determination of rotational collision numbers and vibrational relaxation times of polyatomic gases at high temperatures. J. Chem. Phys. 27 (8), 2829–2835.CrossRefGoogle Scholar
Chapman, S. & Cowling, T. G. 1970 The Mathematical Theory of Non-uniform Gases, 3rd edn. Cambridge University Press.Google Scholar
Chikitkin, A. V., Rogov, B. V., Tirsky, G. A. & Utyuzhnikov, S. V. 2015 Effect of bulk viscosity in supersonic flow past spacecraft. Appl. Numer. Maths 93, 47–60.CrossRefGoogle Scholar
Cramer, M. S. 2012 Numerical estimates for the bulk viscosity of ideal gases. Phys. Fluids 24, 066102.CrossRefGoogle Scholar
Cramer, M. S. & Bahmani, F. 2014 Effect of large bulk viscosity on large-Reynolds-number flows. J. Fluid Mech. 751, 142–163.CrossRefGoogle Scholar
Connor, J. V. 1958 Ultrasonic dispersion in oxygen. J. Acoust. Soc. Am. 30 (4), 297–300.CrossRefGoogle Scholar
Elizarova, T. G., Khokhlov, A. A. & Montero, S. 2007 Numerical simulation of shock wave structure in nitrogen. Phys. Fluids 19, 068102.CrossRefGoogle Scholar
Emanuel, G. 1990 Bulk viscosity of a dilute polyatomic gas. Phys. Fluids 2, 2252–2254.CrossRefGoogle Scholar
Emanuel, G. 1992 Effect of bulk viscosity on a hypersonic boundary layer. Phys. Fluids 4, 491–495.CrossRefGoogle Scholar
Emanuel, G. 1994 Linear dependence of the bulk viscosity on shock wave thickness. Phys. Fluids 6, 3202–3205.CrossRefGoogle Scholar
Emanuel, G. 1998 Bulk viscosity in the Navier–Stokes equations. Intl J. Engng Sci. 36 (11), 1313–1323.CrossRefGoogle Scholar
Emanuel, G. 2016 Analytical Fluid Dynamics, 3rd edn. CRC Press.Google Scholar
Eringen, A. C. 1980 Mechanics of Continua, 2nd edn. Krieger.Google Scholar
Fru, G., Janiga, G. & Thevenin, D. 2011 Direct numerical simulations of the impact of high turbulence intensities and volume viscosity on premixed methane flames. J. Combust. 2011, 746719.Google Scholar
Fru, G., Janiga, G. & Thevenin, D. 2012 Impact of volume viscosity on the structure of turbulent premixed flames in the thin reaction zone regime. Flow Turbul. Combust. 88, 451–478.CrossRefGoogle Scholar
Fujii, Y., Lindsay, R. B. & Urushihara, K. 1963 Ultrasonic absorption and relaxation times in nitrogen, oxygen, and water vapor. J. Acoust. Soc. Am. 35 (7), 961–966.CrossRefGoogle Scholar
Gaydon, A. G. & Hurle, I. R.1961 Measurement of times of vibrational relaxation and dissociation behind shock waves in $\text{N}_{2}$ , $\text{O}_{2}$ , air, CO, $\text{CO}_{2}$ and $\text{H}_{2}$ . Tech. Rep. 309-318; 8th Symp. Combust.CrossRefGoogle Scholar
Gonzalez, H. & Emanuel, G. 1993 Effect of bulk viscosity on Couette flow. Phys. Fluids 5, 1267–1268.CrossRefGoogle Scholar
Graves, R. E. & Argrow, B. M. 1999 Bulk viscosity: past to present. J. Thermophys. Heat Transfer 13 (3), 337–342.CrossRefGoogle Scholar
Greenspan, M. 1959 Rotational relaxation in nitrogen, oxygen, and air. J. Acoust. Soc. Am. 31 (2), 155–160.CrossRefGoogle Scholar
Henderson, M. C. 1962 Vibrational relaxation in nitrogen and other gases. J. Acoust. Soc. Am. 34, 349–350.CrossRefGoogle Scholar
Herzfeld, K. F. & Litovitz, T. A. 1959 Absorption and Dispersion of Ultrasonic Waves. Academic.Google Scholar
Holmes, R., Jones, G. R., Pusat, N. & Tempest, W. 1962 Rotational relaxation in helium + oxygen and helium + nitrogen mixtures. Trans. Farad. Soc. 58, 2342–2347.CrossRefGoogle Scholar
Holmes, R., Simth, F. A. & Tempest, W. 1963 Vibrational relaxation in oxygen. Proc. Phys. Soc. 81 (2), 311–319.CrossRefGoogle Scholar
Hooker, W. J. & Millikan, R. C. 1963 Shock-tube study of vibrational relaxation in carbon monoxide for the fundamental and first overtone. J. Chem. Phys. 38 (1), 214–220.CrossRefGoogle Scholar
Hurle, L. R. 1964 Line-reversal studies of the sodium excitation process behind shock waves in N2 . J. Chem. Phys. 41 (12), 3911–3920.CrossRefGoogle Scholar
Kistemaker, P. G., Tom, A. & Vries, A. E. D. 1970 Rotational relaxation numbers for the isotopic molecules of N2 and CO. Physica 48, 414–424.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics, 2nd edn. Pergamon.Google Scholar
Lukasik, S. J. & Young, J. E. 1957 Vibrational relaxation times in nitrogen. J. Chem. Phys. 27 (5), 1149–1155.CrossRefGoogle Scholar
Matthews, D. L. 1961 Vibrational relaxation of carbon monoxide in the shock tube. J. Chem. Phys. 34 (2), 639–642.CrossRefGoogle Scholar
Michel, A. A. 1985 Compressible Fluid Flow. Prentice-Hall.Google Scholar
Millikan, R. C. & White, D. R. 1963a Vibrational energy exchange between N2 and CO. The vibrational relaxation of nitrogen. J. Chem. Phys. 39 (1), 98–101.CrossRefGoogle Scholar
Millikan, R. C. & White, D. R. 1963b Systematic of vibrational relaxation. J. Chem. Phys. 39 (12), 3209–3213.CrossRefGoogle Scholar
Monchick, L., Yun, K. S. & Mason, E. A. 1963 Formal kinetic theory of transport phenomena in polyatomic gas mixtures. J. Chem. Phys. 39 (3), 654–669.CrossRefGoogle Scholar
Parker, J. G. 1959 Rotational and vibrational relaxation in diatomic gases. Phys. Fluids 2 (4), 449–462.CrossRefGoogle Scholar
Parker, J. G. 1961 Effect of several light molecules on the vibrational relaxation time of oxygen. J. Chem. Phys. 34 (5), 1763–1772.CrossRefGoogle Scholar
Parker, J. G. 1964 Comparison of experimental and theoretical vibrational relaxation times for diatomic gases. J. Chem. Phys. 41 (6), 1600–1609.CrossRefGoogle Scholar
Parker, J. G., Adams, C. E. & Stavseth, R. M. 1953 Absorption of sound in argon, nitrogen, and oxygen at low pressure. J. Acoust. Soc. Am. 25 (2), 263–269.CrossRefGoogle Scholar
Prangsma, G. J., Alberga, A. H. & Beenakker, J. J. M. 1973 Ultrasonic determination of the volume viscosity of N2 , CO, CH4 and CD4 between 77 and 300 K. Physica 64 (2), 278–288.CrossRefGoogle Scholar
Rajagopal, K. R. 2013 A new development and interpretation of the Navier–Stokes fluid which reveals why the ‘Stokes assumption’ is inapt. Intl J. Non-Linear Mech. 50, 141–151.CrossRefGoogle Scholar
Sherman, F. S.1955 A low-density wind-tunnel study of shock-wave structure and relaxation phenomena in gases. NACA Tech. Rep. TN-3298.Google Scholar
Shileds, F. D. & Lee, K. P. 1963 Sound absorption and velocity measurements in oxygen. J. Acoust. Soc. Am. 35, 251–252.CrossRefGoogle Scholar
Sivian, L. J. 1947 High frequency absorption in air and other gases. J. Acoust. Soc. Am. 19 (5), 914–916.CrossRefGoogle Scholar
Smith, F. A. & Tempest, W. 1961 Low-frequency sound propagation in gases. J. Acoust. Soc. Am. 33, 1626–1627.CrossRefGoogle Scholar
Stokes, G. G. 1845 On the theories of the internal friction of fluids in motion, and of the equilibrium and motion of elastic solids. Trans. Camb. Phil. Soc. 8 (22), 287–342.Google Scholar
Tempest, W. T. & Parbrook, H. D. 1957 The absorption of sound in argon, nitrogen and oxygen. Acustica 7 (6), 354–362.Google Scholar
Thompson, P. A. 1972 Compressible-Fluid Dynamics. McGraw-Hill.CrossRefGoogle Scholar
Tip, A., Los, J. & Vries, A. E. D. 1967 Rotational relaxation numbers from thermal transpiration measurements. Physica 35, 489–498.CrossRefGoogle Scholar
Tisza, L. 1942 Supersonic absorption and Stokes’ viscosity relation. Phys. Rev. 61, 531–536.CrossRefGoogle Scholar
Vincenti, W. G. & Kruger, G. H. 1965 Introduction to Physical Gas Dynamics. Krieger.Google Scholar
Wang, C. & Uhlenbeck, G. E.1951 Transport phenomena in polyatomic gases. Tech. Rep. CM-681. US Navy Department.Google Scholar
White, D. R. & Millikan, R. C. 1963 Vibrational relaxation of oxygen. J. Chem. Phys. 39 (1), 1803–1806.CrossRefGoogle Scholar
Windsor, M. W., Davidson, N. & Taylor, R. 1957 Measurement of the vibrational relaxation time of CO behind a shock wave by infrared emission. J. Chem. Phys. 27, 315–316.CrossRefGoogle Scholar
Winter, T. G. & Hill, G. 1967 High-temperature ultrasonic measurements of rotational relaxation in hydrogen, deuterium, nitrogen, and oxygen. J. Acoust. Soc. Am. 42 (4), 848–858.CrossRefGoogle Scholar
Zartman, I. F. 1949 Ultrasonic velocities and absorption in gases at low pressures. J. Acoust. Soc. Am. 21 (3), 171–174.CrossRefGoogle Scholar
Zel’dovich, Y. B. & Raizer, Y. P. 1966 Physics of Shock Waves and High-Temperature Hydrodynamics Phenomena, vol. 2. Academic.Google Scholar
Zmuda, A. J. 1951 Dispersion of velocity and anomalous absorption of ultrasonics in nitrogen. J. Acoust. Soc. Am. 23 (4), 472–477.CrossRefGoogle Scholar