Article contents
Confined turbulent entrainment across density interfaces
Published online by Cambridge University Press: 14 August 2015
Abstract
In pursuit of a universal law for the rate of entrainment across a density interface driven by the impingement of a localised turbulent flow, the role of the confinement, wherein the environment is within the confines of a box, has to date been overlooked. Seeking to unravel the effects of confinement, we develop a phenomenological model describing the quasi-steady rate at which buoyant fluid is turbulently entrained across a density interface separating two uniform layers within the confines of a box. The upper layer is maintained by a turbulent plume, and the localised impingement of a turbulent fountain with the interface drives entrainment of fluid from the upper layer into the lower layer. The plume and fountain rise from sources at the base of the box and are non-interacting. Guided by previous observations, our model characterises the dynamics of fountain–interface interaction and the steady secondary flow in the environment that is induced by the perpetual cycle of vertical excursions of the interface. We reveal that the dimensionless entrainment flux across the interface 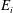 $E_{i}$ is governed not only by an interfacial Froude number
$E_{i}$ is governed not only by an interfacial Froude number 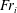 $\mathit{Fr}_{i}$ but also by a ‘confinement’ parameter
$\mathit{Fr}_{i}$ but also by a ‘confinement’ parameter 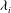 ${\it\lambda}_{i}$, which characterises the length scale of interfacial turbulence relative to the depth of the upper layer. By deducing the range of
${\it\lambda}_{i}$, which characterises the length scale of interfacial turbulence relative to the depth of the upper layer. By deducing the range of  ${\it\lambda}_{i}$ that may be regarded as ‘small’ and ‘large’, we shed new light on the effects of confinement on interfacial entrainment. We establish that for small
${\it\lambda}_{i}$ that may be regarded as ‘small’ and ‘large’, we shed new light on the effects of confinement on interfacial entrainment. We establish that for small 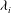 ${\it\lambda}_{i}$, a weak secondary flow has little influence on
${\it\lambda}_{i}$, a weak secondary flow has little influence on 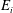 $E_{i}$, which follows a quadratic power law
$E_{i}$, which follows a quadratic power law  $E_{i}\propto \mathit{Fr}_{i}^{2}$. For large
$E_{i}\propto \mathit{Fr}_{i}^{2}$. For large 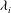 ${\it\lambda}_{i}$, a strong secondary flow significantly influences
${\it\lambda}_{i}$, a strong secondary flow significantly influences  $E_{i}$, which then follows a cubic power law
$E_{i}$, which then follows a cubic power law 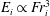 $E_{i}\propto \mathit{Fr}_{i}^{3}$. Drawing on these results, and showing that for previous experimental studies
$E_{i}\propto \mathit{Fr}_{i}^{3}$. Drawing on these results, and showing that for previous experimental studies 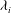 ${\it\lambda}_{i}$ exhibits wide variation, we highlight underlying physical reasons for the significant scatter in the existing measurements of the rate of interfacial entrainment. Finally, we explore the implications of our results for guiding appropriate choices of box geometry for experimentally and numerically examining interfacial entrainment.
${\it\lambda}_{i}$ exhibits wide variation, we highlight underlying physical reasons for the significant scatter in the existing measurements of the rate of interfacial entrainment. Finally, we explore the implications of our results for guiding appropriate choices of box geometry for experimentally and numerically examining interfacial entrainment.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 10
- Cited by





