Article contents
The common mechanism of turbulent skin-friction drag reduction with superhydrophobic longitudinal microgrooves and riblets
Published online by Cambridge University Press: 10 January 2018
Abstract
Turbulent skin-friction drag reduction with superhydrophobic (SH) longitudinal microgrooves and riblets is investigated by direct numerical simulation (DNS), using lattice Boltzmann methods, in channel flow. The liquid/gas interfaces in the SH longitudinal microgrooves were modelled as stationary, curved, shear-free boundaries, with the meniscus shape determined from the solution of the Young–Laplace equation. Interface protrusion angles of 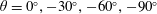 $\unicode[STIX]{x1D703}=0^{\circ },-30^{\circ },-60^{\circ },-90^{\circ }$ were investigated. For comparison, the same geometries as those formed by the SH interfaces were also studied as riblets. Drag reductions of up to 61 % and up to 5 % were realized in DNS with SH longitudinal microgrooves and riblets, respectively, in turbulent channel flows at bulk Reynolds numbers of
$\unicode[STIX]{x1D703}=0^{\circ },-30^{\circ },-60^{\circ },-90^{\circ }$ were investigated. For comparison, the same geometries as those formed by the SH interfaces were also studied as riblets. Drag reductions of up to 61 % and up to 5 % were realized in DNS with SH longitudinal microgrooves and riblets, respectively, in turbulent channel flows at bulk Reynolds numbers of 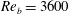 $Re_{b}=3600$ (
$Re_{b}=3600$ (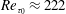 $Re_{\unicode[STIX]{x1D70F}_{0}}\approx 222$) and
$Re_{\unicode[STIX]{x1D70F}_{0}}\approx 222$) and 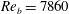 $Re_{b}=7860$ (
$Re_{b}=7860$ (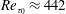 $Re_{\unicode[STIX]{x1D70F}_{0}}\approx 442$), with arrays of SH longitudinal microgrooves or riblets of size
$Re_{\unicode[STIX]{x1D70F}_{0}}\approx 442$), with arrays of SH longitudinal microgrooves or riblets of size 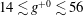 $14\lesssim g^{+0}\lesssim 56$ and
$14\lesssim g^{+0}\lesssim 56$ and 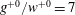 $g^{+0}/w^{+0}=7$ on both walls, where
$g^{+0}/w^{+0}=7$ on both walls, where 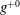 $g^{+0}$ and
$g^{+0}$ and 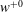 $w^{+0}$ denote the widths and spacings of the microgrooves in base flow wall units, respectively. An exact analytical expression is derived which allows the net drag reduction in laminar or turbulent channel flow with any SH or no-slip wall micro-texture to be decomposed into contributions from: (i) the effective slip velocity at the wall, (ii) modifications to the normalized structure of turbulent Reynolds shear stresses due to the presence of this effective slip velocity at the wall, (iii) other modifications to the normalized structure of turbulent Reynolds shear stresses due to the presence of the wall micro-texture, (iv) modifications to the normalized structure of mean flow shear stresses due to the presence of the wall micro-texture and (v) the fraction of the flow rate through the wall micro-texture. Comparison to DNS results shows that SH longitudinal microgrooves and riblets share a common mechanism of drag reduction in which
$w^{+0}$ denote the widths and spacings of the microgrooves in base flow wall units, respectively. An exact analytical expression is derived which allows the net drag reduction in laminar or turbulent channel flow with any SH or no-slip wall micro-texture to be decomposed into contributions from: (i) the effective slip velocity at the wall, (ii) modifications to the normalized structure of turbulent Reynolds shear stresses due to the presence of this effective slip velocity at the wall, (iii) other modifications to the normalized structure of turbulent Reynolds shear stresses due to the presence of the wall micro-texture, (iv) modifications to the normalized structure of mean flow shear stresses due to the presence of the wall micro-texture and (v) the fraction of the flow rate through the wall micro-texture. Comparison to DNS results shows that SH longitudinal microgrooves and riblets share a common mechanism of drag reduction in which 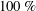 $100\,\%$ of the drag reduction arises from effects (i) and (ii). The contributions from (iii)–(v) were always drag enhancing, and followed a common scaling with SH longitudinal microgrooves and riblets when expressed as a function of the square root of the microgroove cross-sectional area in wall units. Extrapolation of drag reduction data from DNS to high Reynolds number flows of practical interest is discussed. It is shown that, for a given geometry and size of the surface micro-texture in wall units, the drag reduction performance of micro-textured surfaces degrades with increasing bulk Reynolds number of the flow. Curved SH interfaces at low protrusion angle (
$100\,\%$ of the drag reduction arises from effects (i) and (ii). The contributions from (iii)–(v) were always drag enhancing, and followed a common scaling with SH longitudinal microgrooves and riblets when expressed as a function of the square root of the microgroove cross-sectional area in wall units. Extrapolation of drag reduction data from DNS to high Reynolds number flows of practical interest is discussed. It is shown that, for a given geometry and size of the surface micro-texture in wall units, the drag reduction performance of micro-textured surfaces degrades with increasing bulk Reynolds number of the flow. Curved SH interfaces at low protrusion angle (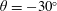 $\unicode[STIX]{x1D703}=-30^{\circ }$) were found to enhance the drag reduction by up to 3.6 % compared to flat interfaces, while reducing the instantaneous pressure fluctuations on the SH interfaces by up to a factor of two. This suggests that the longevity of SH interfaces in turbulent flow may be improved by embedding the SH surface within the microgrooves of shallow, scalloped riblets.
$\unicode[STIX]{x1D703}=-30^{\circ }$) were found to enhance the drag reduction by up to 3.6 % compared to flat interfaces, while reducing the instantaneous pressure fluctuations on the SH interfaces by up to a factor of two. This suggests that the longevity of SH interfaces in turbulent flow may be improved by embedding the SH surface within the microgrooves of shallow, scalloped riblets.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 68
- Cited by





