Hostname: page-component-848d4c4894-xfwgj Total loading time: 0 Render date: 2024-06-22T06:28:32.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Coherent structures and the saturation of a nonlinear dynamo

Published online by Cambridge University Press:  19 July 2013

Erico L. Rempel ,
Abraham C.-L. Chian ,
Axel Brandenburg ,
Pablo R. Muñoz  and
Shawn C. Shadden
Erico L. Rempel*
Affiliation:
Institute of Aeronautical Technology (ITA), World Institute for Space Environment Research (WISER), 12228–900 São José dos Campos – SP, Brazil
Abraham C.-L. Chian
Affiliation:
Institute of Aeronautical Technology (ITA), World Institute for Space Environment Research (WISER), 12228–900 São José dos Campos – SP, Brazil Observatoire de Paris, LESIA, CNRS, 92190 Meudon, France National Institute for Space Research (INPE), WISER, P.O. Box 515, 12227–010 São José dos Campos – SP, Brazil
Axel Brandenburg
Affiliation:
NORDITA, KTH Royal Institute of Technology and Stockholm University, Roslagstullsbacken 23, SE 10691 Stockholm, Sweden Department of Astronomy, Stockholm University, SE 10691 Stockholm, Sweden
Pablo R. Muñoz
Affiliation:
Institute of Aeronautical Technology (ITA), World Institute for Space Environment Research (WISER), 12228–900 São José dos Campos – SP, Brazil
Shawn C. Shadden
Affiliation:
Department of Mechanical Engineering, University of California, Berkeley, CA 94720, USA
*
†Email address for correspondence: rempel@ita.br
Get access Rights & Permissions [Opens in a new window]

Abstract

Eulerian and Lagrangian tools are used to detect coherent structures in the velocity and magnetic fields of a mean-field dynamo, produced by direct numerical simulations of the three-dimensional compressible magnetohydrodynamic equations with an isotropic helical forcing and moderate Reynolds number. Two distinct stages of the dynamo are studied: the kinematic stage, where a seed magnetic field undergoes exponential growth; and the saturated regime. It is shown that the Lagrangian analysis detects structures with greater detail, in addition to providing information on the chaotic mixing properties of the flow and the magnetic fields. 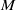The traditional way of detecting Lagrangian coherent structures using finite-time Lyapunov exponents is compared with a recently developed method called function $M$. The latter is shown to produce clearer pictures which readily permit the identification of hyperbolic regions in the magnetic field, where chaotic transport/dispersion of magnetic field lines is highly enhanced.

JFM classification

Mixing: Chaotic advection MHD and Electrohydrodynamics: Dynamo theory MHD and Electrohydrodynamics: MHD turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 729 , 25 August 2013 , pp. 309 - 329
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Archontis, V., Dorch, S. B. F. & Nordlund, A. 2003 Numerical simulations of kinematic dynamo action. Astron. Astrophys. 397, 393–399.Google Scholar
Baggaley, A. W., Barenghi, C. F., Shukurov, A. & Subramanian, K. 2009 Reconnecting flux-rope dynamo. Phys. Rev. E 80, 055301.Google Scholar
Beron-Vera, F. J., Olascoaga, M. J. & Goni, G. J. 2010 Surface ocean mixing inferred from different multisatellite altimetry measurements. J. Phys. Oceanogr. 40, 2466–2480.CrossRefGoogle Scholar
Blackman, E. G. 1996 Overcoming the backreaction on turbulent motions in the presence of magnetic fields. Phys. Rev. Lett. 77, 2694–2697.Google Scholar
Borgogno, D., Grasso, D., Pegoraro, F. & Schep, T. J. 2011 Barriers in the transition to global chaos in collisionless magnetic reconnection. I. Ridges on the finite time Lyapunov exponent field. Phys. Plasmas 18, 102307.CrossRefGoogle Scholar
Brandenburg, A. 2001 The inverse cascade and nonlinear alpha-effect in simulations of isotropic helical hydromagnetic turbulence. Astrophys. J. 550, 824–840.Google Scholar
Brandenburg, A., Jennings, R. L., Nordlund, A., Rieutord, M., Stein, R. F. & Tuominen, I. 1996 Magnetic structures in a dynamo simulation. J. Fluid Mech. 306, 325–352.Google Scholar
Brandenburg, A., Klapper, I. & Kurths, J. 1995 Generalized entropies in a turbulent dynamo simulation. Phys. Rev. E 52, R4602–R4605.Google Scholar
Brandenburg, A. & Subramanian, K. 2005 Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rep. 417, 1–209.Google Scholar
Branicki, M., Mancho, A. M. & Wiggins, S. 2011 A Lagrangian description of transport associated with a fronteddy interaction: application to data from the North-Western Mediterranean Sea. Physica D 240, 282–304.Google Scholar
Cattaneo, F., Hughes, D. W. & Kim, E.-J. 1996 Suppression of chaos in a simplified nonlinear dynamo model. Phys. Rev. Lett. 76, 2057–2060.Google Scholar
de la Cámara, A., Mancho, A. M., Ide, K., Serrano, E. & Mechoso, C. R. 2012 Routes of transport across the Antarctic polar vortex in the southern spring. J. Atmos. Sci. 69, 741–752.CrossRefGoogle Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.Google Scholar
Chertkov, M., Falkovich, G., Kolokolov, I. & Vergassola, M. 1999 Small-scale turbulent dynamo. Phys. Rev. Lett. 83, 4065–4068.Google Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids A 2, 765–777.Google Scholar
Chuychai, P., Ruffolo, D., Matthaeus, W. H. & Rowlands, G. 2005 Suppressed diffusive escape of topologically trapped magnetic field lines. Astrophys. J. 633, L49–L52.Google Scholar
Démoulin, P. 2006 Extending the concept of separatrices to QSLs for magnetic reconnection. Adv. Space Res. 37, 1269–1282.CrossRefGoogle Scholar
Donzis, D. A., Yeung, P. K. & Sreenivasan, K. R. 2008 Dissipation and enstrophy in isotropic turbulence: resolution effects and scaling in direct numerical simulations. Phys. Fluids 20, 045108.Google Scholar
Evans, T. E., Roeder, R. K. W., Carter, J. A. & Rapoport, B. I. 2004 Homoclinic tangles, bifurcations and edge stochasticity in diverted tokamaks. Contrib. Plasma Phys. 44, 235–240.CrossRefGoogle Scholar
Farazmand, M. & Haller, G. 2012 Computing Lagrangian coherent structures from their variational theory. Chaos 22, 013128.Google Scholar
Grasso, D., Borgogno, D., Pegoraro, F. & Schep, T. J. 2010 Barriers to eld line transport in 3D magnetic congurations. J. Phys.: Conf. Ser. 260, 012012.Google Scholar
Green, M. A., Rowley, C. W. & Haller, G. 2007 Detection of Lagrangian coherent structures in three-dimensional turbulence. J. Fluid Mech. 572, 111–120.Google Scholar
Haller, G. 2001 Distinguished material surfaces and coherent structures in three-dimensional fluid flows. Physica D 149, 248–277.Google Scholar
Haller, G. 2005 An objective definition of a vortex. J. Fluid Mech. 525, 1–26.Google Scholar
Haller, G. 2011 A variational theory of hyperbolic Lagrangian coherent structures. Physica D 240, 574–598.Google Scholar
Haller, G. & Beron-Vera, F. J. 2012 Geodesic theory of transport barriers in two-dimensional flows. Physica D 241, 1680–1702.Google Scholar
Haller, G. & Yuan, G. 2000 Lagrangian coherent structures and mixing in two-dimensional turbulence. Physica D 147, 352–370.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. Center for Turbulence Research Report CTR-S88, http://ctr.stanford.edu/Summer/201306111537.pdf.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Lawson, S. J. & Barakos, G. N. 2010 Computational fluid dynamics analyses of flow over weapons-bay geometries. J. Aircraft 47, 1605–1623.Google Scholar
Leoncini, X., Agullo, O., Muraglia, M. & Chandre, C. 2006 From chaos of lines to Lagrangian structures in flux conservative fields. Eur. Phys. J. B 53, 351–360.Google Scholar
Madrid, J. A. J. & Mancho, A. M. 2009 Distinguished trajectories in time dependent vector fields. Chaos 19, 013111.Google Scholar
Mendoza, C. & Mancho, A. M. 2010 Hidden geometry of ocean flows. Phys. Rev. Lett. 105, 038501.Google Scholar
Mendoza, C., Mancho, A. M. & Rio, M.-H. 2010 The turnstile mechanism across the Kuroshio current: analysis of dynamics in altimeter velocity fields. Nonlinear Process. Geophys. 17, 103–111.Google Scholar
Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Peacock, T. & Dabiri, J. 2010 Introduction to focus issue: Lagrangian coherent structures. Chaos 20, 017501.Google Scholar
Rempel, E. L., Chian, A. C.-L. & Brandenburg, A. 2011 Lagrangian coherent structures in nonlinear dynamos. Astrophys. J. Lett. 735, L9 (7pp).Google Scholar
Rempel, E. L., Chian, A.C.-L. & Brandenburg, A. 2012 Lagrangian chaos in an ABC-forced nonlinear dynamo. Phys. Scr. 86, 018405.CrossRefGoogle Scholar
Ruffolo, D., Matthaeus, W. H. & Chuychai, P. 2003 Trapping of solar energetic particles by the small-scale topology of solar wind turbulence. Astrophys. J. 597, L169–L172.Google Scholar
Santos, J. C., Büchner, J., Madjarska, M. S. & Alves, M. V. 2008 On the relation between DC current locations and an EUV bright point: a case study. Astron. Astrophys. 490, 345–352.CrossRefGoogle Scholar
Seripienlert, A., Ruffolo, D., Matthaeus, W. H. & Chuychai, P. 2010 Dropouts in solar energetic particles: associated with local trapping boundaries or current sheets? Astrophys. J. 711, 980–989.CrossRefGoogle Scholar
Servidio, S., Matthaeus, W. H., Shay, M. A., Dmitruk, P., Cassak, P. A. & Wan, M. 2010 Statistics of magnetic reconnection in two-dimensional magnetohydrodynamic turbulence. Phys. Plasmas 17, 032315.Google Scholar
Shadden, S. C. 2011 Lagrangian coherent structures. In Transport and Mixing in Laminar Flows, pp. 59–89. Wiley-VCH Verlag GmbH & Co. KGaA.CrossRefGoogle Scholar
Shadden, S. C., Lekien, F. & Marsden, J. E. 2005 Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Physica D 212, 271–304.Google Scholar
Varun, A. V., Balasubramanian, K. & Sujith, R. I. 2008 An automated vortex detection scheme using the wavelet transform of the d2 field. Exp. Fluids 45, 857–868.Google Scholar
Voth, G. A., Haller, G. & Gollub, J. P. 2002 Experimental measurements of stretching fields in fluid mixing. Phys. Rev. Lett. 88, 254501.Google Scholar
Weiss, J. 1991 The dynamics of enstrophy transfer in two-dimensional hydrodynamics. Physica D 48, 273–294.Google Scholar
Yeates, A. R. & Hornig, G. 2011 A generalized flux function for three-dimensional magnetic reconnection. Phys. Plasmas 18, 102118.Google Scholar
Yeates, A. R., Hornig, G. & Welsch, B. T. 2012 Lagrangian coherent structures in photospheric flows and their implications for coronal magnetic structures. Astron. Astrophys. 539, A1 (9pp).Google Scholar
Zel’dovich, Ya. B., Ruzmaikin, A. A., Molchanov, S. A. & Sokoloff, D. D. 1984 Kinematic dynamo problem in a linear velocity field. J. Fluid Mech. 144, 1–11.Google Scholar
Zhong, J., Huang, T. S. & Adrian, R. J. 1998 Extracting 3D vortices in turbulent fluid flow. IEEE Trans. Pattern Anal. Mach. Intell. 20, 193–199.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar
Zienicke, E., Politano, H. & Pouquet, A. 1998 Variable intensity of Lagrangian chaos in the nonlinear dynamo problem. Phys. Rev. Lett. 81, 4640–4643.Google Scholar