Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-26T17:44:46.457Z Has data issue: false hasContentIssue false
  • English
  • Français

Cessation and reversals of large-scale structures in square Rayleigh–Bénard cells

Published online by Cambridge University Press:  02 September 2019

Andrés Castillo-Castellanos Open the ORCID record for Andrés Castillo-Castellanos [Opens in a new window] ,
Anne Sergent Open the ORCID record for Anne Sergent [Opens in a new window] ,
Bérengère Podvin Open the ORCID record for Bérengère Podvin [Opens in a new window]  and
Maurice Rossi
Andrés Castillo-Castellanos
Affiliation:
CNRS, Sorbonne Université, Institut Jean Le Rond d’Alembert, F-75005 Paris, France CNRS, LIMSI, Université Paris-Saclay, F-91405 Orsay, France
Anne Sergent*
Affiliation:
CNRS, LIMSI, Université Paris-Saclay, F-91405 Orsay, France Sorbonne Université, UFR d’Ingénierie, F-75005 Paris, France
Bérengère Podvin
Affiliation:
CNRS, LIMSI, Université Paris-Saclay, F-91405 Orsay, France
Maurice Rossi
Affiliation:
CNRS, Sorbonne Université, Institut Jean Le Rond d’Alembert, F-75005 Paris, France
*
†Email address for correspondence: anne.sergent@limsi.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider direct numerical simulations of turbulent Rayleigh–Bénard convection inside two-dimensional square cells. For Rayleigh numbers 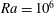$Ra=10^{6}$ to 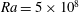$Ra=5\times 10^{8}$ and Prandtl numbers 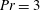$Pr=3$ and 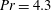$Pr=4.3$, two types of flow regimes are observed intermittently: consecutive flow reversals (CR), and extended cessations (EC). For each regime, we combine proper orthogonal decomposition (POD) and statistical tools on long-term data to characterise the dynamics of large-scale structures. For the CR regime, centrosymmetric modes are dominant and display a coherent dynamics, while non-centrosymmetric modes fluctuate randomly. For the EC regime, all POD modes follow Poissonian statistics and a non-centrosymmetric mode is dominant. To explore further the differences between the CR and EC regimes, an analysis based on a cluster partition of the POD phase space is proposed. This data-driven approach confirms the successive mechanisms of the generic reversal cycle in CR as proposed in Castillo-Castellanos et al. (J. Fluid Mech., vol. 808, 2016, pp. 614–640). However, these mechanisms may take one of multiple paths in the POD phase space. Inside the EC regime, this approach reveals the presence of two types of coherent time sequences (weak reversals and actual cessations) and more rarely intense plume crossings. Finally, we analyse within a range of Rayleigh numbers up to turbulent flow, the relation between dynamical regimes and the POD energetic contents as well as the residence time in each cluster.

JFM classification

Turbulent Flows: Turbulent convection Convection: Convection in cavities
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 877 , 25 October 2019 , pp. 922 - 954
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A. 1981 Conditional sampling in turbulence measurement. Annu. Rev. Fluid Mech. 13 (1), 131–156.10.1146/annurev.fl.13.010181.001023Google Scholar
Arthur, D. & Vassilvitskii, S. 2007 k-means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 1027–1035. Society for Industrial and Applied Mathematics.Google Scholar
Bai, K., Ji, D. & Brown, E. 2016 Ability of a low-dimensional model to predict geometry-dependent dynamics of large-scale coherent structures in turbulence. Phys. Rev. E 93 (2), 023117.Google Scholar
Bailon-Cuba, J., Emran, M. S. & Schumacher, J. 2010 Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 655, 152–173.10.1017/S0022112010000820Google Scholar
Bell, J. B., Colella, P. & Glaz, H. M. 1989 A second-order projection method for the incompressible Navier–Stokes equations. J. Comput. Phys. 283, 257–283.10.1016/0021-9991(89)90151-4Google Scholar
Brown, E. & Ahlers, G. 2006 Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 568, 351–386.10.1017/S0022112006002540Google Scholar
Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Reorientation of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084503.10.1103/PhysRevLett.95.084503Google Scholar
Castillo-Castellanos, A., Sergent, A. & Rossi, M. 2016 Reversal cycle in square Rayleigh–Bénard cells in turbulent regime. J. Fluid Mech. 808, 614–640.10.1017/jfm.2016.647Google Scholar
Chandra, M. & Verma, M. K. 2011 Dynamics and symmetries of flow reversals in turbulent convection. Phys. Rev. E 83 (6), 067303.Google Scholar
Chandra, M. & Verma, M. K. 2013 Flow reversals in turbulent convection via vortex reconnections. Phys. Rev. Lett. 110 (11), 114503.10.1103/PhysRevLett.110.114503Google Scholar
Das, A., Ghosal, U. & Kumar, K. 2000 Asymmetric squares as standing waves in Rayleigh–Bénard convection. Phys. Rev. E 62 (3), R3051.Google Scholar
Faranda, D., Podvin, B. & Sergent, A. 2019 On reversals in 2D turbulent Rayleigh–Bénard convection: insights from embedding theory and comparison with proper orthogonal decomposition analysis. Chaos 29, 033110.10.1063/1.5081031Google Scholar
Fauve, S., Herault, J., Michel, G. & Pétrélis, F. 2017 Instabilities on a turbulent background. J. Stat. Mech. 6, 064001.Google Scholar
Foroozani, N., Niemela, J. J., Armenio, V. & Sreenivasan, K. R. 2017 Reorientations of the large-scale flow in turbulent convection in a cube. Phys. Rev. E 95 (3), 033107.Google Scholar
Giannakis, D., Kolchinskaya, A., Krasnov, D. & Schumacher, J. 2018 Koopman analysis of the long-term evolution in a turbulent convection cell. J. Fluid Mech. 847, 735–767.10.1017/jfm.2018.297Google Scholar
Grossmann, S. & Lohse, D. 2003 On geometry effects in Rayleigh–Bénard convection. J. Fluid Mech. 486, 105–114.10.1017/S0022112003004270Google Scholar
Holmes, P., Lumley, J. L., Berkooz, G. & Rowley, C. W. 2012 Turbulence, Coherent Structures, Dynamical Systems and Symmetry, 2nd edn. Cambridge University Press.10.1017/CBO9780511919701Google Scholar
Horn, S. & Schmid, P. J. 2017 Prograde, retrograde, and oscillatory modes in rotating Rayleigh–Bénard convection. J. Fluid Mech. 831, 182–211.10.1017/jfm.2017.631Google Scholar
Hughes, G. O., Gayen, B. & Griffiths, R. W. 2013 Available potential energy in Rayleigh–Bénard convection. J. Fluid Mech. 729, R3.10.1017/jfm.2013.353Google Scholar
Hussain, A. K. M. F. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.10.1017/S0022112086001192Google Scholar
Jain, A. K. 2010 Data clustering: 50 years beyond k-means. Pattern Recognition Lett. 31 (8), 651–666.10.1016/j.patrec.2009.09.011Google Scholar
Kadanoff, L. P. 2001 Turbulent heat flow: structures and scaling. Phys. Today 54 (8), 34–39.10.1063/1.1404847Google Scholar
Kaiser, E., Noack, B. R., Cordier, L., Spohn, A., Segond, M., Abel, M., Daviller, G., Östh, J., Krajnovi, S. & Niven, R. K. 2014 Cluster-based reduced-order modelling of a mixing layer. J. Fluid Mech. 754, 365–414.10.1017/jfm.2014.355Google Scholar
Lhuillier, F., Hulot, G. & Gallet, Y. 2013 Statistical properties of reversals and chrons in numerical dynamos and implications for the geodynamo. Phys. Earth Planet. Inter. 220, 19–36.10.1016/j.pepi.2013.04.005Google Scholar
Lumley, J. L. 1967 The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Wave Propagation (ed. Yaglom, A. M. & Tatarski, V. I.), pp. 166–178. Nauka.Google Scholar
McFadden, P. L. & Merrill, R. T. 1986 Geodynamo energy source constraints from palaeomagnetic data. Phys. Earth Planet. Inter. 43 (1), 22–33.10.1016/0031-9201(86)90118-4Google Scholar
Merrill, R., McElhinny, M. & McFadden, P. 1998 Chapter five reversals of the earth’s magnetic field. In The Magnetic Field of the Earth: Paleomagnetism, the Core, and the Deep Mantle, International Geophysics, vol. 63, pp. 163–215. Academic Press.Google Scholar
Molenaar, D., Clercx, H. J. H. & Van Heijst, G. J. F. 2004 Angular momentum of forced 2D turbulence in a square no-slip domain. Physica D 196, 329–340.10.1016/j.physd.2004.06.001Google Scholar
Ni, R., Huang, S.-D. & Xia, K.-Q. 2015 Reversals of the large-scale circulation in quasi-2D Rayleigh–Bénard convection. J. Fluid Mech. 778, R5.10.1017/jfm.2015.433Google Scholar
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2001 The wind in confined thermal convection. J. Fluid Mech. 449, 169–178.10.1017/S0022112001006310Google Scholar
Okabe, A., Boots, B., Sugihara, K. & Chiu, S. N. 2009 Spatial Tessellations: Concepts and Applications of Voronoi Diagrams, vol. 501. John Wiley & Sons.Google Scholar
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V. et al. 2011 Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830.Google Scholar
Petschel, K., Wilczek, M., Breuer, M., Friedrich, R. & Hansen, U. 2011 Statistical analysis of global wind dynamics in vigorous Rayleigh–Bénard convection. Phys. Rev. E 84 (2), 026309.Google Scholar
Podvin, B. & Sergent, A. 2015 A large-scale investigation of wind reversal in a square Rayleigh–Bénard cell. J. Fluid Mech. 766, 172–201.10.1017/jfm.2015.15Google Scholar
Podvin, B. & Sergent, A. 2017 Precursor for wind reversal in a square Rayleigh–Bénard cell. Phys. Rev. E 95 (1), 013112.Google Scholar
van der Poel, E. P., Stevens, R. J. A. M. & Lohse, D. 2011 Connecting flow structures and heat flux in turbulent Rayleigh–Bénard convection. Phys. Rev. E 84 (4), 045303.Google Scholar
Popinet, S. 2003 Gerris: a tree-based adaptive solver for the incompressible euler equations in complex geometries. J. Comput. Phys. 190 (2), 572–600.10.1016/S0021-9991(03)00298-5Google Scholar
Popinet, S. 2009 An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 228 (16), 5838–5866.10.1016/j.jcp.2009.04.042Google Scholar
Popinet, S. 2015 A quadtree-adaptive multigrid solver for the Serre–Green–Naghdi equations. J. Comput. Phys. 302, 336–358.10.1016/j.jcp.2015.09.009Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.10.1017/S0022112010001217Google Scholar
Shraiman, B. I. & Siggia, E. D. 1990 Heat transport in high-Rayleigh-number convection. Phys. Rev. A 42 (6), 3650–3653.10.1103/PhysRevA.42.3650Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures part I: coherent structures. Q. Appl. Maths 45 (3), 561–571.10.1090/qam/910462Google Scholar
Sreenivasan, K. R., Bershadskii, A. & Niemela, J. J. 2002 Mean wind and its reversal in thermal convection. Phys. Rev. E 65 (5), 056306.Google Scholar
Sugiyama, K., Ni, R., Stevens, R. J. A. M., Chan, T. S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105 (3), 034503.10.1103/PhysRevLett.105.034503Google Scholar
Valet, J.-P., Fournier, A., Courtillot, V. & Herrero-Bervera, E. 2012 Dynamical similarity of geomagnetic field reversals. Nature 490 (7418), 89–93.10.1038/nature11491Google Scholar
Van Heijst, G. J. F., Clercx, H. J. H. & Molenaar, D. 2006 The effects of solid boundaries on confined two-dimensional turbulence. J. Fluid Mech. 554, 411–431.10.1017/S002211200600886XGoogle Scholar
Vasilev, A. Y. & Frick, P. G. 2011 Reversals of large-scale circulation in turbulent convection in rectangular cavities. JETP Lett. 93 (6), 330–334.10.1134/S0021364011060117Google Scholar
Wicht, J., Stellmach, S. & Harder, H. 2009 Numerical Models of the Geodynamo: From Fundamental Cartesian Models to 3D Simulations of Field Reversals. pp. 107–158. Springer.Google Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.10.1017/S002211209500125XGoogle Scholar
Xi, H.-D. & Xia, K.-Q. 2007 Cessations and reversals of the large-scale circulation in turbulent thermal convection. Phys. Rev. E 75 (6), 066307.Google Scholar
Xi, H.-D. & Xia, K.-Q. 2008a Azimuthal motion, reorientation, cessation, and reversal of the large-scale circulation in turbulent thermal convection: a comparative study in aspect ratio one and one-half geometries. Phys. Rev. E 78 (3), 036326.Google Scholar
Xi, H.-D. & Xia, K.-Q. 2008b Flow mode transitions in turbulent thermal convection. Phys. Fluids 20 (5), 055104.10.1063/1.2920444Google Scholar
Xi, H.-D., Zhou, Q. & Xia, K.-Q. 2006 Azimuthal motion of the mean wind in turbulent thermal convection. Phys. Rev. E 73 (5), 056312.Google Scholar
Zhang, X. & Zikanov, O. 2015 Two-dimensional turbulent convection in a toroidal duct of a liquid metal blanket of a fusion reactor. J. Fluid Mech. 779, 36–52.10.1017/jfm.2015.421Google Scholar