Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-25T13:52:55.119Z Has data issue: false hasContentIssue false
  • English
  • Français

Capturing nonlinear dynamics of two-fluid Couette flows with asymptotic models

Published online by Cambridge University Press:  13 October 2016

A. Kalogirou ,
R. Cîmpeanu ,
E. E. Keaveny  and
D. T. Papageorgiou
A. Kalogirou
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK School of Mathematics, University of Leeds, Leeds LS9 2JT, UK
R. Cîmpeanu
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
E. E. Keaveny
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
D. T. Papageorgiou*
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
*
†Email address for correspondence: d.papageorgiou@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The nonlinear stability of two-fluid Couette flows is studied using a novel evolution equation whose dynamics is validated by direct numerical simulation (DNS). The evolution equation incorporates inertial effects at arbitrary Reynolds numbers through a non-local term arising from the coupling between the two fluid regions, and is valid when one of the layers is thin. The equation predicts asymmetric solutions and exhibits bistability, features that are essential observations in the experiments of Barthelet et al. (J. Fluid Mech., vol. 303, 1995, pp. 23–53). Related low-inertia models have been used in qualitative predictions rather than the direct comparisons carried out here, and ad hoc modifications appear to be necessary in order to predict asymmetry and bistability. Comparisons between model solutions and DNS show excellent agreement at Reynolds numbers of 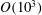$O(10^{3})$ found in the experiments. Direct comparisons are also made with the available experimental results of Barthelet et al. (J. Fluid Mech., vol. 303, 1995, pp. 23–53) when the thin layer occupies 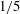$1/5$ of the channel height. Pointwise comparisons of the travelling wave shapes are carried out, and once again the agreement is very good.

JFM classification

Instability: Nonlinear instability Interfacial Flows (free surface): Thin films
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 806 , 10 November 2016 , R1
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akrivis, G., Papageorgiou, D. T. & Smyrlis, Y.-S. 2012 Computational study of the dispersively modified Kuramoto–Sivashinsky equation. SIAM J. Sci. Comput. 34, A792–A813.Google Scholar
Barthelet, P. & Charru, F. 1995 Interfacial long waves in two-layer shear flows: model equations in the light of experiments. In Advances Multi-fluid flows: Proceedings of the Conference on Multi-Fluid Flows and Interfacial Instabilities (ed. Renardy, Y. Y., Coward, A. V., Papageorgiou, D. T. & Sun, S.-M.), pp. 13–32. SIAM.Google Scholar
Barthelet, P., Charru, F. & Fabre, J. 1995 Experimental study of interfacial long waves in a two-layer shear flow. J. Fluid Mech. 303, 23–53.Google Scholar
Charru, F. & Fabre, J. 1994 Long waves at the interface between two viscous fluids. Phys. Fluids 6 (3), 1223–1235.Google Scholar
Craster, R. V. & Matar, O. K. 2009 Dynamics and stability of thin liquid films. Rev. Mod. Phys. 81, 1131–1198.Google Scholar
Fowler, A. 2011 Mathematical Geoscience. Springer.Google Scholar
Hooper, A. P. 1985 Long-wave instability at the interface between two viscous fluids: thinlayer effects. Phys. Fluids 28, 1613–1618.Google Scholar
Hooper, A. P. & Boyd, W. G. C. 1983 Shear-flow instability at the interface between two viscous fluids. J. Fluid Mech. 128, 507–528.Google Scholar
Hooper, A. P. & Grimshaw, R. 1985 Nonlinear instability at the interface between two viscous fluids. Phys. Fluids 28, 37–45.Google Scholar
Hooper, A. P. & Grimshaw, R. 1988 Travelling wave solutions to the Kuramoto–Sivashinsky equation. Wave Motion 10, 405–420.CrossRefGoogle Scholar
Kalogirou, A.2014 Nonlinear dynamics of surfactant-laden multilayer shear flows and related systems. PhD thesis, Imperial College, London.Google Scholar
Kalogirou, A. & Papageorgiou, D. T. 2016 Nonlinear dynamics of surfactant-laden two-fluid Couette flows in the presence of inertia. J. Fluid Mech. 802, 5–36.Google Scholar
Papageorgiou, D. T., Maldarelli, C. & Rumschitzki, D. S. 1990 Nonlinear interfacial stability of core–annular film flows. Phys. Fluids A 2 (3), 340–352.Google Scholar
Popinet, S. 2003 Gerris: a tree-based adaptive solver for the incompressible Euler equations in complex geometries. J. Comput. Phys. 190, 572–600.Google Scholar
Renardy, Y. Y. 1985 Instability at the interface between two shearing fluids in a channel. Phys. Fluids 28, 3441–3443.Google Scholar
Renardy, Y. Y. 1987 The thin-layer effect and interfacial stability in a two-layer Couette flow with similar liquids. Phys. Fluids 30, 1627–1637.CrossRefGoogle Scholar
Tseluiko, D. & Kalliadasis, S. 2011 Nonlinear waves in counter-current gas–liquid film flow. J. Fluid Mech. 673, 19–59.Google Scholar
Tseluiko, D. & Papageorgiou, D. T. 2010 Dynamics of an electrostatically modified Kuramoto–Sivashinsky–Korteweg–de Vries equation arising in falling film flows. Phys. Rev. E 82, 016322, 1–12.Google Scholar
Yih, C.-S. 1967 Instability due to viscosity stratification. J. Fluid Mech. 27, 337–352.CrossRefGoogle Scholar