Article contents
Bifurcation analysis of the primary instability in the flow around a flexibly mounted circular cylinder
Published online by Cambridge University Press: 08 October 2019
Abstract
The nonlinear character of the primary bifurcation is investigated for the flow around a flexibly mounted circular cylinder. We have considered the cases in which the cylinder can oscillate in the transverse direction only and in both transverse and in-line directions. Low and high values of mass ratio (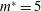 $m^{\ast }=5$ and 50) were studied, and reduced velocity (
$m^{\ast }=5$ and 50) were studied, and reduced velocity ( $V_{r}$) values are chosen inside (
$V_{r}$) values are chosen inside (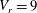 $V_{r}=9$) and outside (
$V_{r}=9$) and outside (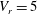 $V_{r}=5$ and
$V_{r}=5$ and 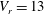 $V_{r}=13$) the lock-in range for low Reynolds numbers. For each combination of
$V_{r}=13$) the lock-in range for low Reynolds numbers. For each combination of 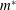 $m^{\ast }$ and
$m^{\ast }$ and 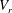 $V_{r}$, a global linear stability analysis was applied to find the critical Reynolds number
$V_{r}$, a global linear stability analysis was applied to find the critical Reynolds number 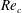 $Re_{c}$ of the fluid–structure system. For
$Re_{c}$ of the fluid–structure system. For 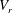 $V_{r}$ in the lock-in range, the values of
$V_{r}$ in the lock-in range, the values of 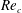 $Re_{c}$ were noticeably less than the critical Reynolds number of the flow around a fixed circular cylinder (
$Re_{c}$ were noticeably less than the critical Reynolds number of the flow around a fixed circular cylinder (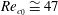 $Re_{c_{0}}\cong 47$). On the other hand, for
$Re_{c_{0}}\cong 47$). On the other hand, for 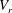 $V_{r}$ outside the lock-in range, the values of
$V_{r}$ outside the lock-in range, the values of 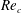 $Re_{c}$ were close to
$Re_{c}$ were close to 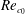 $Re_{c_{0}}$. Next, nonlinear analyses were performed in the vicinity of
$Re_{c_{0}}$. Next, nonlinear analyses were performed in the vicinity of 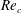 $Re_{c}$ for each case. Subcritical character (with hysteresis) was observed for
$Re_{c}$ for each case. Subcritical character (with hysteresis) was observed for 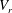 $V_{r}$ in the lock-in range, while for
$V_{r}$ in the lock-in range, while for 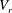 $V_{r}$ outside the lock-in region the bifurcations were found to be supercritical (without hysteresis). This shows that when the coupling between the structure and flow is strong, due to the proximity of the natural frequencies of the isolated systems, it significantly changes both the linear and nonlinear responses observed.
$V_{r}$ outside the lock-in region the bifurcations were found to be supercritical (without hysteresis). This shows that when the coupling between the structure and flow is strong, due to the proximity of the natural frequencies of the isolated systems, it significantly changes both the linear and nonlinear responses observed.
JFM classification
- Type
- JFM Rapids
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 14
- Cited by




