Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-05-25T09:54:22.332Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic adjoint solutions for the 2-D incompressible Euler equations using the Green's function approach

Published online by Cambridge University Press:  13 June 2022

Carlos Lozano Open the ORCID record for Carlos Lozano [Opens in a new window]  and
Jorge Ponsin
Carlos Lozano
Affiliation:
Computational Aerodynamics, National Institute of Aerospace Technology (INTA), Carretera de Ajalvir, Km 4, 28850 Torrejon de Ardoz, Spain
Jorge Ponsin*
Affiliation:
Computational Aerodynamics, National Institute of Aerospace Technology (INTA), Carretera de Ajalvir, Km 4, 28850 Torrejon de Ardoz, Spain
*
† Email address for correspondence: lozanorc@inta.es
Get access Rights & Permissions [Opens in a new window]

Abstract

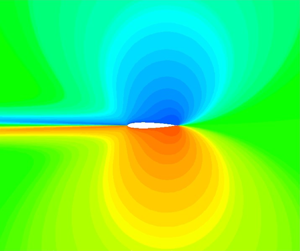
The Green's function approach of Giles and Pierce (J. Fluid Mech., vol. 426, 2001, pp. 327–345) is used to build the lift and drag based analytic adjoint solutions for the two-dimensional incompressible Euler equations around irrotational base flows. The drag-based adjoint solution turns out to have a very simple closed form in terms of the flow variables and is smooth throughout the flow domain, while the lift-based solution is singular at rear stagnation points and sharp trailing edges owing to the Kutta condition. This singularity is propagated to the whole dividing streamline (which includes the incoming stagnation streamline and the wall) upstream of the rear singularity (trailing edge or rear stagnation point) by the sensitivity of the Kutta condition to changes in the stagnation pressure.

JFM classification

Aerodynamics: Aerodynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 943 , 25 July 2022 , A22
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, W.K. & Venkatakrishnan, V. 1999 Aerodynamic design optimization on unstructured grids with a continuous adjoint formulation. Comput. Fluids 28, 443–480.CrossRefGoogle Scholar
Baeza, A., Castro, C., Palacios, F. & Zuazua, E. 2009 2-D Euler shape design on nonregular flows using adjoint Rankine-Hugoniot relations. AIAA J. 47 (3), 552–562.CrossRefGoogle Scholar
Castro, C., Lozano, C., Palacios, F. & Zuazua, E. September 2007 Systematic continuous adjoint approach to viscous aerodynamic design on unstructured grids. AIAA J. 45 (9), 2125–2139.CrossRefGoogle Scholar
Chadwick, E., Christian, J.M., Kapoulas, A. & Chalasani, K. 2019 The theory and application of Eulerlets. Phys. Fluids 31, 047106.CrossRefGoogle Scholar
Delfour, M.C. & Zolésio, J.-P. 2011 Shape and Geometries: Analysis, Differential Calculus and Optimization, 2nd edn. SIAM.CrossRefGoogle Scholar
Emanuel, G. 2000 Analytical Fluid Dynamics, 2nd edn (chapter 5.7). CRC Press.CrossRefGoogle Scholar
Fidkowski, K. & Darmofal, D. 2011 Review of output-based error estimation and mesh adaptation in computational fluid dynamics. AIAA J. 49 (4), 673–694.CrossRefGoogle Scholar
Fidkowski, K.J. & Roe, P.L. 2010 An entropy adjoint approach to mesh refinement. SIAM J. Sci. Comput. 32 (3), 1261–1287.CrossRefGoogle Scholar
Giles, M.B., Duta, M.C., Müller, J.-D. & Pierce, N.A. 2003 Algorithm developments for discrete adjoint methods. AIAA J. 41 (2), 198–205.CrossRefGoogle Scholar
Giles, M. & Haimes, R. 1990 Advanced interactive visualization for CFD. Comput. Syst. Engng 1 (1), 51–62.CrossRefGoogle Scholar
Giles, M.B. & Pierce, N.A. 1997 Adjoint equations in CFD: duality, boundary conditions and solution behavior. AIAA Paper 97-1850.Google Scholar
Giles, M.B. & Pierce, N.A. 1998 On the properties of solutions of the adjoint Euler equations. In Numerical Methods for Fluid Dynamics VI (ed. M. Baines). ICFD.Google Scholar
Giles, M. & Pierce, N. 1999 Improved lift and drag estimates using adjoint Euler equations. AIAA Paper 99-3293.CrossRefGoogle Scholar
Giles, M. & Pierce, N. 2000 An introduction to the adjoint approach to design. Flow Turbul. Combust. 65 (3), 393–415.CrossRefGoogle Scholar
Giles, M.B. & Pierce, N.A. 2001 Analytic adjoint solutions for the quasi-one-dimensional Euler equations. J. Fluid Mech. 426, 327–345.CrossRefGoogle Scholar
Giles, M.B. & Pierce, N.A. 2002 Adjoint error correction for integral outputs. In Error Estimation and Solution Adaptive Discretization in Computational Fluid Dynamics (ed. T. Barth & H. Deconinck), Lecture Notes in Computer Science and Engineering, vol. 25, pp. 47–95. Springer Verlag.CrossRefGoogle Scholar
Jameson, A. 1988 Aerodynamic design via control theory. J. Sci. Comput. 3 (3), 233–260.CrossRefGoogle Scholar
Katz, J. & Plotkin, A. 2001 Low Speed Aerodynamics, 2nd edn. Cambridge University Press.CrossRefGoogle Scholar
Kavvadias, I., Papoutsis-Kiachagias, E. & Giannakoglou, K. 2015 On the proper treatment of grid sensitivities in continuous adjoint methods for shape optimization. J. Comput. Phys. 301, 1–18.CrossRefGoogle Scholar
Kenway, G.K., Mader, C.A., He, P. & Martins, J.R. 2019 Effective adjoint approaches for computational fluid dynamics. Prog. Aerosp. Sci. 110, 100542.CrossRefGoogle Scholar
Kroger, J., Kuhl, N. & Rung, T. 2018 Adjoint volume-of-fluid approaches for the hydrodynamic optimisation of ships. Ship Technol. Res. 65 (1), 47–68.CrossRefGoogle Scholar
Kühl, N., Müller, P. & Rung, T. 2021 Continuous adjoint complement to the Blasius equation. Phys. Fluids 33 (3), 033608.CrossRefGoogle Scholar
Lozano, C. 2012 Discrete surprises in the computation of sensitivities from boundary integrals in the continuous adjoint approach to inviscid aerodynamic shape optimization. Comput. Fluids 56, 118–127.CrossRefGoogle Scholar
Lozano, C. 2017 On mesh sensitivities and boundary formulas for discrete adjoint-based gradients in inviscid aerodynamic shape optimization. J. Comput. Phys. 346, 403–436.CrossRefGoogle Scholar
Lozano, C. 2018 Singular and discontinuous solutions of the adjoint Euler equations. AIAA J. 56 (11), 4437–4452.CrossRefGoogle Scholar
Lozano, C. 2019 a Entropy and adjoint methods. J. Sci. Comput. 81, 2447–2483.CrossRefGoogle Scholar
Lozano, C. 2019 b Watch your adjoints! Lack of mesh convergence in inviscid adjoint solutions. AIAA J. 57 (9), 3991–4006.CrossRefGoogle Scholar
Lozano, C. & Ponsin, J. 2012 Remarks on the numerical solution of the adjoint quasi-one-dimensional Euler equations. Intl J. Numer. Meth. Fluids 69 (5), 966–982.CrossRefGoogle Scholar
Lozano, C. & Ponsin, J. 2021 a Exact inviscid drag-adjoint solution for subcritical flows. AIAA J. 59 (12), 5369–5373.CrossRefGoogle Scholar
Lozano, C. & Ponsin, J. 2021 b On the mesh divergence of inviscid adjoint solutions. WCCM-ECCOMAS2020 (ed. F. Chinesta, R. Abgrall, O. Allix & M. Kaliske). Scipedia. doi:10.23967/wccm-eccomas.2020.258.CrossRefGoogle Scholar
Lozano, C. & Ponsin, J. 2022 Singularity and mesh divergence of inviscid adjoint solutions at solid walls. arXiv:2201.08129.CrossRefGoogle Scholar
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46, 493–517.CrossRefGoogle Scholar
Marta, A.C., Shankaran, S., Wang, Q. & Venugopal, P. 2013 Interpretation of adjoint solutions for turbomachinery flows. AIAA J. 51 (7), 1733–1744.CrossRefGoogle Scholar
Milne-Thomson, L.M. 1962 Theoretical Hydrodymanics, 4th edn. Macmillan.Google Scholar
Nadarajah, S. & Jameson, A. 2000 A comparison of the continuous and discrete adjoint approach to automatic aerodynamic optimization. AIAA Paper 2000-0667.CrossRefGoogle Scholar
Othmer, C. 2014 Adjoint methods for car aerodynamics. J. Math. Indus. 4 (1), 6.CrossRefGoogle Scholar
Peter, J. & Dwight, R.P. 2010 Numerical sensitivity analysis for aerodynamic optimization: a survey of approaches. Comput. Fluids 39 (10), 373–391.CrossRefGoogle Scholar
Peter, J., Renac, F. & Labbé, C. 2022 Analysis of finite-volume discrete adjoint fields for two-dimensional compressible Euler flows. J. Comput. Phys. 449, 110811.CrossRefGoogle Scholar
Venditti, D.A. & Darmofal, D.L. 2002 Grid adaptation for functional outputs: application to two-dimensional inviscid flows. J. Comput. Phys. 176, 40–69.CrossRefGoogle Scholar