Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-26T13:23:48.869Z Has data issue: false hasContentIssue false
  • English
  • Français

Analysis of the two-dimensional dynamics of a Mach 1.6 shock wave/transitional boundary layer interaction using a RANS based resolvent approach

Published online by Cambridge University Press:  16 January 2019

N. Bonne Open the ORCID record for N. Bonne [Opens in a new window] ,
V. Brion ,
E. Garnier ,
R. Bur ,
P. Molton ,
D. Sipp  and
L. Jacquin
N. Bonne*
Affiliation:
ONERA-DAAA, 8 rue des Vertugadins, 92190 Meudon, France
V. Brion
Affiliation:
ONERA-DAAA, 8 rue des Vertugadins, 92190 Meudon, France
E. Garnier
Affiliation:
ONERA-DAAA, 8 rue des Vertugadins, 92190 Meudon, France
R. Bur
Affiliation:
ONERA-DAAA, 8 rue des Vertugadins, 92190 Meudon, France
P. Molton
Affiliation:
ONERA-DAAA, 8 rue des Vertugadins, 92190 Meudon, France
D. Sipp
Affiliation:
ONERA-DAAA, 8 rue des Vertugadins, 92190 Meudon, France
L. Jacquin
Affiliation:
ONERA-MFE, Chemin de la Hunire – BP 80100, 91123 Palaiseau CEDEX, France
*
†Email address for correspondence: nicolas.bonne@onera.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

A two-dimensional analysis of the resolvent spectrum of a Mach 1.6 transitional boundary layer impacted by an oblique shock wave is carried out. The investigation is based on a two-dimensional mean flow obtained by a RANS model that includes a transition criterion. The goal is to evaluate whether such a low cost RANS based resolvent approach is capable of describing the frequencies and physics involved in this transitional boundary layer/shock-wave interaction. Data from an experiment and a companion large eddy simulation (LES) are utilized as reference for the validation of the method. The flow is characterized by a laminar boundary layer upstream, a laminar separation bubble (LSB) in the interaction region and a turbulent boundary layer downstream. The flow exhibits low amplitude unsteadiness in the LSB and at the reflected shock wave with three particular oscillation frequencies, qualified as low, medium and high in reference to their range in Strouhal number, here based on free stream velocity and LSB length (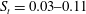$S_{t}=0.03{-}0.11$, 0.3–0.4 and 2–3 respectively). Through the resolvent analysis this dynamics is found to correspond to an amplifier behaviour of the flow. The resolvent responses match the averaged Fourier mode of the time dependent flow field, here described by the LES, with a close agreement in frequency and spatial distribution, thereby validating the resolvent approach. The low frequency dynamics relates to a pseudo-resonance process that sequentially implies the amplification in the separated shear layer of the LSB, an excitation of the shock foot and a backward travelling density wave. As this wave hits back the separation point the amplification in the shear layer starts again and loops. The medium and high frequency modes relate to the periodic expansion/reduction of the bubble and to the turbulent fluctuations at the reattachment point of the bubble, respectively.

JFM classification

Boundary Layers: Boundary layer separation Compressible Flows: Shock waves Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 862 , 10 March 2019 , pp. 1166 - 1202
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abu-Ghannam, B. J. & Shaw, R. 1980 Natural transition of boundary layers the effects of turbulence, pressure gradient, and flow history. J. Mech. Engng Sci. 22 (5), 213–228.Google Scholar
Agostini, L., Larchevêque, L. & Dupont, P. 2015 Mechanism of shock unsteadiness in separated shock/boundary–layer interactions. Phys. Fluids 27 (12), 126103.Google Scholar
Agostini, L., Larchevêque, L., Dupont, P., Debiève, J.-F. & Dussauge, J.-P. 2012 Zones of influence and shock motion in a shock/boundary-layer interaction. AIAA J. 50 (6), 1377–1387.Google Scholar
Alam, M. & Sandham, N. D. 2000 Direct numerical simulation of short laminar separation bubbles with turbulent reattachment. J. Fluid Mech. 403, 223–250.Google Scholar
Arnal, D. 1984 Special course on stability and transition of laminar flow. In AGARD Special Course at the von K.rm.n Institute, AGARD Report No 709, pp. 26–30.Google Scholar
Arnal, D., Houdeville, R., Séraudie, A. & Vermeersch, O. 2011 Overview of laminar-turbulent transition investigations at Onera Toulouse. In 41st AIAA Fluid Dynamics Conference and Exhibit, p. 3074. AIAA.Google Scholar
Babinsky, H. & Harvey, J. K. 2011 Shock Wave-Boundary-Layer Interactions, vol. 32. Cambridge University Press.Google Scholar
Beneddine, S., Sipp, D., Arnault, A., Dandois, J. & Lesshafft, L. 2016 Conditions for validity of mean flow stability analysis. J. Fluid Mech. 798, 485–504.Google Scholar
Boris, J. P., Grinstein, F. F., Oran, E. S. & Kolbe, R. L. 1992 New insights into large eddy simulation. Fluid Dyn. Res. 10 (4–6), 199–228.Google Scholar
Borodulin, V. I., Kachanov, Y. S. & Roschektayev, A. P. 2011 Experimental detection of deterministic turbulence. J. Turbul. (12), N23.Google Scholar
Brandt, L., Sipp, D., Pralits, J. O. & Marquet, O. 2011 Effect of base-flow variation in noise amplifiers: the flat-plate boundary layer. J. Fluid Mech. 687, 503–528.Google Scholar
Bur, R. & Garnier, E. 2016 Transition effect on a shock-wave/boundary layer interaction. In The CAero2 Platform: Dissemination of Computational Case Studies in Aeronautics, ECCOMAS Congress 2016, Crete Island (Greece), June 5–10, 2016. AIAA.Google Scholar
Casalis, G. & Arnal, D.1996 Elfin ii subtask 3: Database method–development and validation of the simplified method for pure crossflow instability at low speed. ELFIN II-European Laminar Flow Investigation. Tech. Rep. (145).Google Scholar
Chang, C.-L. & Malik, M. R. 1994 Oblique-mode breakdown and secondary instability in supersonic boundary layers. J. Fluid Mech. 273, 323–360.Google Scholar
Clemens, N. T. & Narayanaswamy, V. 2014 Low-frequency unsteadiness of shock wave/turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 46, 469–492.Google Scholar
Cliquet, J., Houdeville, R. & Arnal, D. 2008 Application of laminar-turbulent transition criteria in Navier–Stokes computations. AIAA J. 46 (5), 1182–1190.Google Scholar
Crouch, J. D., Garbaruk, A., Magidov, D. & Travin, A. 2009 Origin of transonic buffet on aerofoils. J. Fluid Mech. 628, 357–369.Google Scholar
Délery, J., Marvin, J. G. & Reshotko, E.1986 Shock-wave boundary layer interactions. Tech. Rep. DTIC Document.Google Scholar
Dolling, D. S. 2001 Fifty years of shock-wave/boundary-layer interaction research: What next? AIAA J. 39 (8), 1517–1531.Google Scholar
Dumoulin, A.2004 Validation de modeles de transition dans le code Navier–Stokes elsa. Rapport de stage ONERA.Google Scholar
Dupont, P., Haddad, C. & Debiève, J. F. 2006 Space and time organization in a shock-induced separated boundary layer. J. Fluid Mech. 559, 255–277.Google Scholar
Dussauge, J.-P., Dupont, P. & Debiève, J.-F. 2006 Unsteadiness in shock wave boundary layer interactions with separation. Aerosp. Sci. Technol. 10 (2), 85–91.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1993 Stochastic forcing of the linearized Navier–Stokes equations. Phys. Fluids A 5 (11), 2600–2609.Google Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2007 Effects of upstream boundary layer on the unsteadiness of shock-induced separation. J. Fluid Mech. 585, 369–394.Google Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2009 Low-frequency dynamics of shock-induced separation in a compression ramp interaction. J. Fluid Mech. 636, 397–425.Google Scholar
Garnier, E., Adams, N. & Sagaut, P. 2009 Large Eddy Simulation for Compressible Flows. Springer Science & Business Media.Google Scholar
Gleyzes, C., Cousteix, J. & Bonnet, J. L. 1985 Theoretical and experimental study of low reynolds number transitional separation bubbles. In Conference on Low Reynolds Number Airfoil Aerodynamics, Notre Dame, IN, pp. 137–152. AIAA.Google Scholar
Grilli, M., Schmid, P. J., Hickel, S. & Adams, N. A. 2012 Analysis of unsteady behaviour in shockwave turbulent boundary layer interaction. J. Fluid Mech. 700, 16–28.Google Scholar
Langtry, R. B.2006 A correlation-based transition model using local variables for unstructured parallelized CFD codes. PhD thesis, Universität Stuttgart.Google Scholar
Larchevêque, L. 2016 Low- and medium-frequency unsteadinesses in a transitional shock–boundary reflection with separation. In 54th AIAA Aerospace Sciences Meeting, p. 1833. AIAA.Google Scholar
Mack, L. M.1984 Boundary-layer linear stability theory. Tech. Rep. DTIC Document.Google Scholar
Marxen, O., Lang, M., Rist, U. & Wagner, S. 2003 A combined experimental/numerical study of unsteady phenomena in a laminar separation bubble. Flow Turbul. Combust. 71 (1–4), 133–146.Google Scholar
Marxen, O., Rist, U. & Wagner, S. 2004 Effect of spanwise-modulated disturbances on transition in a separated boundary layer. AIAA J. 42 (5), 937–944.Google Scholar
Mary, I., Sagaut, P. & Deville, M. 2000 An algorithm for unsteady viscous flows at all speeds. Intl J. Numer. Methods Fluids 34 (5), 371–401.Google Scholar
Mettot, C.2013 Stabilité linéaire, sensibilité et contrôle passif d’écoulements turbulents par différences finies. PhD thesis, Ecole Polytechnique X.Google Scholar
Nichols, J. W., Larsson, J., Bernardini, M. & Pirozzoli, S. 2017 Stability and modal analysis of shock/boundary layer interactions. Theor. Comput. Fluid Dyn. 31 (1), 33–50.Google Scholar
Pagella, A., Babucke, A. & Rist, U. 2004 Two-dimensional numerical investigations of small-amplitude disturbances in a boundary layer at ma = 4. 8: compression corner versus impinging shock wave. Phys. Fluids 16 (7), 2272–2281.Google Scholar
Pagella, A., Rist, U. & Wagner, S. 2002 Numerical investigations of small-amplitude disturbances in a boundary layer with impinging shock wave at ma = 4. 8. Phys. Fluids 14 (7), 2088–2101.Google Scholar
Piponniau, S., Dussauge, J. P., Debieve, J. F. & Dupont, P. 2009 A simple model for low-frequency unsteadiness in shock-induced separation. J. Fluid Mech. 629, 87–108.Google Scholar
Pirozzoli, S. & Grasso, F. 2006 Direct numerical simulation of impinging shock wave/turbulent boundary layer interaction at m = 2. 25. Phys. Fluids 18 (6), 065113.Google Scholar
Rist, U. 2003 Instability and transition mechanisms in laminar separation bubbles. Low Reynolds Number Aerodynamics on Aircraft Including Applications in Emerging UAV Technology.Google Scholar
Robinet, J-Ch. 2007 Bifurcations in shock-wave/laminar-boundary–layer interaction: global instability approach. J. Fluid Mech. 579, 85–112.Google Scholar
Samimy, M., Arnette, S. A. & Elliott, G. S. 1994 Streamwise structures in a turbulent supersonic boundary layer. Phys. Fluids 6 (3), 1081–1083.Google Scholar
Sansica, A., Sandham, N. D. & Hu, Z. 2014 Forced response of a laminar shock-induced separation bubble. Phys. Fluids 26 (9), 093601.Google Scholar
Sansica, A., Sandham, N. D. & Hu, Z. 2016 Instability and low-frequency unsteadiness in a shock-induced laminar separation bubble. J. Fluid Mech. 798, 5–26.Google Scholar
Sartor, F.2014 Instationnarités dans les interactions choc/couche-limite en régime transsonique: étude expérimentale et analyse de stabilité. PhD thesis, Aix-Marseille Université.Google Scholar
Sartor, F., Mettot, C., Bur, R. & Sipp, D. 2015 Unsteadiness in transonic shock-wave/boundary-layer interactions: experimental investigation and global stability analysis. J. Fluid Mech. 781, 550–577.Google Scholar
Schlichting, H. 1979 Boundary-Layer Theory, 6th edn; translation by Kestin J. chaps 14 and 20. AIAA.Google Scholar
Spalart, P. R. & Allmaras, S. R. 1992 A one-equation turbulence model for aerodynamic flows. In 30th Aerospace Sciences Meeting and Exhibit, p. 439. AIAA.Google Scholar
Touber, E. & Sandham, N. D. 2009 Large-eddy simulation of low-frequency unsteadiness in a turbulent shock-induced separation bubble. Theor. Comput. Fluid Dyn. 23 (2), 79–107.Google Scholar
Touber, E. & Sandham, N. D. 2011 Low-order stochastic modelling of low-frequency motions in reflected shock-wave/boundary-layer interactions. J. Fluid Mech. 671, 417–465.Google Scholar
Ünalmis, O. H. & Dolling, D. S. 1994 Decay of wall pressure field and structure of a Mach 5 adiabatic turbulent boundary layer. In AIAA, Fluid Dynamics Conference, 25th, Colorado Springs, CO. AIAA.Google Scholar
Windte, J., Scholz, U. & Radespiel, R. 2006 Validation of the RANS-simulation of laminar separation bubbles on airfoils. Aerosp. Sci. Technol. 10 (6), 484–494.Google Scholar