1 Introduction
A transient resonant structural response due to high-frequency wave-induced loads can be expected to occur for offshore wind turbine columns and support structures. Such turbines are typically located in areas of high winds where they would also be exposed to large waves. The extreme wave loads are found to decompose into a fundamental component at close to the incident wave spectral peak frequency and higher harmonics of this linear component. These higher harmonics occur at frequencies that are close to integer multiples of the fundamental frequency due to nonlinearity in both the incident waves and in the wave–structure interactions. The contributions of second- and third-harmonic wave loads to this resonant excitation, known as ‘springing’ and ‘ringing’, have been discussed by Faltinsen, Newman & Vinje (Reference Faltinsen, Newman and Vinje1995) and Malenica & Molin (Reference Malenica and Molin1995). Gurley & Kareem (Reference Gurley and Kareem1998) associated the cumulative effect of higher water particle velocities in steep waves with ringing of the vertical column. Tromans, Swan & Masterton (Reference Tromans, Swan and Masterton2006) found that there is a close link between high-frequency forces on the vertical cylinder and scattering of high-frequency waves around the cylinder. The high-frequency forces include nonlinear force components up to at least the fifth harmonic of the incoming waves. Grue, Bjørshol & Strand (Reference Grue, Bjørshol and Strand1993), Chaplin, Rainey & Yemm (Reference Chaplin, Rainey and Yemm1997) and Grue & Huseby (Reference Grue and Huseby2002) investigated the ringing response of vertical cylinders in laboratory experiments, and found that a secondary load cycle might have an important effect on the ringing response. A Fourier series expansion in force history suggests that there is a relationship between the occurrence of the secondary load cycle and the appearance of a pronounced higher harmonic force. Numerical investigations were presented by Paulsen et al. (Reference Paulsen, Bredmose, Bingham and Jacobsen2014), and these confirm that the secondary load cycle is associated with the fifth- and sixth-harmonic force components. Thus, accurate extraction of the harmonic structure of the extreme wave loading is important. In addition, other parameters that might affect ringing responses have been identified, such as variable cylinder wetting (Natvig Reference Natvig1994) and the height of the centre of gravity of the structure (Chaplin et al. Reference Chaplin, Rainey and Yemm1997).
The importance of high-order nonlinear wave loading on offshore wind turbine foundations and the effect of seabed slope on the peak wave loading on such structures are studied experimentally in this paper. Unlike most previous experiments, focused wave groups rather than regular or random waves were generated in our model tests for investigating extreme events impacting on an offshore structure. The use of periodic waves with the wave height and period corresponding to some extreme conditions does not consider the random and spectral broadband properties of ocean waves, and might lead to inaccuracy in the estimation in fluid loads for practical applications (Tromans, Anaturak & Hagenmeijer Reference Tromans, Anaturak and Hagenmeijer1991). The realization of prolonged random sea states in the laboratory is very inefficient, although this gives a much better representation of the broadband nature of real ocean waves. Reflection of waves in finite-sized wave tanks is another issue that limits the use of random waves. A focused wave group in which both the amplitude and phase of the Fourier components are carefully controlled is a good alternative, which overcomes some of these shortcomings. It has been widely used in the field of offshore engineering for studying extreme events from a given random sea state of known spectral content. The investigations presented by Jonathan & Taylor (Reference Jonathan and Taylor1997), and Zang et al. (Reference Zang, Gibson, Taylor, Eatock Taylor and Swan2006) indicate that the linear and bound harmonic contributions to large ocean waves and their local interaction with a body can be captured quite accurately by using the focused wave group technique. Bredmose & Jacobsen (Reference Bredmose, Jacobsen, Walsh, Sethi and Kosowatz2011) investigated breaking wave loads on a monopile foundation numerically by application of the focused wave group technique consistent with a Joint North Sea Wave Project (JONSWAP) sea state. The focused wave groups based on an energy density spectrum derived from field data and also a theoretical Gaussian spectrum have been applied to define the inputs to the physical and numerical models by Vyzikas et al. (Reference Vyzikas, Ransley, Hann, Magagna, Greaves, Simmonds, Magar and Conley2013) and Stagonas, Buldakov & Simons (Reference Stagonas, Buldakov, Simons and Lynett2014), respectively.
The use of focused wave groups allows extraction of the higher harmonics in wave–structure interactions by using the ‘phase-inversion’ method described by Baldock, Swan & Taylor (Reference Baldock, Swan and Taylor1996), Hunt et al. (Reference Hunt, Taylor, Borthwick, Stansby and Feng2004), Borthwick et al. (Reference Borthwick, Hunt, Feng, Taylor and Stansby2006) and Zang et al. (Reference Zang, Gibson, Taylor, Eatock Taylor and Swan2006, Reference Zang, Liu, Eatock Taylor and Taylor2009), and more recently generalized by Fitzgerald et al. (Reference Fitzgerald, Taylor, Eatock Taylor, Grice and Zang2014). The ‘phase-inversion’ method assumes that there is a generalized Stokes-like perturbation expansion in focused wave groups and responses. Hence, a decomposition of the total force into odd and even harmonics by making use of the phase difference in incident focused waves is possible. The odd terms contain linear components: third harmonic, fifth harmonic etc. Likewise, the even terms only contain second-harmonic difference, second-harmonic sum, fourth harmonic, and so on. The higher harmonic nonlinear contributions to the wave loads can then be extracted by digital frequency filtering. This technique, utilized by Zang et al. (Reference Zang, Taylor, Morgan, Tello, Grice, Orsaghova, Penchev and Pinto2010) among others, was shown to be appropriate in describing the dynamics of the interaction.
The main purpose of the experiments presented here was to investigate the loading driving a ringing response of a model offshore wind turbine foundation on a flat bed, with emphasis on accurate extraction of the harmonic structure of the extreme wave loads. The cylinder was also located midway up a 1 : 20 plane slope with the same local water depth as the flat bed tests to investigate the effect of the sloping bed on the nature of the incident waves and the loading on the cylinder. It is our aim that the well-documented experimental data should reveal the important physics and also provide a useful dataset for validating existing numerical methods such as computational fluid dynamic codes (CFD) based on the Navier–Stokes equations (Chen et al. Reference Chen, Zang, Hillis, Morgan and Plummer2014), potential-flow solvers both to second order in the frequency domain (Sun et al. Reference Sun, Zang, Chen, Eatock Taylor and Taylor2016) and fully nonlinear in the time domain (Fitzgerald et al. Reference Fitzgerald, Taylor, Eatock Taylor, Grice and Zang2014). This paper is organized as follows. The experimental set-up is described in § 2. In §§ 3 and 4 the underlying assumptions and mathematical principles of the two-phase harmonic separation method are summarized briefly. The application of this separation method to experimental data is presented in § 5 and the effect of bed slope on the measured forces is investigated in § 6. In §§ 7 and 8, the harmonic structure of the hydrodynamic force is investigated using the Huseby and Grue scalings. Finally, § 9 contains the main conclusions.
2 Experiments
2.1 Experimental set-up
A series of model tests on wave–structure interactions was carried out at the Danish Hydraulic Institute (DHI), Denmark. The shallow water basin measuring 35 m by 25 m was used, with a constant water depth of 0.505 m above a flat bed. An array of 36 numerically controlled piston-type wave paddles was used to generate various experimental conditions of interest, including regular waves and unidirectional and bidirectional wave groups with a specified set of frequency components. A single vertical cylinder of diameter 0.25 m (radius
![]() $R=0.125~\text{m}$
) was located 7.8 m from the wave paddles in the centre of the basin. This was supported from above by a stiff triangular frame via four load cells at the top of the column. There was a thin gap of 1 mm between the bottom of the cylinder and the basin floor, permitting measurement of the total horizontal force via the load cells at the top.
$R=0.125~\text{m}$
) was located 7.8 m from the wave paddles in the centre of the basin. This was supported from above by a stiff triangular frame via four load cells at the top of the column. There was a thin gap of 1 mm between the bottom of the cylinder and the basin floor, permitting measurement of the total horizontal force via the load cells at the top.
In addition, a sloping 1-in-20 smooth cement bed was installed. The slope began 6 m upstream of the centre of the cylinder, and terminated before emerging from the water, with the crest of the slope at a depth of 0.2 m before a vertical downward step in the bed. The water depth at the wave paddle was 0.8 m, which reduced to 0.5 m at the centre of the cylinder after 6 m of the slope, allowing comparison of results with the flat bed cases. The schematic overview of the experimental set-up is shown in figure 1.
![]() $R=0.125~\text{m}$
is the radius of the cylinder.
$R=0.125~\text{m}$
is the radius of the cylinder.

Figure 1. The schematic overview of the experimental set-up.
The incident wave field characterized in § 2.2 was based on the records at wave gauge 9 (WG9) for tests without the cylinder in place. The layout of the wave gauges can be seen in figure 2. WG19, which was placed 7.8 m away from the wave paddle and 3 m off the centre line, was almost completely unaffected by scattering of waves from the column. Thus, this gauge was used to check the repeatability of wave runs with and without the cylinder in place. Excellent repeatability was achieved until times after the main group had passed the cylinder and weak scattered components propagated far to the gauge.
Figure 3(a) also shows that the cylinder was surrounded by an array of wave gauges. Also visible in figure 3(a) is the strain gauge array at the top of the cylinder which was used to measure the total horizontal load applied to support the entire dynamic system. A linear force transfer function was derived to extract the hydrodynamic force from the measured total force signal. This is to be discussed in more detail later. Additionally, wave-induced pressures were measured at four vertical locations on the upstream stagnation line on the cylinder, and the wave kinematics adjacent to the column were measured with an acoustic Doppler velocimeter (ADV). This paper is focused on the wave loads on the cylinder.
The consequent violent impact induced by an incident breaking wave is shown in figure 3(b). The wave impact against the cylinder causes a mass of water to be projected vertically upwards as a thin sheet of water which wrapped around the upstream half of the cylinder, seen in figure 3(b). Such sheets have also been reported by Chaplin et al. (Reference Chaplin, Rainey and Yemm1997) and Stansberg et al. (Reference Stansberg, Baarholm, Kristiansen, Hansen and Rortveit2005), among others, in their experiments. A recent study of breaking wave loads on monopiles is reported by Stansby, Devaney & Stallard (Reference Stansby, Devaney and Stallard2013).

Figure 2. The arrangement of wave gauges in the water basin.

Figure 3. The experimental set-up (a) and a violent wave event on the cylinder induced by an incident breaking wave (b). Photos were taken by Henrik Bredmose of DTU.
2.2 Incident wave field
A range of wave conditions with varying wave steepness and spectral peak wave frequencies were tested. The wave steepness was varied from very small, close-to-linear waves up to spilling and plunging breakers. A focused wave group (NewWave) consistent with a JONSWAP spectrum with
![]() $\unicode[STIX]{x1D6FE}=3.3$
was used because it has proved to be a good representation for large waves in severe storms in the North Sea (Taylor & Williams Reference Taylor and Williams2004). The use of focused wave groups provides a model for transient events. It has the advantage that the experimental results are not contaminated by reflected waves over the time of interest, as discussed in Chen et al. (Reference Chen, Zang, Hillis, Morgan and Plummer2014). In this context we take the average shape of a large event in a linear random Gaussian process to be described by the autocorrelation function of that process (Lindgren Reference Lindgren1970; Boccotti Reference Boccotti1983), so the required wave profile in time at the focus point is simply the cosine Fourier transform of the energy spectrum in frequency for the assumed underlying linear process. We also assume that such a wave group can be constructed at the cylinder by using linear paddle generation and the linear dispersion equation. In addition to unidirectional waves, the paddles were set up to generate two identical wave groups crossing with a wave direction of
$\unicode[STIX]{x1D6FE}=3.3$
was used because it has proved to be a good representation for large waves in severe storms in the North Sea (Taylor & Williams Reference Taylor and Williams2004). The use of focused wave groups provides a model for transient events. It has the advantage that the experimental results are not contaminated by reflected waves over the time of interest, as discussed in Chen et al. (Reference Chen, Zang, Hillis, Morgan and Plummer2014). In this context we take the average shape of a large event in a linear random Gaussian process to be described by the autocorrelation function of that process (Lindgren Reference Lindgren1970; Boccotti Reference Boccotti1983), so the required wave profile in time at the focus point is simply the cosine Fourier transform of the energy spectrum in frequency for the assumed underlying linear process. We also assume that such a wave group can be constructed at the cylinder by using linear paddle generation and the linear dispersion equation. In addition to unidirectional waves, the paddles were set up to generate two identical wave groups crossing with a wave direction of
![]() $\unicode[STIX]{x1D6FD}=\pm 20^{\circ }$
so that they impact the cylinder simultaneously, giving a very violent wave–structure interaction.
$\unicode[STIX]{x1D6FD}=\pm 20^{\circ }$
so that they impact the cylinder simultaneously, giving a very violent wave–structure interaction.
In order to apply the separation method presented by Jonathan & Taylor (Reference Jonathan and Taylor1997) to extract the harmonic structure of wave loading on the cylinder, both crest focused waves (C) and trough focused waves (T) were generated in pairs. C and T have the same frequency content but a phase difference of
![]() $180^{\circ }$
(
$180^{\circ }$
(
![]() $\unicode[STIX]{x03C0}$
rads). In these experiments, T can be obtained by multiplying the paddle signal by (
$\unicode[STIX]{x03C0}$
rads). In these experiments, T can be obtained by multiplying the paddle signal by (
![]() $-1$
), assuming linear wave generation in the tank. All wave groups were approximately focused at the front stagnation point of the cylinder, 7.8 m away from the wave paddles. There was some shift in this focusing due to the nonlinear dispersion of the wave groups between the paddle and the cylinder, predominately third-order wave–wave interaction, see Baldock et al. (Reference Baldock, Swan and Taylor1996), so that this did not affect the relative phasing between the C and T groups. As a consequence, some of the recorded wave groups were focused better than others and there was a discrepancy between the target and measured linear crest value of the incident focused wave at the desired focal point.
$-1$
), assuming linear wave generation in the tank. All wave groups were approximately focused at the front stagnation point of the cylinder, 7.8 m away from the wave paddles. There was some shift in this focusing due to the nonlinear dispersion of the wave groups between the paddle and the cylinder, predominately third-order wave–wave interaction, see Baldock et al. (Reference Baldock, Swan and Taylor1996), so that this did not affect the relative phasing between the C and T groups. As a consequence, some of the recorded wave groups were focused better than others and there was a discrepancy between the target and measured linear crest value of the incident focused wave at the desired focal point.
The undisturbed wave field was characterized at the position where the cylinder would be mounted. Based on the time series at WG9, which is the intended focal point in the absence of the cylinder, the actual peak of the linear envelope in time can be obtained using the ‘phase-inversion’ separation method. This is defined as
![]() $A_{f}$
in this paper. Correspondingly, the wavenumber at the focal point based on the frequency of the incident spectral peak energy
$A_{f}$
in this paper. Correspondingly, the wavenumber at the focal point based on the frequency of the incident spectral peak energy
![]() $f_{p}$
is labelled as
$f_{p}$
is labelled as
![]() $k_{f}$
. For each matching crest and trough wave group, the wave slope
$k_{f}$
. For each matching crest and trough wave group, the wave slope
![]() $A_{f}k_{f}$
at the focal point is listed in table 1. It can be seen that the ratio of the actual peak of the linear envelope to the cylinder radius
$A_{f}k_{f}$
at the focal point is listed in table 1. It can be seen that the ratio of the actual peak of the linear envelope to the cylinder radius
![]() $A_{f}/R$
is up to 1, corresponding to the ratio of the maximum wave height (
$A_{f}/R$
is up to 1, corresponding to the ratio of the maximum wave height (
![]() $H$
) of the incoming waves to the cylinder radius
$H$
) of the incoming waves to the cylinder radius
![]() $\max (H)/R\sim 2$
. And the cylinder size
$\max (H)/R\sim 2$
. And the cylinder size
![]() $(k_{f}R)$
ranges from 0.188 to 0.753. This is relevant to the field scale conditions where the dynamic responses are expected to occur, i.e.
$(k_{f}R)$
ranges from 0.188 to 0.753. This is relevant to the field scale conditions where the dynamic responses are expected to occur, i.e.
![]() $kR$
values are typically approximately (0.15–0.3) and the wave height is comparable to the cylinder diameter.
$kR$
values are typically approximately (0.15–0.3) and the wave height is comparable to the cylinder diameter.
Table 1. Incoming wave fields for both the flat and sloping bed cases.

2.3 Hydrodynamic force
Four load cells were used to measure the total horizontal force between the top of the cylinder and the support frame. This force includes both the hydrodynamic force from the incident wave and the effects of the cylinder dynamics. These dynamic effects on the total force must be removed to allow estimation of the pure hydrodynamic load on the cylinder. The structural resonant peak cannot simply be removed from the signal with a low-pass filter because the high-frequency components that excite ‘ringing’ are of considerable interest for the hydrodynamic analysis.
Assuming that the cylinder set-up can be modelled as a simple spring–mass-damper system, a simple linear transfer function
![]() $TF$
can be defined to allow the removal of the additional part of the force reaction into the support frame due to the structural vibration,
$TF$
can be defined to allow the removal of the additional part of the force reaction into the support frame due to the structural vibration,
where
![]() $\unicode[STIX]{x1D714}_{0}$
is the resonant frequency and
$\unicode[STIX]{x1D714}_{0}$
is the resonant frequency and
![]() $\unicode[STIX]{x1D701}$
is the linear structural damping coefficient, which can be estimated by a ‘push’ test. One of the effects of the transfer function (2.1) is to introduce a frequency-dependent phase shift, this is accounted for in the damping term. The inferred damping value includes both structural and fluid damping. In the ‘push’ test, the cylinder was forced to displace by applying a horizontal steady force by hand, and then suddenly removing the force to allow the cylinder to oscillate freely in still water until the motion ceased. The total horizontal force reaction for the cylinder was recorded and used to obtain the resonant frequency and the structural damping by using the fast Fourier transform (FFT) analysis. The values of
$\unicode[STIX]{x1D701}$
is the linear structural damping coefficient, which can be estimated by a ‘push’ test. One of the effects of the transfer function (2.1) is to introduce a frequency-dependent phase shift, this is accounted for in the damping term. The inferred damping value includes both structural and fluid damping. In the ‘push’ test, the cylinder was forced to displace by applying a horizontal steady force by hand, and then suddenly removing the force to allow the cylinder to oscillate freely in still water until the motion ceased. The total horizontal force reaction for the cylinder was recorded and used to obtain the resonant frequency and the structural damping by using the fast Fourier transform (FFT) analysis. The values of
![]() $\unicode[STIX]{x1D714}_{0}$
and
$\unicode[STIX]{x1D714}_{0}$
and
![]() $\unicode[STIX]{x1D701}$
were found to be
$\unicode[STIX]{x1D701}$
were found to be
![]() $23.5~\text{rad}~\text{s}^{-1}$
(3.88 Hz) and 0.009, respectively, valid for the entire decay. The transfer function
$23.5~\text{rad}~\text{s}^{-1}$
(3.88 Hz) and 0.009, respectively, valid for the entire decay. The transfer function
![]() $TF$
is convolved with the total horizontal support force signal. Then a good estimate of the hydrodynamic force time history can be obtained by simply performing an inverse FFT calculation. Spectral components above 6.5 Hz are removed. This is the highest frequency that contains the fifth-harmonic information for the shortest wave case.
$TF$
is convolved with the total horizontal support force signal. Then a good estimate of the hydrodynamic force time history can be obtained by simply performing an inverse FFT calculation. Spectral components above 6.5 Hz are removed. This is the highest frequency that contains the fifth-harmonic information for the shortest wave case.
Figure 4 shows the force spectra and time histories for incident focused wave groups with peak frequency
![]() $f_{p}=0.61~\text{Hz}$
and actual linearized peak amplitude
$f_{p}=0.61~\text{Hz}$
and actual linearized peak amplitude
![]() $A_{f}=0.090~\text{m}$
(
$A_{f}=0.090~\text{m}$
(
![]() $k_{f}A_{f}=0.177$
). The vertical axis is the energy spectral density of force (Force ESD), which is a square of amplitude of each Fourier component. The results for both trough and crest focused wave groups are included. It can be seen that the obvious resonant peak from the measured data at 3.88 Hz has been removed by applying the structural response transfer function. Accordingly, the structural oscillations in the time histories have been removed, leaving a much smoother signal for the hydrodynamic loading. It is striking how much structural dynamics is induced by the crest focused wave impact and how little by the equivalent trough focused case, for this example.
$k_{f}A_{f}=0.177$
). The vertical axis is the energy spectral density of force (Force ESD), which is a square of amplitude of each Fourier component. The results for both trough and crest focused wave groups are included. It can be seen that the obvious resonant peak from the measured data at 3.88 Hz has been removed by applying the structural response transfer function. Accordingly, the structural oscillations in the time histories have been removed, leaving a much smoother signal for the hydrodynamic loading. It is striking how much structural dynamics is induced by the crest focused wave impact and how little by the equivalent trough focused case, for this example.

Figure 4. Force spectra and time histories for both crest and trough focused wave groups, before and after the transfer function is applied to remove the ‘ringing response’. ESD: energy spectral density. The frequency of the incident peak energy
![]() $f_{p}=0.61~\text{Hz}$
and the crest value of the incident focused wave group
$f_{p}=0.61~\text{Hz}$
and the crest value of the incident focused wave group
![]() $A_{f}=0.090~\text{m}$
(
$A_{f}=0.090~\text{m}$
(
![]() $k_{f}A_{f}=0.177$
). Note the vertical flip of the trough focused force signal.
$k_{f}A_{f}=0.177$
). Note the vertical flip of the trough focused force signal.
2.4 Strong nonlinearity
Both unidirectional groups and a bidirectional pair of unidirectional groups with directions at
![]() $\unicode[STIX]{x1D6FD}=\pm 20^{\circ }$
to the tank central line are studied. Figure 5 shows force time histories for wave groups hitting the cylinder on the flat bed, and the corresponding force and elevation spectra. The frequency of the peak spectral energy is 0.49 Hz and the peak of the linear wave envelope is 0.101 m (
$\unicode[STIX]{x1D6FD}=\pm 20^{\circ }$
to the tank central line are studied. Figure 5 shows force time histories for wave groups hitting the cylinder on the flat bed, and the corresponding force and elevation spectra. The frequency of the peak spectral energy is 0.49 Hz and the peak of the linear wave envelope is 0.101 m (
![]() $k_{f}A_{f}=0.152$
). The time histories of the free-surface elevation at the focal point in the absence of the cylinder are shown in figure 5(a,c) and the horizontal forces on the cylinder are shown in figure 5(b,d). Figure 5(a,b) shows the results for the unidirectional case and figure 5(c,d) shows the results for the bidirectional case. Each of the two component wave groups used to produce the bidirectional wave in figure 5(c,d) is the same as that shown figure 5(a,b). Spectra for the incident wave surface elevation and the resulting force for the bidirectional case are shown in figure 5(e,f). For the bidirectional groups, the time series and the corresponding spectra after the transfer function is applied are also shown in the plots. It can be seen from the free-surface motions that the two identical wave groups combined to hit the cylinder simultaneously, giving a combined breaking wave of approximately twice the height of the individual groups. The shape of the force time signal for the bidirectional input waves is very different from that for the unidirectional wave. The associated force spectrum is much flatter with increasing frequency than the surface elevation spectrum, showing that the harmonics are much more important. The strong local oscillations in the force time histories for the bidirectional case suggest there exist large higher frequency force components which trigger a vigorous ringing response of the structure.
$k_{f}A_{f}=0.152$
). The time histories of the free-surface elevation at the focal point in the absence of the cylinder are shown in figure 5(a,c) and the horizontal forces on the cylinder are shown in figure 5(b,d). Figure 5(a,b) shows the results for the unidirectional case and figure 5(c,d) shows the results for the bidirectional case. Each of the two component wave groups used to produce the bidirectional wave in figure 5(c,d) is the same as that shown figure 5(a,b). Spectra for the incident wave surface elevation and the resulting force for the bidirectional case are shown in figure 5(e,f). For the bidirectional groups, the time series and the corresponding spectra after the transfer function is applied are also shown in the plots. It can be seen from the free-surface motions that the two identical wave groups combined to hit the cylinder simultaneously, giving a combined breaking wave of approximately twice the height of the individual groups. The shape of the force time signal for the bidirectional input waves is very different from that for the unidirectional wave. The associated force spectrum is much flatter with increasing frequency than the surface elevation spectrum, showing that the harmonics are much more important. The strong local oscillations in the force time histories for the bidirectional case suggest there exist large higher frequency force components which trigger a vigorous ringing response of the structure.
The possibility of the excitation of the ‘ringing’ response of the cylinder due to the higher-order forces beyond the second harmonic of the incident waves is clear. These effects have been investigated previously by many authors, including Faltinsen et al. (Reference Faltinsen, Newman and Vinje1995), Newman (Reference Newman, Grue, Gjevik and Weber1996) and Chaplin et al. (Reference Chaplin, Rainey and Yemm1997). It is worth noting that not only the large third-order component as described in the Faltinsen–Newman–Vinje potential-flow model (FNV model) (Faltinsen et al. Reference Faltinsen, Newman and Vinje1995) but also fourth- and fifth-harmonic excitation were observed in our model tests and by many others. The FNV model only predicts hydrodynamic loads up to third order from weakly nonlinear wave kinematics.

Figure 5. Wave forces on the cylinder: incident wave time histories (a,c) and horizontal forces on the cylinder (b,d), for a unidirectional group (a,b) and a bidirectional pair
![]() $\pm 20^{\circ }$
(c,d). (e,f) Incident wave surface elevation energy spectrum (e), force energy spectrum (f), both for a bidirectional incident wave pair only. The frequency of the incident peak energy
$\pm 20^{\circ }$
(c,d). (e,f) Incident wave surface elevation energy spectrum (e), force energy spectrum (f), both for a bidirectional incident wave pair only. The frequency of the incident peak energy
![]() $f_{p}=0.49~\text{Hz}$
and the crest value of the incident focused wave group
$f_{p}=0.49~\text{Hz}$
and the crest value of the incident focused wave group
![]() $A_{f}=0.101~\text{m}$
(
$A_{f}=0.101~\text{m}$
(
![]() $k_{f}A_{f}=0.152$
).
$k_{f}A_{f}=0.152$
).
3 The harmonic structure of the hydrodynamic force
For a regular wave the surface elevation can be written in non-dimensional form as
where the linear phase function is
![]() $\cos \unicode[STIX]{x1D703}$
and the wave amplitude is
$\cos \unicode[STIX]{x1D703}$
and the wave amplitude is
![]() $A$
. The radius of the cylinder is
$A$
. The radius of the cylinder is
![]() $R$
. The second-order coefficient of this Stokes series is
$R$
. The second-order coefficient of this Stokes series is
![]() $S_{EE2}$
, the number in the subscript denoting that this is a second-order term, and the subscripts
$S_{EE2}$
, the number in the subscript denoting that this is a second-order term, and the subscripts
![]() $EE$
denoting the second-order free-surface elevation written in terms of the linear elevation.
$EE$
denoting the second-order free-surface elevation written in terms of the linear elevation.
For regular waves on deep water we have
![]() $S_{EE2}=(1/2)kR$
and
$S_{EE2}=(1/2)kR$
and
![]() $S_{EE3}=(3/8)(kR)^{2}$
. Of course introducing the cylinder radius
$S_{EE3}=(3/8)(kR)^{2}$
. Of course introducing the cylinder radius
![]() $R$
is not necessary for the free-surface elevation.
$R$
is not necessary for the free-surface elevation.
We generalize (3.1) to a slowly varying wave group, i.e.
![]() $\cos \unicode[STIX]{x1D703}$
is equivalent to
$\cos \unicode[STIX]{x1D703}$
is equivalent to
![]() $\unicode[STIX]{x1D702}_{1}$
, the double-frequency term
$\unicode[STIX]{x1D702}_{1}$
, the double-frequency term
![]() $\cos (2\unicode[STIX]{x1D703})$
is equivalent to
$\cos (2\unicode[STIX]{x1D703})$
is equivalent to
![]() $(\unicode[STIX]{x1D702}_{1}^{2}-\unicode[STIX]{x1D702}_{1H}^{2})$
etc., where
$(\unicode[STIX]{x1D702}_{1}^{2}-\unicode[STIX]{x1D702}_{1H}^{2})$
etc., where
![]() $\unicode[STIX]{x1D702}_{1}$
is the linear time history of the free-surface elevation and
$\unicode[STIX]{x1D702}_{1}$
is the linear time history of the free-surface elevation and
![]() $\unicode[STIX]{x1D702}_{1H}$
its Hilbert (
$\unicode[STIX]{x1D702}_{1H}$
its Hilbert (
![]() $90^{\circ }$
shifted) transform. The Hilbert transform is used to shift by
$90^{\circ }$
shifted) transform. The Hilbert transform is used to shift by
![]() $90^{\circ }$
every Fourier component within a signal. This is a generalization of
$90^{\circ }$
every Fourier component within a signal. This is a generalization of
![]() $\cos (\unicode[STIX]{x1D703})\rightarrow \sin (\unicode[STIX]{x1D703})$
for a single component. The linear term
$\cos (\unicode[STIX]{x1D703})\rightarrow \sin (\unicode[STIX]{x1D703})$
for a single component. The linear term
![]() $\unicode[STIX]{x1D702}_{1}$
is non-dimensional. The peak value of the envelope in time is unity. The variation of
$\unicode[STIX]{x1D702}_{1}$
is non-dimensional. The peak value of the envelope in time is unity. The variation of
![]() $\unicode[STIX]{x1D702}_{1}$
in time captures both the phase and group effects. Thus the free-surface elevation is approximated as
$\unicode[STIX]{x1D702}_{1}$
in time captures both the phase and group effects. Thus the free-surface elevation is approximated as
The terms in square brackets are double- and triple-frequency terms with
![]() $\unicode[STIX]{x1D703}=0$
crests in phase with those of the linear component
$\unicode[STIX]{x1D703}=0$
crests in phase with those of the linear component
![]() $\unicode[STIX]{x1D702}_{1}$
.
$\unicode[STIX]{x1D702}_{1}$
.
In experiments, we can run a pair of wave cases, a crest focused wave group and an inverted trough focused group, by multiplying the linear paddle signal by (
![]() $-1$
). This can be viewed as
$-1$
). This can be viewed as
![]() $A\rightarrow (-A)$
, or equivalently the phase
$A\rightarrow (-A)$
, or equivalently the phase
![]() $\unicode[STIX]{x1D703}\rightarrow (\unicode[STIX]{x1D703}+\unicode[STIX]{x03C0})$
. Then
$\unicode[STIX]{x1D703}\rightarrow (\unicode[STIX]{x1D703}+\unicode[STIX]{x03C0})$
. Then
Equations (3.3) and (3.4) have only odd and even harmonics, respectively. For irregular waves, this combination is helpful for identifying the individual harmonics.
For the force exerted on a vertical surface-piercing cylinder, we use the Huseby and Grue scaling
![]() $\unicode[STIX]{x1D70C}gR^{3}(A/R)^{n}$
for the
$\unicode[STIX]{x1D70C}gR^{3}(A/R)^{n}$
for the
![]() $n$
th-order harmonic force.
$n$
th-order harmonic force.
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $g$
are the water density and the acceleration due to gravity, respectively. We write a Stokes-like approximation for the total in-line hydrodynamic force as
$g$
are the water density and the acceleration due to gravity, respectively. We write a Stokes-like approximation for the total in-line hydrodynamic force as
with
![]() $(\unicode[STIX]{x1D6FC}_{FEn}^{2}+\unicode[STIX]{x1D6FD}_{FEn}^{2})=1$
.
$(\unicode[STIX]{x1D6FC}_{FEn}^{2}+\unicode[STIX]{x1D6FD}_{FEn}^{2})=1$
.
These
![]() $(\unicode[STIX]{x1D6FC}_{FEn},\unicode[STIX]{x1D6FD}_{FEn})$
terms represent phase shifts between the nonlinear harmonics of force and elevation. The subscripts of the Stokes-like coefficients
$(\unicode[STIX]{x1D6FC}_{FEn},\unicode[STIX]{x1D6FD}_{FEn})$
terms represent phase shifts between the nonlinear harmonics of force and elevation. The subscripts of the Stokes-like coefficients
![]() $S_{FEn}$
show that these relate the force in terms of the surface elevation for the
$S_{FEn}$
show that these relate the force in terms of the surface elevation for the
![]() $n$
th harmonic. Of course for a sufficiently slender cylinder,
$n$
th harmonic. Of course for a sufficiently slender cylinder,
![]() $S_{FE1}$
becomes the linear inertia coefficient from the Morison equation. This form is equivalent to that used by Newman (Reference Newman, Grue, Gjevik and Weber1996) for the generalization of the FNV model for irregular waves, except that we neglect the nonlinear subharmonic components such as the second-order frequency difference term.
$S_{FE1}$
becomes the linear inertia coefficient from the Morison equation. This form is equivalent to that used by Newman (Reference Newman, Grue, Gjevik and Weber1996) for the generalization of the FNV model for irregular waves, except that we neglect the nonlinear subharmonic components such as the second-order frequency difference term.
For the detailed comparisons of the structure of the force harmonics, we use an alternative version of (3.5) where the phase functions are based on the linear force component,
Since phase is now defined relative to that of the linear force, the first term reduces to
![]() $[f_{1}]$
and the linear force can be written as
$[f_{1}]$
and the linear force can be written as
![]() $F_{1}=S_{FE1}\unicode[STIX]{x1D70C}gR^{2}A[f_{1}]$
. We test the structure of this form (3.6) against experimental measurements by:
$F_{1}=S_{FE1}\unicode[STIX]{x1D70C}gR^{2}A[f_{1}]$
. We test the structure of this form (3.6) against experimental measurements by:
(1) the term by term scalings in wave amplitude
 $(A/R)^{n}$
;
$(A/R)^{n}$
;(2) the location and shape in time of the envelope of the
 $n$
th-harmonic force against the envelope of the linear force component to the
$n$
th-harmonic force against the envelope of the linear force component to the
 $n$
th power
$n$
th power
 $(f_{1}^{2}+f_{1H}^{2})^{(n/2)}$
;
$(f_{1}^{2}+f_{1H}^{2})^{(n/2)}$
;(3) and the phasing of the
 $n$
th harmonic of force to a least-squares-fitted approximation for the
$n$
th harmonic of force to a least-squares-fitted approximation for the
 $n$
th-harmonic phase function using
$n$
th-harmonic phase function using
 $\unicode[STIX]{x1D6FC}_{FFn}$
and
$\unicode[STIX]{x1D6FC}_{FFn}$
and
 $\unicode[STIX]{x1D6FD}_{FFn}$
.
$\unicode[STIX]{x1D6FD}_{FFn}$
.
Finally in § 8 we show that our hypothetical form for the entire harmonic structure can be written in terms of the linear component of force alone, with no reference to the associated undisturbed free-surface elevation at the position of the loaded cylinder. This form is as follows. We write the linear component as
where
![]() ${\mathcal{F}}_{1}$
is the peak value of the envelope of
${\mathcal{F}}_{1}$
is the peak value of the envelope of
![]() $F_{1}$
in time and
$F_{1}$
in time and
![]() $f_{1}$
carries all the phase information and group structure as previously. Then the assumed form for the total force in time becomes
$f_{1}$
carries all the phase information and group structure as previously. Then the assumed form for the total force in time becomes
 $$\begin{eqnarray}\displaystyle \frac{F}{\unicode[STIX]{x1D70C}gR^{3}} & = & \displaystyle \frac{{\mathcal{F}}_{1}}{\unicode[STIX]{x1D70C}gR^{3}}[f_{1}]+S_{FF2}\left(\frac{{\mathcal{F}}_{1}}{\unicode[STIX]{x1D70C}gR^{3}}\right)^{2}[\unicode[STIX]{x1D6FC}_{FF2}(f_{1}^{2}-f_{1H}^{2})+\unicode[STIX]{x1D6FD}_{FF2}(2f_{1}\,f_{1H})]\nonumber\\ \displaystyle & & \displaystyle +\,S_{FF3}\left(\frac{{\mathcal{F}}_{1}}{\unicode[STIX]{x1D70C}gR^{3}}\right)^{3}[\unicode[STIX]{x1D6FC}_{FF3}f_{1}(f_{1}^{2}-2f_{1H}^{2})+\unicode[STIX]{x1D6FD}_{FF3}(f_{1H}(3f_{1}^{2}-f_{1H}^{2}))]+\cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{F}{\unicode[STIX]{x1D70C}gR^{3}} & = & \displaystyle \frac{{\mathcal{F}}_{1}}{\unicode[STIX]{x1D70C}gR^{3}}[f_{1}]+S_{FF2}\left(\frac{{\mathcal{F}}_{1}}{\unicode[STIX]{x1D70C}gR^{3}}\right)^{2}[\unicode[STIX]{x1D6FC}_{FF2}(f_{1}^{2}-f_{1H}^{2})+\unicode[STIX]{x1D6FD}_{FF2}(2f_{1}\,f_{1H})]\nonumber\\ \displaystyle & & \displaystyle +\,S_{FF3}\left(\frac{{\mathcal{F}}_{1}}{\unicode[STIX]{x1D70C}gR^{3}}\right)^{3}[\unicode[STIX]{x1D6FC}_{FF3}f_{1}(f_{1}^{2}-2f_{1H}^{2})+\unicode[STIX]{x1D6FD}_{FF3}(f_{1H}(3f_{1}^{2}-f_{1H}^{2}))]+\cdots \,.\end{eqnarray}$$
Now the force approximation contains Stokes-like amplitude terms
![]() ${\mathcal{F}}_{1}/(\unicode[STIX]{x1D70C}gR^{3})$
based on the peak amplitude of the linear force component, non-dimensional force coefficients at each order
${\mathcal{F}}_{1}/(\unicode[STIX]{x1D70C}gR^{3})$
based on the peak amplitude of the linear force component, non-dimensional force coefficients at each order
![]() $S_{FFn}$
, and phase coefficients
$S_{FFn}$
, and phase coefficients
![]() $(\unicode[STIX]{x1D6FC}_{FFn},\unicode[STIX]{x1D6FD}_{FFn})$
, with
$(\unicode[STIX]{x1D6FC}_{FFn},\unicode[STIX]{x1D6FD}_{FFn})$
, with
![]() $(\unicode[STIX]{x1D6FC}_{FFn}^{2}+\unicode[STIX]{x1D6FD}_{FFn}^{2})=1$
, as previously.
$(\unicode[STIX]{x1D6FC}_{FFn}^{2}+\unicode[STIX]{x1D6FD}_{FFn}^{2})=1$
, as previously.
4 Data processing
In order to fit the coefficients of the perturbation series (3.6), we need both the undisturbed incident wave field
![]() $\unicode[STIX]{x1D702}$
and the total hydrodynamic load
$\unicode[STIX]{x1D702}$
and the total hydrodynamic load
![]() $F$
. Given that each harmonic for a wave group is spread over a range of frequencies, we make use of the ‘phase-inversion’ method of Baldock et al. (Reference Baldock, Swan and Taylor1996), Hunt et al. (Reference Hunt, Taylor, Borthwick, Stansby and Feng2004), Borthwick et al. (Reference Borthwick, Hunt, Feng, Taylor and Stansby2006) and Zang et al. (Reference Zang, Gibson, Taylor, Eatock Taylor and Swan2006). The crest and trough focused combinations
$F$
. Given that each harmonic for a wave group is spread over a range of frequencies, we make use of the ‘phase-inversion’ method of Baldock et al. (Reference Baldock, Swan and Taylor1996), Hunt et al. (Reference Hunt, Taylor, Borthwick, Stansby and Feng2004), Borthwick et al. (Reference Borthwick, Hunt, Feng, Taylor and Stansby2006) and Zang et al. (Reference Zang, Gibson, Taylor, Eatock Taylor and Swan2006). The crest and trough focused combinations
![]() $(C-T)/2$
for the odd harmonics and
$(C-T)/2$
for the odd harmonics and
![]() $(C+T)/2$
for the even harmonics now have the nonlinear harmonics better separated in frequency. This is shown in (3.3)–(3.4).
$(C+T)/2$
for the even harmonics now have the nonlinear harmonics better separated in frequency. This is shown in (3.3)–(3.4).
Each
![]() $n$
th harmonic is separated out in frequency over a range of
$n$
th harmonic is separated out in frequency over a range of
![]() $f_{p}$
, centred about
$f_{p}$
, centred about
![]() $nf_{p}$
, where
$nf_{p}$
, where
![]() $f_{p}$
is the peak frequency of the fundamental harmonic. There is a ramp down and ramp up at the ends of the filter passband.
$f_{p}$
is the peak frequency of the fundamental harmonic. There is a ramp down and ramp up at the ends of the filter passband.
The ‘phase-inversion’ method described above achieves clean separation only when the crest and trough signals are aligned, occurring at identical times. If the time alignment is not perfect, so the phase difference between these two signals is not
![]() $180^{\circ }$
, the odd and even harmonics cannot be completely separated. Some leakage will then occur from the odd/even harmonics into the assumed even/odd spectra components. In order to minimize the ‘leakage’ resulting from timing misalignment, the minimum of the cross-correlation between crest and trough signals is calculated and the relative time shift to bring them into alignment can be found accordingly. This lack of automatic alignment arose because the wave generation software available at DHI could not be synchronized with the data acquisition system used for the wave gauges and force transducers.
$180^{\circ }$
, the odd and even harmonics cannot be completely separated. Some leakage will then occur from the odd/even harmonics into the assumed even/odd spectra components. In order to minimize the ‘leakage’ resulting from timing misalignment, the minimum of the cross-correlation between crest and trough signals is calculated and the relative time shift to bring them into alignment can be found accordingly. This lack of automatic alignment arose because the wave generation software available at DHI could not be synchronized with the data acquisition system used for the wave gauges and force transducers.
The standard definition of the cross-correlation is used,
where
![]() $F_{xC}$
and
$F_{xC}$
and
![]() $F_{xT}$
are the time series of the horizontal force for crest focused wave groups and trough focused wave groups, respectively.
$F_{xT}$
are the time series of the horizontal force for crest focused wave groups and trough focused wave groups, respectively.
![]() $\unicode[STIX]{x1D70F}$
is the shift in time, and
$\unicode[STIX]{x1D70F}$
is the shift in time, and
![]() $\unicode[STIX]{x1D70F}_{0}$
at which the value of
$\unicode[STIX]{x1D70F}_{0}$
at which the value of
![]() $R_{CT}$
is minimum is the time shift needed to minimize the leakage. The crest and trough signals are band-pass filtered over the range (
$R_{CT}$
is minimum is the time shift needed to minimize the leakage. The crest and trough signals are band-pass filtered over the range (
![]() $0.8f_{p}{-}1.5f_{p}$
) before the correlation function is calculated. This removes almost all of the bound harmonics from the signals.
$0.8f_{p}{-}1.5f_{p}$
) before the correlation function is calculated. This removes almost all of the bound harmonics from the signals.
As an example, the cross-correlation
![]() $R_{CT}(\unicode[STIX]{x1D70F})$
for the focused wave group with peak frequency of 0.49 Hz and actual linearized peak amplitude of 0.101 m (
$R_{CT}(\unicode[STIX]{x1D70F})$
for the focused wave group with peak frequency of 0.49 Hz and actual linearized peak amplitude of 0.101 m (
![]() $k_{f}A_{f}=0.152$
) is shown in figure 6. It can be seen that
$k_{f}A_{f}=0.152$
) is shown in figure 6. It can be seen that
![]() $\unicode[STIX]{x1D70F}_{0}=0.64~\text{s}$
at which
$\unicode[STIX]{x1D70F}_{0}=0.64~\text{s}$
at which
![]() $R_{CT}(\unicode[STIX]{x1D70F})$
is a minimum is the shift required to align the signals. Thus, the crest signal is shifted 0.64 s forwards relative to the trough signal, and the aligned crest and trough signals are shown in figure 7(a). The quality of the alignment can be assessed by examining the spectra of the now separated odd and even harmonics, as shown in figure 7(b). A log-scale is used on the vertical axis to show the low level of the
$R_{CT}(\unicode[STIX]{x1D70F})$
is a minimum is the shift required to align the signals. Thus, the crest signal is shifted 0.64 s forwards relative to the trough signal, and the aligned crest and trough signals are shown in figure 7(a). The quality of the alignment can be assessed by examining the spectra of the now separated odd and even harmonics, as shown in figure 7(b). A log-scale is used on the vertical axis to show the low level of the
![]() $f_{p}$
component in the even harmonics, and the clear separation of the even harmonic peaks in one plot and the odd harmonics in the other. The odd harmonics have obvious peaks in the spectrum at
$f_{p}$
component in the even harmonics, and the clear separation of the even harmonic peaks in one plot and the odd harmonics in the other. The odd harmonics have obvious peaks in the spectrum at
![]() ${\sim}f_{p}$
,
${\sim}f_{p}$
,
![]() $3f_{p}$
,
$3f_{p}$
,
![]() $5f_{p}$
and the even harmonics at
$5f_{p}$
and the even harmonics at
![]() ${\sim}2f_{p}$
,
${\sim}2f_{p}$
,
![]() $4f_{p}$
,
$4f_{p}$
,
![]() $6f_{p}$
, as expected. The filtered spectra for force harmonics up to fifth with the filter windows are shown in figure 8.
$6f_{p}$
, as expected. The filtered spectra for force harmonics up to fifth with the filter windows are shown in figure 8.

Figure 6. The cross-correlation
![]() $R_{CT}(\unicode[STIX]{x1D70F})$
for the focused wave group with a peak frequency of 0.49 Hz and an actual linearized peak amplitude of 0.101 m, with
$R_{CT}(\unicode[STIX]{x1D70F})$
for the focused wave group with a peak frequency of 0.49 Hz and an actual linearized peak amplitude of 0.101 m, with
![]() $k_{f}A_{f}=0.152$
.
$k_{f}A_{f}=0.152$
.

Figure 7. The cross-correlation alignment for the focused wave group with a peak frequency of 0.49 Hz and an actual linearized peak amplitude of 0.101 m, with
![]() $A_{f}k_{f}=0.152$
. (a) Signals aligned, leakage minimized. (b) The separated odd and even harmonic spectra.
$A_{f}k_{f}=0.152$
. (a) Signals aligned, leakage minimized. (b) The separated odd and even harmonic spectra.

Figure 8. The filtered spectra for the focused wave group with a peak frequency of 0.49 Hz and an actual linearized peak amplitude of 0.101 m, with
![]() $A_{f}k_{f}=0.152$
. (a) The separated odd harmonic spectra. (b) The separated even harmonic spectra.
$A_{f}k_{f}=0.152$
. (a) The separated odd harmonic spectra. (b) The separated even harmonic spectra.
The envelopes of the harmonics in time of the wave loading are calculated to display the structure of the force signal in time, and an envelope of a poorly focused wave group is also useful to indicate the time at which the peak of the wave group occurs.
Given the assumption that there is a generalized Stokes-type perturbation expansion for a wave group for both elevation and force, we propose that the envelope of each harmonic starting at second order might be approximated from the envelope of the linear component. The approximated envelopes of
![]() $n$
th harmonics are obtained by raising the fundamental envelope to the power
$n$
th harmonics are obtained by raising the fundamental envelope to the power
![]() $n$
, and are then scaled to fit the measured envelopes of the
$n$
, and are then scaled to fit the measured envelopes of the
![]() $n$
th-harmonic component by a least-squares method. In addition to the envelopes, the actual time history at a higher harmonic can also be approximated by the linear component time history.
$n$
th-harmonic component by a least-squares method. In addition to the envelopes, the actual time history at a higher harmonic can also be approximated by the linear component time history.
As an example of phase identification, we write the measured second-order sum harmonic of force as
where
![]() $f_{2}$
contains the phase and group structure of the measured component
$f_{2}$
contains the phase and group structure of the measured component
![]() $F_{2}$
. This has unit peak amplitude,
$F_{2}$
. This has unit peak amplitude,
![]() ${\mathcal{F}}_{2}$
is the peak value of the envelope of the measured force component
${\mathcal{F}}_{2}$
is the peak value of the envelope of the measured force component
![]() $F_{2}$
. Then using (3.8)
$F_{2}$
. Then using (3.8)
![]() $f_{2}$
is modelled as
$f_{2}$
is modelled as
The phase functions
![]() $(\unicode[STIX]{x1D6FC}_{FF2},\unicode[STIX]{x1D6FD}_{FF2})$
are estimated by
$(\unicode[STIX]{x1D6FC}_{FF2},\unicode[STIX]{x1D6FD}_{FF2})$
are estimated by
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{FF2}=\frac{\displaystyle \int _{t_{1}}^{t_{2}}f_{2}(f_{1}^{2}-f_{1H}^{2})\,\text{d}t}{\displaystyle \int _{t_{1}}^{t_{2}}(f_{1}^{2}-f_{1H}^{2})^{2}\,\text{d}t},\quad \unicode[STIX]{x1D6FD}_{FF2}=\frac{\displaystyle \int _{t_{1}}^{t_{2}}f_{2}(2f_{1}\,f_{1H})\,\text{d}t}{\displaystyle \int _{t_{1}}^{t_{2}}(2f_{1}\,f_{1H})^{2}\,\text{d}t}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{FF2}=\frac{\displaystyle \int _{t_{1}}^{t_{2}}f_{2}(f_{1}^{2}-f_{1H}^{2})\,\text{d}t}{\displaystyle \int _{t_{1}}^{t_{2}}(f_{1}^{2}-f_{1H}^{2})^{2}\,\text{d}t},\quad \unicode[STIX]{x1D6FD}_{FF2}=\frac{\displaystyle \int _{t_{1}}^{t_{2}}f_{2}(2f_{1}\,f_{1H})\,\text{d}t}{\displaystyle \int _{t_{1}}^{t_{2}}(2f_{1}\,f_{1H})^{2}\,\text{d}t}.\end{eqnarray}$$
The limits of the integrals are set by the duration of harmonics. The phase of the harmonic force component relative to the linear force component is then defined as
![]() $\unicode[STIX]{x1D719}_{n}=\arctan (\unicode[STIX]{x1D6FD}_{FF2}/\unicode[STIX]{x1D6FC}_{FF2})$
. Similar expressions for the surface elevation were derived for harmonics of the free-surface elevation by Walker, Taylor & Eatock Taylor (Reference Walker, Taylor and Eatock Taylor2004).
$\unicode[STIX]{x1D719}_{n}=\arctan (\unicode[STIX]{x1D6FD}_{FF2}/\unicode[STIX]{x1D6FC}_{FF2})$
. Similar expressions for the surface elevation were derived for harmonics of the free-surface elevation by Walker, Taylor & Eatock Taylor (Reference Walker, Taylor and Eatock Taylor2004).
5 Spectral decomposition
Figure 9 shows the extracted harmonic structure for two different wave groups using the method described above. These wave groups are based on JONSWAP sea states with
![]() $\unicode[STIX]{x1D6FE}=3.3$
and a peak frequency
$\unicode[STIX]{x1D6FE}=3.3$
and a peak frequency
![]() $f_{p}=0.61~\text{Hz}$
. Figure 9(a) is a unidirectional wave group with actual linearized peak amplitude
$f_{p}=0.61~\text{Hz}$
. Figure 9(a) is a unidirectional wave group with actual linearized peak amplitude
![]() $A_{f}=0.052~\text{m}$
(
$A_{f}=0.052~\text{m}$
(
![]() $k_{f}A_{f}=0.103$
) and figure 9(b) is a unidirectional wave group with actual linearized peak amplitude
$k_{f}A_{f}=0.103$
) and figure 9(b) is a unidirectional wave group with actual linearized peak amplitude
![]() $A_{f}=0.090~\text{m}$
(
$A_{f}=0.090~\text{m}$
(
![]() $k_{f}A_{f}=0.177$
), both on the flat bed.
$k_{f}A_{f}=0.177$
), both on the flat bed.

Figure 9. The harmonic structures of horizontal wave loading on the cylinder and the envelopes for both focused wave groups with
![]() $A_{f}=0.052~\text{m}$
and 0.090 m propagating in a flat bed. The peak frequency
$A_{f}=0.052~\text{m}$
and 0.090 m propagating in a flat bed. The peak frequency
![]() $f_{p}=0.61~\text{Hz}$
. (a) Unidirectional:
$f_{p}=0.61~\text{Hz}$
. (a) Unidirectional:
![]() $A_{f}=0.052~\text{m}$
(
$A_{f}=0.052~\text{m}$
(
![]() $k_{f}A_{f}=0.103$
), (b) unidirectional:
$k_{f}A_{f}=0.103$
), (b) unidirectional:
![]() $A_{f}=0.090~\text{m}$
(
$A_{f}=0.090~\text{m}$
(
![]() $k_{f}A_{f}=0.177$
).
$k_{f}A_{f}=0.177$
).
The top plot in each of the figures is the total horizontal wave loading on the cylinder for both crest and trough focused waves. The crest and trough signals shown here have the best possible alignment to minimize the energy leakage between adjacent force harmonics. The succeeding plots below show the long-wave difference component, linear, second, third, fourth and fifth sum harmonics, respectively. The envelopes of the linear components are obtained based on the envelope of the linear undisturbed free-surface elevation discussed previously. The envelopes of
![]() $n$
th harmonics above second order are obtained by raising the fundamental envelope to the power
$n$
th harmonics above second order are obtained by raising the fundamental envelope to the power
![]() $n$
and are plotted on the top of the corresponding harmonic components in figure 9, after being scaled by a least-squares method to match the size of the maximum of the measured
$n$
and are plotted on the top of the corresponding harmonic components in figure 9, after being scaled by a least-squares method to match the size of the maximum of the measured
![]() $n$
th-order harmonics.
$n$
th-order harmonics.
It can be seen that the applied two-phase separation technique works well for these two cases. The extracted harmonics fit the estimated envelopes fairly well although some discrepancies are found. The slightly mismatch for the linear component in figure 9(a) corresponds to a difference between the envelope of the undisturbed free-surface elevation and the force signal. In particular, the peak in the envelope of the force is slightly delayed by 0.5 s, and these errors for the reconstructed harmonics building up and are, thus, larger for higher harmonics. The error waves from the paddle result in a small secondary pulse observed in the second-order harmonic at approximately
![]() $t=(14{-}19)~\text{s}$
in figure 9. The control signal sent to the paddle was linear while the waves generated were inherently nonlinear. The wiggles of the third-order harmonic are too broad for its approximated envelope, and the peak force does not align well with the peak of the estimated envelope obtained by raising the linear envelope to the third power. Additionally, some later waves in addition to the main packet are observed in the third-order force (more obvious in figure 9
a). This slight mismatch could be due to several factors, such as the third-harmonic term that arises from the
$t=(14{-}19)~\text{s}$
in figure 9. The control signal sent to the paddle was linear while the waves generated were inherently nonlinear. The wiggles of the third-order harmonic are too broad for its approximated envelope, and the peak force does not align well with the peak of the estimated envelope obtained by raising the linear envelope to the third power. Additionally, some later waves in addition to the main packet are observed in the third-order force (more obvious in figure 9
a). This slight mismatch could be due to several factors, such as the third-harmonic term that arises from the
![]() $u|u|$
term in Morison drag, a contribution from nonlinear free-surface ringing forces in potential flow (Faltinsen, Newman & Vinje Reference Faltinsen, Newman, Vinje, Chakrabarti, Pontes, Hisaaki, Falzarano, Schofield and Morrison1996; Chaplin et al.
Reference Chaplin, Rainey and Yemm1997), and the secondary load cycle due to short and steep waves around the surface of the cylinder (Grue & Huseby Reference Grue and Huseby2002). The analysis of (Fitzgerald et al.
Reference Fitzgerald, Taylor, Eatock Taylor, Grice and Zang2014) suggests that even for fully nonlinear potential flow the third harmonic is in a real sense ‘different’ from the others, with extra nonlinear dynamics occurring, supportive of the FNV analysis of (Faltinsen et al.
Reference Faltinsen, Newman, Vinje, Chakrabarti, Pontes, Hisaaki, Falzarano, Schofield and Morrison1996).
$u|u|$
term in Morison drag, a contribution from nonlinear free-surface ringing forces in potential flow (Faltinsen, Newman & Vinje Reference Faltinsen, Newman, Vinje, Chakrabarti, Pontes, Hisaaki, Falzarano, Schofield and Morrison1996; Chaplin et al.
Reference Chaplin, Rainey and Yemm1997), and the secondary load cycle due to short and steep waves around the surface of the cylinder (Grue & Huseby Reference Grue and Huseby2002). The analysis of (Fitzgerald et al.
Reference Fitzgerald, Taylor, Eatock Taylor, Grice and Zang2014) suggests that even for fully nonlinear potential flow the third harmonic is in a real sense ‘different’ from the others, with extra nonlinear dynamics occurring, supportive of the FNV analysis of (Faltinsen et al.
Reference Faltinsen, Newman, Vinje, Chakrabarti, Pontes, Hisaaki, Falzarano, Schofield and Morrison1996).
From figure 9, we see that the shape of higher harmonic loads in time can be matched quite well to the envelope of the linear component raised to the appropriate power. These approximate envelopes for each harmonic can be used to predict the corresponding envelopes of higher force components for an incident wave group with the same peak period and an arbitrary amplitude by multiplying the scaling factor
![]() $s$
raised to the power
$s$
raised to the power
![]() $n$
due to the assumption that there is a generalized Stoke-type perturbation expansion for a wave group. The scaling factor
$n$
due to the assumption that there is a generalized Stoke-type perturbation expansion for a wave group. The scaling factor
![]() $s$
is set by the ratio of the maximum values of the linearized wave elevation envelope in the two cases being compared. Thus
$s$
is set by the ratio of the maximum values of the linearized wave elevation envelope in the two cases being compared. Thus
![]() $s^{n}$
becomes a direct check on the Stokes-like amplitude scalings of the two cases. The idea of amplitude scaling is investigated in figure 9. A direct comparison between the harmonic plots in the figure 9(a,b) is made by scaling the vertical axis by
$s^{n}$
becomes a direct check on the Stokes-like amplitude scalings of the two cases. The idea of amplitude scaling is investigated in figure 9. A direct comparison between the harmonic plots in the figure 9(a,b) is made by scaling the vertical axis by
![]() $s^{n}$
for the
$s^{n}$
for the
![]() $n$
th-order harmonic. The ratio of the peaks of the envelopes for the linear force components between figure 9(a,b) is 1.74, consistent with the ratio in peak linear amplitudes of surface elevation for the two incident wave groups. The scaling coefficient for each harmonic(s) is shown on the right of each plot in figure 9(a). It can be seen from the pairs of figures for each harmonic that the Stokes scaling applies quite well for all the nonlinear harmonics. The slightly increased differences in amplitude at fourth- and fifth-order harmonic are expected, as the effect of any slight error due to misalignment increases with each harmonic.
$n$
th-order harmonic. The ratio of the peaks of the envelopes for the linear force components between figure 9(a,b) is 1.74, consistent with the ratio in peak linear amplitudes of surface elevation for the two incident wave groups. The scaling coefficient for each harmonic(s) is shown on the right of each plot in figure 9(a). It can be seen from the pairs of figures for each harmonic that the Stokes scaling applies quite well for all the nonlinear harmonics. The slightly increased differences in amplitude at fourth- and fifth-order harmonic are expected, as the effect of any slight error due to misalignment increases with each harmonic.
Figure 10 shows the equivalent results for a pair of bidirectional cases with different amplitudes (
![]() $A_{f}=0.094~\text{m}$
,
$A_{f}=0.094~\text{m}$
,
![]() $k_{f}A_{f}=0.19$
) and (
$k_{f}A_{f}=0.19$
) and (
![]() $A_{f}=0.126~\text{m}$
,
$A_{f}=0.126~\text{m}$
,
![]() $k_{f}A_{f}=0.248$
). Each of the two component groups used to produce the bidirectional waves shown in figure 10 is the same as those shown in figure 9. It can be seen that the applied two-phase separation technique works quite well even for the violent bidirectional harmonic group.
$k_{f}A_{f}=0.248$
). Each of the two component groups used to produce the bidirectional waves shown in figure 10 is the same as those shown in figure 9. It can be seen that the applied two-phase separation technique works quite well even for the violent bidirectional harmonic group.

Figure 10. The harmonic structures of horizontal wave loading on the cylinder and the envelopes for bidirectional focused wave groups propagating in a flat bed. The peak frequency
![]() $f_{p}=0.61~\text{Hz}$
. (a) Bidirectional case with each component corresponding to the case shown in figure 9(a) with
$f_{p}=0.61~\text{Hz}$
. (a) Bidirectional case with each component corresponding to the case shown in figure 9(a) with
![]() $A_{f}=0.094~\text{m}$
(
$A_{f}=0.094~\text{m}$
(
![]() $k_{f}A_{f}=0.19$
), (b) bidirectional case with each component corresponding to the case shown in figure 9(b) with
$k_{f}A_{f}=0.19$
), (b) bidirectional case with each component corresponding to the case shown in figure 9(b) with
![]() $A_{f}=0.126~\text{m}$
(
$A_{f}=0.126~\text{m}$
(
![]() $k_{f}A_{f}=0.248$
).
$k_{f}A_{f}=0.248$
).
A sloping 1-in-20 bed was also installed in the tank. Figure 11(a) shows results of a unidirectional wave group with actual linearized peak amplitude
![]() $A_{f}=0.064~\text{m}$
(
$A_{f}=0.064~\text{m}$
(
![]() $k_{f}A_{f}=0.125$
) and figure 11(b) is a unidirectional wave group with larger amplitude
$k_{f}A_{f}=0.125$
) and figure 11(b) is a unidirectional wave group with larger amplitude
![]() $A_{f}=0.102~\text{m}$
(
$A_{f}=0.102~\text{m}$
(
![]() $k_{f}A_{f}=0.201$
), both with peak frequency of 0.61 Hz. These are similar wave groups to those shown in figure 9 except for the change in the tank geometry to the sloping rather than flat bed. As in figure 9, the axes in figure 11(b) are all scaled by the scaling factor to the appropriate power to allow comparison between those two wave groups that have the same peak frequency but different wave amplitude. The scaling factor is 1.73 for the sloping bed case. Except for the third harmonic of the force the two figures are still comparable, with close matching in wave shapes and sizes of each harmonic, which indicates that the Stokes-type perturbation expansion also applies even in the cases with a sloping bed.
$k_{f}A_{f}=0.201$
), both with peak frequency of 0.61 Hz. These are similar wave groups to those shown in figure 9 except for the change in the tank geometry to the sloping rather than flat bed. As in figure 9, the axes in figure 11(b) are all scaled by the scaling factor to the appropriate power to allow comparison between those two wave groups that have the same peak frequency but different wave amplitude. The scaling factor is 1.73 for the sloping bed case. Except for the third harmonic of the force the two figures are still comparable, with close matching in wave shapes and sizes of each harmonic, which indicates that the Stokes-type perturbation expansion also applies even in the cases with a sloping bed.
Thus, we have demonstrated that for each nonlinear
![]() $n$
th harmonic for force, the envelope
$n$
th harmonic for force, the envelope
![]() ${\sim}$
(shape of linear component envelope)
${\sim}$
(shape of linear component envelope)
![]() $^{n}\times (A_{f}/R)^{n}$
. So, the envelope shapes and magnitudes of each harmonic are consistent with a Stokes-type perturbation expansion. We now go further and examine the time history of the
$^{n}\times (A_{f}/R)^{n}$
. So, the envelope shapes and magnitudes of each harmonic are consistent with a Stokes-type perturbation expansion. We now go further and examine the time history of the
![]() $n$
th force harmonic. Using the narrow-band approximation outlined in (3.6) generalized to all the sum harmonics, we attempt to reconstruct the complete time history of each harmonic using only the linear component, an amplitude coefficient and a phase angle at each harmonic, as shown in figure 12. Generally this works well for all cases; figure 12 is typical. But again we note that such a reconstruction works least well for the third harmonic in each case.
$n$
th force harmonic. Using the narrow-band approximation outlined in (3.6) generalized to all the sum harmonics, we attempt to reconstruct the complete time history of each harmonic using only the linear component, an amplitude coefficient and a phase angle at each harmonic, as shown in figure 12. Generally this works well for all cases; figure 12 is typical. But again we note that such a reconstruction works least well for the third harmonic in each case.
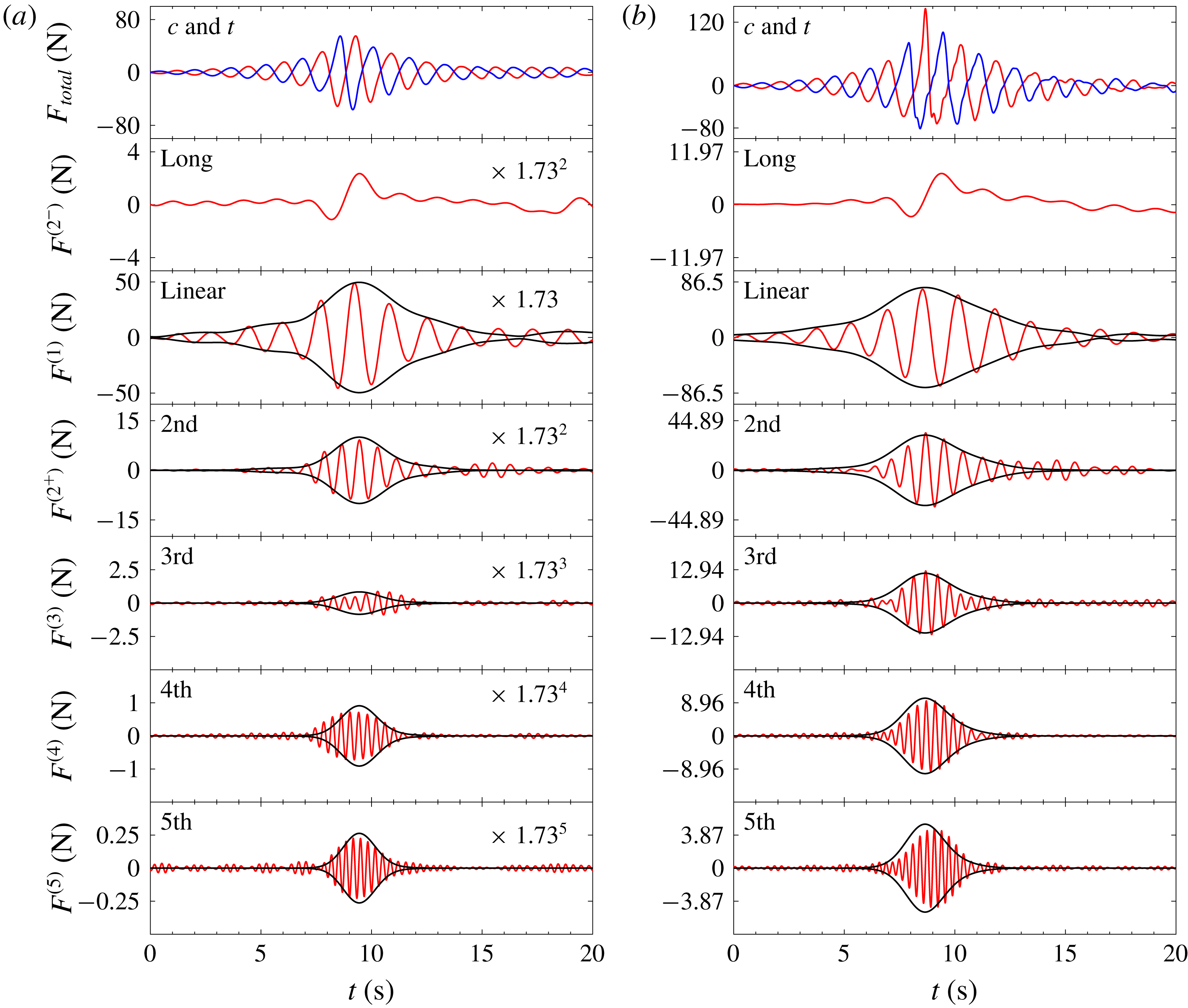
Figure 11. The harmonic structures of horizontal wave loading on the cylinder and the envelopes for both focused wave groups with
![]() $A_{f}=0.064~\text{m}$
and 0.102 m propagating up a sloping bed. The peak frequency
$A_{f}=0.064~\text{m}$
and 0.102 m propagating up a sloping bed. The peak frequency
![]() $f_{p}=0.61~\text{Hz}$
. (a) Unidirectional:
$f_{p}=0.61~\text{Hz}$
. (a) Unidirectional:
![]() $A_{f}=0.064~\text{m}$
(
$A_{f}=0.064~\text{m}$
(
![]() $k_{f}A_{f}=0.125$
), (b) unidirectional:
$k_{f}A_{f}=0.125$
), (b) unidirectional:
![]() $A_{f}=0.102~\text{m}$
(
$A_{f}=0.102~\text{m}$
(
![]() $k_{f}A_{f}=0.201$
).
$k_{f}A_{f}=0.201$
).

Figure 12. The reconstruction of horizontal wave loading on the cylinder for both focused wave groups shown in figure 11, the peak frequency
![]() $f_{p}=0.61~\text{Hz}$
. (a) For focused wave groups shown in figure 11(a) with
$f_{p}=0.61~\text{Hz}$
. (a) For focused wave groups shown in figure 11(a) with
![]() $A_{f}=0.064~\text{m}$
(
$A_{f}=0.064~\text{m}$
(
![]() $k_{f}A_{f}=0.125$
), (b) for focused wave groups shown in figure 11(b) with
$k_{f}A_{f}=0.125$
), (b) for focused wave groups shown in figure 11(b) with
![]() $A_{f}=0.102~\text{m}$
(
$A_{f}=0.102~\text{m}$
(
![]() $k_{f}A_{f}=0.201$
).
$k_{f}A_{f}=0.201$
).
6 Sloping bed versus flat bed
It is worth noting that the water depths for the sloping and flat bed tests were same at the centre of the cylinder on which the force measurements were measured rather than at the wave paddle. The water depths at the wave paddle for the sloping and flat bed tests were 0.8 m and 0.505 m, respectively. It is important to investigate the variation of the wave loading with the local wave steepness at the centre of the cylinder, which is also the intended focal point for the incident wave groups. The measured free-surface time series from wave gauge WG9 for cases without the cylinder in place are used to obtain the peak of the linear envelope. The wavenumber at the centre of the cylinder is calculated with the local water depth
![]() $d=0.505~\text{m}$
, as discussed in § 2. The resulting wave steepness at the centre of the cylinder
$d=0.505~\text{m}$
, as discussed in § 2. The resulting wave steepness at the centre of the cylinder
![]() $k_{f}A_{f}$
are shown in table 1.
$k_{f}A_{f}$
are shown in table 1.
Figure 13 shows the variation of the total peak wave loading on the cylinder with the wave steepness
![]() $k_{f}A_{f}$
at the focal point for both the sloping and flat bed cases. It can be seen that the total peak force on the cylinder increases with the wave steepness at the focal point for both sloping and flat bed cases, and the focused wave groups with smaller wave peak spectral frequency and longer wavelength lead to larger wave loading on the cylinder for both sloping and flat bed cases. There are only three to five points (symbols) per line in figure 13, but the trends appear robust. Remarkably the results for the sloping bed and flat bed tests now agree well, which indicates that the wave loading on the cylinder depends strongly on the local water depth at the cylinder and not significantly on the local bed slope. The slight discrepancy for the longest waves with
$k_{f}A_{f}$
at the focal point for both the sloping and flat bed cases. It can be seen that the total peak force on the cylinder increases with the wave steepness at the focal point for both sloping and flat bed cases, and the focused wave groups with smaller wave peak spectral frequency and longer wavelength lead to larger wave loading on the cylinder for both sloping and flat bed cases. There are only three to five points (symbols) per line in figure 13, but the trends appear robust. Remarkably the results for the sloping bed and flat bed tests now agree well, which indicates that the wave loading on the cylinder depends strongly on the local water depth at the cylinder and not significantly on the local bed slope. The slight discrepancy for the longest waves with
![]() $f_{p}=0.49~\text{Hz}$
probably occurs because the focusing is being affected by nonlinearity differently for the two bed geometries. It should be noted that the independence of bed slope is demonstrated for the 1-in-20 slope. Many sites where offshore wind turbines are located have bed slopes smaller than this.
$f_{p}=0.49~\text{Hz}$
probably occurs because the focusing is being affected by nonlinearity differently for the two bed geometries. It should be noted that the independence of bed slope is demonstrated for the 1-in-20 slope. Many sites where offshore wind turbines are located have bed slopes smaller than this.

Figure 13. Variation of the total peak wave loading on the cylinder with the wave steepness
![]() $k_{f}A_{f}$
. Filled symbols represent the results for the sloping bed cases and open symbols represent the results for the flat bed cases.
$k_{f}A_{f}$
. Filled symbols represent the results for the sloping bed cases and open symbols represent the results for the flat bed cases.
The relative contributions of the higher-order harmonics up to fourth order are investigated in figure 14. A log-scale is used on the vertical axis to show the low level of third- and fourth-order harmonic forces. It can be seen that the linear force component always dominates the higher-order harmonic forces, although its relative value decreases with the increasing wave steepness. The higher-order harmonic forces increase with the increasing wave steepness and are of significant size when the amplitude
![]() $A_{f}$
is increased up to the radius of the cylinder
$A_{f}$
is increased up to the radius of the cylinder
![]() $R(=0.125~\text{m})$
, i.e.
$R(=0.125~\text{m})$
, i.e.
![]() $k_{f}A_{f}\sim k_{f}R$
. The linear force component on the cylinder can be less than half of the total force, as seen in figure 14(a). It is clear that conventional linear or even second-order diffraction analysis for an extreme case could lead to a significant underestimation in the total wave loading. Additionally, it can be demonstrated that the contributions of the higher-order harmonic forces decrease with the increasing cylinder size
$k_{f}A_{f}\sim k_{f}R$
. The linear force component on the cylinder can be less than half of the total force, as seen in figure 14(a). It is clear that conventional linear or even second-order diffraction analysis for an extreme case could lead to a significant underestimation in the total wave loading. Additionally, it can be demonstrated that the contributions of the higher-order harmonic forces decrease with the increasing cylinder size
![]() $k_{f}R$
for a fixed wave steepness. From figure 14(a), the maximum contributions of the nonlinear wave force components higher than the linear component are approximately 60 %, 50 %, 30 % and 10 % of the total force for
$k_{f}R$
for a fixed wave steepness. From figure 14(a), the maximum contributions of the nonlinear wave force components higher than the linear component are approximately 60 %, 50 %, 30 % and 10 % of the total force for
![]() $k_{f}R=0.188$
, 0.246, 0.373 and 0.753, respectively. As might be anticipated, the reasonably good agreement between the results of sloping and flat bed tests confirms that the relative contribution of the various harmonics to the total force is only related to the wave parameters measured at the centre of the cylinder rather than at the wave paddle, i.e. by analogy, locally rather than further offshore in deeper water.
$k_{f}R=0.188$
, 0.246, 0.373 and 0.753, respectively. As might be anticipated, the reasonably good agreement between the results of sloping and flat bed tests confirms that the relative contribution of the various harmonics to the total force is only related to the wave parameters measured at the centre of the cylinder rather than at the wave paddle, i.e. by analogy, locally rather than further offshore in deeper water.

Figure 14. Variation of extracted harmonics with the wave steepness
![]() $k_{f}A_{f}$
. (a) Linear force component, (b) second-harmonic forces, (c) third-harmonic forces, (d) fourth-harmonic forces. Solid symbols with solid lines for sloping bed and open symbols for flat bed. Circular red markers:
$k_{f}A_{f}$
. (a) Linear force component, (b) second-harmonic forces, (c) third-harmonic forces, (d) fourth-harmonic forces. Solid symbols with solid lines for sloping bed and open symbols for flat bed. Circular red markers:
![]() $k_{f}R=0.188$
; square blue markers:
$k_{f}R=0.188$
; square blue markers:
![]() $k_{f}R=0.246$
; diamond green markers:
$k_{f}R=0.246$
; diamond green markers:
![]() $k_{f}R=0.373$
; triangular black markers:
$k_{f}R=0.373$
; triangular black markers:
![]() $k_{f}R=0.753$
.
$k_{f}R=0.753$
.
7 The Huseby and Grue scalings for force components
7.1 Harmonic structure of forces
Using the scaling introduced by Huseby & Grue (Reference Huseby and Grue2000), the amplitude of the
![]() $n$
th-harmonic force is now non-dimensionalized by dividing by
$n$
th-harmonic force is now non-dimensionalized by dividing by
![]() $\unicode[STIX]{x1D70C}gA_{f}^{n}R^{(3-n)}$
, where
$\unicode[STIX]{x1D70C}gA_{f}^{n}R^{(3-n)}$
, where
![]() $A_{f}$
is the maximum value of the linearized wave elevation envelope at the position of the cylinder. Figure 15 shows the results for the linear force component for wave steepness up to 0.3. The results for both the sloping and flat bed cases are included. The inertia term in the Morison equation is applied to obtain an estimation of the linear force component. In the present experiments
$A_{f}$
is the maximum value of the linearized wave elevation envelope at the position of the cylinder. Figure 15 shows the results for the linear force component for wave steepness up to 0.3. The results for both the sloping and flat bed cases are included. The inertia term in the Morison equation is applied to obtain an estimation of the linear force component. In the present experiments
![]() $0.3<KC<3$
for the unidirectional focused wave, and the ratio
$0.3<KC<3$
for the unidirectional focused wave, and the ratio
![]() $Re/KC$
is larger than 31 000, for the large waves, where
$Re/KC$
is larger than 31 000, for the large waves, where
![]() $KC$
and
$KC$
and
![]() $Re$
are the Keulegan Carpenter and Reynolds numbers, respectively. Sarpkaya (Reference Sarpkaya1986, figure 3) and Huseby & Grue (Reference Huseby and Grue2000) show that the viscous drag force on a circular cylinder is relatively small for these values of
$Re$
are the Keulegan Carpenter and Reynolds numbers, respectively. Sarpkaya (Reference Sarpkaya1986, figure 3) and Huseby & Grue (Reference Huseby and Grue2000) show that the viscous drag force on a circular cylinder is relatively small for these values of
![]() $KC$
and
$KC$
and
![]() $Re$
. The inertia coefficient expected for most of these tests is 2, which is the standard value for uniform flow normal to the cylinder axis. The Morison term hereafter implies the inertia contribution from the Morison equation, unless otherwise stated. A frequency domain potential-flow solver DIFFRACT has also been applied to obtain first- and second-order harmonic wave loading on the cylinder that is located on the flat seabed (Eatock Taylor & Chau Reference Eatock Taylor and Chau1992; Zang et al.
Reference Zang, Gibson, Taylor, Eatock Taylor and Swan2006).
$Re$
. The inertia coefficient expected for most of these tests is 2, which is the standard value for uniform flow normal to the cylinder axis. The Morison term hereafter implies the inertia contribution from the Morison equation, unless otherwise stated. A frequency domain potential-flow solver DIFFRACT has also been applied to obtain first- and second-order harmonic wave loading on the cylinder that is located on the flat seabed (Eatock Taylor & Chau Reference Eatock Taylor and Chau1992; Zang et al.
Reference Zang, Gibson, Taylor, Eatock Taylor and Swan2006).
It can be seen that for all four cylinder sizes investigated, the non-dimensional linear force component is approximately constant for the whole range of wave steepnesses, even when the wave steepness
![]() $k_{f}A_{f}$
become quite large. Our measurements agree well with the Morison linear inertia force and the potential-flow solutions from DIFFRACT. For the largest cylinder (
$k_{f}A_{f}$
become quite large. Our measurements agree well with the Morison linear inertia force and the potential-flow solutions from DIFFRACT. For the largest cylinder (
![]() $k_{f}R=0.753$
), the result is beyond the expected range of validity of the Morison equation. A similar observation has been made by Huseby & Grue (Reference Huseby and Grue2000) in their experiments, in which the incoming waves were Stokes waves with wave slope up to 0.24, and the maximum non-dimensional cylinder size was 0.378. In Huseby & Grue (Reference Huseby and Grue2000) deep water waves were considered; thus, the effect of water depth is limited.
$k_{f}R=0.753$
), the result is beyond the expected range of validity of the Morison equation. A similar observation has been made by Huseby & Grue (Reference Huseby and Grue2000) in their experiments, in which the incoming waves were Stokes waves with wave slope up to 0.24, and the maximum non-dimensional cylinder size was 0.378. In Huseby & Grue (Reference Huseby and Grue2000) deep water waves were considered; thus, the effect of water depth is limited.

Figure 15. Variation of the linear force component with wave steepness
![]() $k_{f}A_{f}$
. The linear force component is made non-dimensional using
$k_{f}A_{f}$
. The linear force component is made non-dimensional using
![]() $\unicode[STIX]{x1D70C}gA_{f}R^{2}$
. Solid lines from DIFFRACT, dashed lines from Morison inertia forces. Dot-dashed line from experiments by Huseby & Grue (Reference Huseby and Grue2000) with
$\unicode[STIX]{x1D70C}gA_{f}R^{2}$
. Solid lines from DIFFRACT, dashed lines from Morison inertia forces. Dot-dashed line from experiments by Huseby & Grue (Reference Huseby and Grue2000) with
![]() $k_{f}R=0.245$
. Solid symbols for sloping bed and open symbols for flat bed. Circular red markers:
$k_{f}R=0.245$
. Solid symbols for sloping bed and open symbols for flat bed. Circular red markers:
![]() $k_{f}R=0.188$
; square blue markers:
$k_{f}R=0.188$
; square blue markers:
![]() $k_{f}R=0.246$
; Diamond green markers:
$k_{f}R=0.246$
; Diamond green markers:
![]() $k_{f}R=0.373$
; triangular black markers:
$k_{f}R=0.373$
; triangular black markers:
![]() $k_{f}R=0.753$
.
$k_{f}R=0.753$
.
Similar analysis has been done for the double-frequency (second-order) harmonic force, and the results are shown in figure 16. It is clear that, when expressed in the manner proposed by Huseby & Grue (Reference Huseby and Grue2000), the non-dimensional second-order harmonic force is approximately constant across the entire variation of the wave steepness at the focal point, and decreases with increasing cylinder size
![]() $k_{f}R$
, i.e. with increasing wavenumber (decreasing wavelength) because the radius of the cylinder was kept fixed in all the experiments. The focused wave groups in sloping bed cases are close to breaking for
$k_{f}R$
, i.e. with increasing wavenumber (decreasing wavelength) because the radius of the cylinder was kept fixed in all the experiments. The focused wave groups in sloping bed cases are close to breaking for
![]() $k_{f}A_{f}>0.2$
, so the idea of a smoothly varying envelope is somewhat suspect; hence the structure of the cylinder forces may be rather different. This may explain the relatively large increases for
$k_{f}A_{f}>0.2$
, so the idea of a smoothly varying envelope is somewhat suspect; hence the structure of the cylinder forces may be rather different. This may explain the relatively large increases for
![]() $k_{f}A_{f}>0.2$
at
$k_{f}A_{f}>0.2$
at
![]() $k_{f}R=0.246$
and 0.373. In Huseby & Grue (Reference Huseby and Grue2000) a similar observation was made, though the second-order harmonic force decreases with the wavenumber slightly (dot-dashed line in figure 16). These trends in the first- and second-order harmonic forces are applicable to both the sloping and flat bed tests, and the effect of the bed slope appears small. The magnitudes of the second-order force harmonic in this study are larger than those in Huseby & Grue (Reference Huseby and Grue2000) due to the larger nonlinearity for shallow water waves.
$k_{f}R=0.246$
and 0.373. In Huseby & Grue (Reference Huseby and Grue2000) a similar observation was made, though the second-order harmonic force decreases with the wavenumber slightly (dot-dashed line in figure 16). These trends in the first- and second-order harmonic forces are applicable to both the sloping and flat bed tests, and the effect of the bed slope appears small. The magnitudes of the second-order force harmonic in this study are larger than those in Huseby & Grue (Reference Huseby and Grue2000) due to the larger nonlinearity for shallow water waves.
The phase of the second-order harmonic force relative to the linear force component is shown in figure 17. It can be seen that for all but the largest cylinder (
![]() $k_{f}R=0.753$
), the phases of the second-order harmonic force are quite constant as the wave steepness increases up to 0.2, and then decrease with further increase in wave steepness. Huseby & Grue (Reference Huseby and Grue2000) also found in their experiments that the phases of second-order harmonic force are approximately constant when the wave steepness is smaller than
$k_{f}R=0.753$
), the phases of the second-order harmonic force are quite constant as the wave steepness increases up to 0.2, and then decrease with further increase in wave steepness. Huseby & Grue (Reference Huseby and Grue2000) also found in their experiments that the phases of second-order harmonic force are approximately constant when the wave steepness is smaller than
![]() ${\sim}0.2$
, though the phase of the
${\sim}0.2$
, though the phase of the
![]() $n$
th-order harmonic force was defined as the phase difference relative to the incoming waves rather than the linear force component. An opposing trend is observed for the largest cylinder (
$n$
th-order harmonic force was defined as the phase difference relative to the incoming waves rather than the linear force component. An opposing trend is observed for the largest cylinder (
![]() $k_{f}R=0.753$
). The phases increase with the wave steepness after 0.2. The NewWave envelope for the steeper waves from a higher-frequency wave group (
$k_{f}R=0.753$
). The phases increase with the wave steepness after 0.2. The NewWave envelope for the steeper waves from a higher-frequency wave group (
![]() $f_{p}=1.22~\text{Hz}$
,
$f_{p}=1.22~\text{Hz}$
,
![]() $k_{f}A_{f}=0.247$
) is no longer symmetric due to third-order wave–wave interactions and strong nonlinearity (Adcock & Taylor Reference Adcock and Taylor2009). The envelope has a very steep rise and a slow decay, as shown in figure 18. This might lead to different behaviour of the wave groups with higher frequency and larger wave steepness. But again, there is good agreement between the sloping and flat bed results.
$k_{f}A_{f}=0.247$
) is no longer symmetric due to third-order wave–wave interactions and strong nonlinearity (Adcock & Taylor Reference Adcock and Taylor2009). The envelope has a very steep rise and a slow decay, as shown in figure 18. This might lead to different behaviour of the wave groups with higher frequency and larger wave steepness. But again, there is good agreement between the sloping and flat bed results.

Figure 16. Variation of second-order harmonic forces with wave steepness
![]() $k_{f}A_{f}$
. The second-order harmonic forces are made non-dimensional using
$k_{f}A_{f}$
. The second-order harmonic forces are made non-dimensional using
![]() $\unicode[STIX]{x1D70C}gA_{f}^{2}R$
. Solid lines from DIFFRACT. Dot-dashed line from experiments by Huseby & Grue (Reference Huseby and Grue2000) with
$\unicode[STIX]{x1D70C}gA_{f}^{2}R$
. Solid lines from DIFFRACT. Dot-dashed line from experiments by Huseby & Grue (Reference Huseby and Grue2000) with
![]() $k_{f}R=0.245$
. Solid symbols for sloping bed and open symbols for the flat bed. Circular red markers:
$k_{f}R=0.245$
. Solid symbols for sloping bed and open symbols for the flat bed. Circular red markers:
![]() $k_{f}R=0.188$
; square blue markers:
$k_{f}R=0.188$
; square blue markers:
![]() $k_{f}R=0.246$
; diamond green markers:
$k_{f}R=0.246$
; diamond green markers:
![]() $k_{f}R=0.373$
; triangular black markers:
$k_{f}R=0.373$
; triangular black markers:
![]() $k_{f}R=0.753$
.
$k_{f}R=0.753$
.

Figure 17. Variation of phase of second-order force harmonics with wave steepness
![]() $k_{f}A_{f}$
. Solid symbols with solid line for sloping bed and open symbols for the flat bed. Circular red markers:
$k_{f}A_{f}$
. Solid symbols with solid line for sloping bed and open symbols for the flat bed. Circular red markers:
![]() $k_{f}R=0.188$
; square blue markers:
$k_{f}R=0.188$
; square blue markers:
![]() $k_{f}R=0.246$
; diamond green markers:
$k_{f}R=0.246$
; diamond green markers:
![]() $k_{f}R=0.373$
; triangular black markers:
$k_{f}R=0.373$
; triangular black markers:
![]() $k_{f}R=0.753$
.
$k_{f}R=0.753$
.

Figure 18. Force–time history for the wave group with
![]() $A_{f}=0.041~\text{m}$
propagating in a flat bed. The peak frequency
$A_{f}=0.041~\text{m}$
propagating in a flat bed. The peak frequency
![]() $f_{p}=1.22~\text{Hz}$
.
$f_{p}=1.22~\text{Hz}$
.
![]() $k_{f}A_{f}=0.246$
.
$k_{f}A_{f}=0.246$
.
Variation of non-dimensional first- and second-order force harmonics with the cylinder size
![]() $k_{f}R$
are also shown in figure 19. The experimental data is compared to the Morison compact linear inertia term as well as the classical diffraction and the MacCamy–Fuchs solutions (MacCamy & Fuchs Reference MacCamy and Fuchs1954). The experimental data in figure 19 are shown by the mean values across wave steepness from figure 15 and figure 16, using the same symbols to indicate both cylinder size (
$k_{f}R$
are also shown in figure 19. The experimental data is compared to the Morison compact linear inertia term as well as the classical diffraction and the MacCamy–Fuchs solutions (MacCamy & Fuchs Reference MacCamy and Fuchs1954). The experimental data in figure 19 are shown by the mean values across wave steepness from figure 15 and figure 16, using the same symbols to indicate both cylinder size (
![]() $k_{f}R$
) and bed geometry, flat or sloping. The error bars on the left-hand side of the each symbol represents the variability of the harmonic force for flat bed tests and those on the right-hand side are for sloping bed tests. Generally, the non-dimensional linear force component increases with increasing cylinder size up to a certain point and then decreases with further increasing cylinder size. The Morison term predicts the linear force quite well for a smaller cylinder size (
$k_{f}R$
) and bed geometry, flat or sloping. The error bars on the left-hand side of the each symbol represents the variability of the harmonic force for flat bed tests and those on the right-hand side are for sloping bed tests. Generally, the non-dimensional linear force component increases with increasing cylinder size up to a certain point and then decreases with further increasing cylinder size. The Morison term predicts the linear force quite well for a smaller cylinder size (
![]() $k_{f}R\sim (0{-}0.4)$
) while failing to give a good approximation for larger cylinders. The numerical classical diffraction results and the MacCamy–Fuchs equation match and give good estimations of the first-harmonic forces for all four cylinder sizes considered. It also can be seen that the non-dimensional second-order harmonic force rapidly decreases with increasing cylinder size to a minimum at a non-dimensional size of
$k_{f}R\sim (0{-}0.4)$
) while failing to give a good approximation for larger cylinders. The numerical classical diffraction results and the MacCamy–Fuchs equation match and give good estimations of the first-harmonic forces for all four cylinder sizes considered. It also can be seen that the non-dimensional second-order harmonic force rapidly decreases with increasing cylinder size to a minimum at a non-dimensional size of
![]() ${\sim}0.5$
, and that the size of the second-order term is the same for a cylinder twice as large (
${\sim}0.5$
, and that the size of the second-order term is the same for a cylinder twice as large (
![]() $k_{f}R=0.753$
) due to strong diffraction effects. Good agreement is achieved between the experimental data and the second-order diffraction solutions, indicating that classical diffraction theory is applicable for the wave and loading conditions investigated in this work.
$k_{f}R=0.753$
) due to strong diffraction effects. Good agreement is achieved between the experimental data and the second-order diffraction solutions, indicating that classical diffraction theory is applicable for the wave and loading conditions investigated in this work.

Figure 19. Variation of non-dimensional first- and second-order force harmonics with the cylinder size
![]() $k_{f}R$
. (a) First-order force harmonic; (b) second-order force harmonic.
$k_{f}R$
. (a) First-order force harmonic; (b) second-order force harmonic.
The results for the third-, fourth- and fifth-order harmonic forces are shown in figures 20–22, respectively. The experimental results of Huseby & Grue (Reference Huseby and Grue2000) are also included for comparison. We note that the magnitudes of the third- and higher-order harmonic forces are small, below the noise level, for smaller wave steepness for all four cylinder sizes. For example, the third- and fourth-order harmonic forces are smaller than 5 % and 1 % of the total forces when
![]() $k_{f}A_{f}<0.1$
, as shown in figure 14(c,d). And recalling that steeper waves with higher wave frequency (
$k_{f}A_{f}<0.1$
, as shown in figure 14(c,d). And recalling that steeper waves with higher wave frequency (
![]() $k_{f}R=0.753$
) are susceptible to nonlinear effects, it is reasonable to have some experimental scatter in the results shown in figures 20–22. Kristiansen & Faltinsen (Reference Kristiansen and Faltinsen2017) observed a distinct run-up at the rear of the cylinder above a limiting wave steepness of approximately
$k_{f}R=0.753$
) are susceptible to nonlinear effects, it is reasonable to have some experimental scatter in the results shown in figures 20–22. Kristiansen & Faltinsen (Reference Kristiansen and Faltinsen2017) observed a distinct run-up at the rear of the cylinder above a limiting wave steepness of approximately
![]() $H/\unicode[STIX]{x1D706}=1/40$
(
$H/\unicode[STIX]{x1D706}=1/40$
(
![]() $kA=0.08$
) in finite water depth. They speculated that this run-up results from a viscous flow separation using an ideal section-wise two-dimensional CFD model. This may also explain the slightly different trend/scatter in higher harmonics at larger wave steepness in this study. Additionally, if the error in the measured wave elevation is
$kA=0.08$
) in finite water depth. They speculated that this run-up results from a viscous flow separation using an ideal section-wise two-dimensional CFD model. This may also explain the slightly different trend/scatter in higher harmonics at larger wave steepness in this study. Additionally, if the error in the measured wave elevation is
![]() $e$
, which is approximately 2 % typically, then relative error of
$e$
, which is approximately 2 % typically, then relative error of
![]() $ne$
would be introduced in the amplitude of the non-dimensional
$ne$
would be introduced in the amplitude of the non-dimensional
![]() $n$
th-order harmonic force based on the current scaling analysis (Huseby & Grue Reference Huseby and Grue2000). Given the increasing error and the small size of the higher force harmonics, the agreement between the sloping and flat bed tests is still reasonable, as shown in figures 20–22. After allowing for the inherent variability, it is also clear that the higher force harmonics still show Stokes-like scaling, with no systematic variation with wave steepness beyond this.
$n$
th-order harmonic force based on the current scaling analysis (Huseby & Grue Reference Huseby and Grue2000). Given the increasing error and the small size of the higher force harmonics, the agreement between the sloping and flat bed tests is still reasonable, as shown in figures 20–22. After allowing for the inherent variability, it is also clear that the higher force harmonics still show Stokes-like scaling, with no systematic variation with wave steepness beyond this.

Figure 20. Variation of third-order harmonic forces with wave steepness
![]() $k_{f}A_{f}$
. The third-order harmonic forces are made non-dimensional using
$k_{f}A_{f}$
. The third-order harmonic forces are made non-dimensional using
![]() $\unicode[STIX]{x1D70C}gA_{f}^{3}$
. Dot-dashed line from experiments by Huseby & Grue (Reference Huseby and Grue2000), blue for
$\unicode[STIX]{x1D70C}gA_{f}^{3}$
. Dot-dashed line from experiments by Huseby & Grue (Reference Huseby and Grue2000), blue for
![]() $k_{f}R=0.245$
, green for
$k_{f}R=0.245$
, green for
![]() $0.378$
; dashed line is the FNV solution, bottom to top:
$0.378$
; dashed line is the FNV solution, bottom to top:
![]() $k_{f}R=0.188$
, 0.246, 0.373 and 0.753. Solid symbols for sloping bed and open symbols for flat bed. Circular red markers:
$k_{f}R=0.188$
, 0.246, 0.373 and 0.753. Solid symbols for sloping bed and open symbols for flat bed. Circular red markers:
![]() $k_{f}R=0.188$
; square blue markers:
$k_{f}R=0.188$
; square blue markers:
![]() $k_{f}R=0.246$
; diamond green markers:
$k_{f}R=0.246$
; diamond green markers:
![]() $k_{f}R=0.373$
; triangle black markers:
$k_{f}R=0.373$
; triangle black markers:
![]() $k_{f}R=0.753$
.
$k_{f}R=0.753$
.

Figure 21. Variation of fourth-order harmonic forces with wave steepness
![]() $k_{f}A_{f}$
. The fourth-order harmonic forces are made non-dimensional using
$k_{f}A_{f}$
. The fourth-order harmonic forces are made non-dimensional using
![]() $\unicode[STIX]{x1D70C}gA_{f}^{4}R^{-1}$
. Dot-dashed line from experiments by Huseby & Grue (Reference Huseby and Grue2000), blue for
$\unicode[STIX]{x1D70C}gA_{f}^{4}R^{-1}$
. Dot-dashed line from experiments by Huseby & Grue (Reference Huseby and Grue2000), blue for
![]() $k_{f}R=0.245$
, green for
$k_{f}R=0.245$
, green for
![]() $0.378$
. Solid symbols for sloping bed and open symbols for flat bed. Circular red markers:
$0.378$
. Solid symbols for sloping bed and open symbols for flat bed. Circular red markers:
![]() $k_{f}R=0.188$
; square blue markers:
$k_{f}R=0.188$
; square blue markers:
![]() $k_{f}R=0.246$
; diamond green markers:
$k_{f}R=0.246$
; diamond green markers:
![]() $k_{f}R=0.373$
; triangle black markers:
$k_{f}R=0.373$
; triangle black markers:
![]() $k_{f}R=0.753$
.
$k_{f}R=0.753$
.

Figure 22. Variation of fifth-order harmonic forces with wave steepness
![]() $k_{f}A_{f}$
. The fifth-order harmonic forces are made non-dimensional using
$k_{f}A_{f}$
. The fifth-order harmonic forces are made non-dimensional using
![]() $\unicode[STIX]{x1D70C}gA_{f}^{5}R^{-2}$
. Dot-dashed line from experiments by Huseby & Grue (Reference Huseby and Grue2000) with
$\unicode[STIX]{x1D70C}gA_{f}^{5}R^{-2}$
. Dot-dashed line from experiments by Huseby & Grue (Reference Huseby and Grue2000) with
![]() $k_{f}R=0.245$
. Solid symbols for sloping bed and open symbols for flat bed. Circular red markers:
$k_{f}R=0.245$
. Solid symbols for sloping bed and open symbols for flat bed. Circular red markers:
![]() $k_{f}R=0.188$
; square blue markers:
$k_{f}R=0.188$
; square blue markers:
![]() $k_{f}R=0.246$
; diamond green markers:
$k_{f}R=0.246$
; diamond green markers:
![]() $k_{f}R=0.373$
; triangle black markers:
$k_{f}R=0.373$
; triangle black markers:
![]() $k_{f}R=0.753$
.
$k_{f}R=0.753$
.
The measurements of the third-order harmonic forces are also compared to the FNV model developed by Faltinsen et al. (Reference Faltinsen, Newman and Vinje1995) in figure 20. It can be seen that the FNV solutions and the experimental results from Huseby & Grue (Reference Huseby and Grue2000) agree well with our measurements for smaller cylinder size (
![]() $k_{f}R\sim (0.2{-}0.4)$
). Both our measurements and the measurements of Huseby & Grue (Reference Huseby and Grue2000) show that the third-order harmonic force coefficient is nearly constant as the wave steepness is increased. The FNV model overestimates the amplitude of the third-order harmonic force for larger cylinders (
$k_{f}R\sim (0.2{-}0.4)$
). Both our measurements and the measurements of Huseby & Grue (Reference Huseby and Grue2000) show that the third-order harmonic force coefficient is nearly constant as the wave steepness is increased. The FNV model overestimates the amplitude of the third-order harmonic force for larger cylinders (
![]() $k_{f}R=0.753$
, black triangle in the figure). The smallest cylinder results (red circle in the figure) apparently vary strongly with wave steepness, and the FNV prediction is considerably smaller as the cylinder is in very shallow water (
$k_{f}R=0.753$
, black triangle in the figure). The smallest cylinder results (red circle in the figure) apparently vary strongly with wave steepness, and the FNV prediction is considerably smaller as the cylinder is in very shallow water (
![]() $k_{f}d_{f}=0.763$
). It is interesting to see that both our measurements and the results from Huseby & Grue (Reference Huseby and Grue2000) give a decreasing amplitude of the third-order harmonic force with increasing wave steepness up to 0.15 for the longest waves (
$k_{f}d_{f}=0.763$
). It is interesting to see that both our measurements and the results from Huseby & Grue (Reference Huseby and Grue2000) give a decreasing amplitude of the third-order harmonic force with increasing wave steepness up to 0.15 for the longest waves (
![]() $k_{f}R=0.188$
, red circle in the figure and figure 21 in Huseby & Grue (Reference Huseby and Grue2000)). An increase in the third-order harmonic force for the sloping bed tests is observed for
$k_{f}R=0.188$
, red circle in the figure and figure 21 in Huseby & Grue (Reference Huseby and Grue2000)). An increase in the third-order harmonic force for the sloping bed tests is observed for
![]() $k_{f}A>0.2$
, which may result from the observed run-up at the rear of the cylinder in finite water depth, as mentioned in Kristiansen & Faltinsen (Reference Kristiansen and Faltinsen2017). For the most slender cylinder cases (
$k_{f}A>0.2$
, which may result from the observed run-up at the rear of the cylinder in finite water depth, as mentioned in Kristiansen & Faltinsen (Reference Kristiansen and Faltinsen2017). For the most slender cylinder cases (
![]() $k_{f}R=0.188$
), these correspond to rather shallow water waves (
$k_{f}R=0.188$
), these correspond to rather shallow water waves (
![]() $k_{f}d_{f}=0.76$
). Here, we have some difficulty in achieving good time alignment for crest and trough focused cases. This is probably because the propagation speeds of large crests and troughs are slightly different (due to triad wave–wave interactions), so estimation of the coefficients of higher harmonics becomes more difficult.
$k_{f}d_{f}=0.76$
). Here, we have some difficulty in achieving good time alignment for crest and trough focused cases. This is probably because the propagation speeds of large crests and troughs are slightly different (due to triad wave–wave interactions), so estimation of the coefficients of higher harmonics becomes more difficult.
It can be seen from figures 21–22 that the fourth- and fifth-order harmonic force coefficients for the wave conditions investigated in this work roughly collapse on constant values of
![]() ${\sim}0.67$
and
${\sim}0.67$
and
![]() ${\sim}0.70$
, respectively, regardless the wave steepness and cylinder size. The large diameter cylinder results for
${\sim}0.70$
, respectively, regardless the wave steepness and cylinder size. The large diameter cylinder results for
![]() $k_{f}R=0.753$
are mostly larger and fit our analysis less well. This is different from what has been observed by Huseby & Grue (Reference Huseby and Grue2000), where the amplitude of the fourth-order harmonic force coefficient increases with the cylinder size
$k_{f}R=0.753$
are mostly larger and fit our analysis less well. This is different from what has been observed by Huseby & Grue (Reference Huseby and Grue2000), where the amplitude of the fourth-order harmonic force coefficient increases with the cylinder size
![]() $k_{f}R$
. Larger nonlinearity of shallow water waves in this study results in larger magnitudes of the fifth-order force harmonic when compared with Huseby & Grue (Reference Huseby and Grue2000).
$k_{f}R$
. Larger nonlinearity of shallow water waves in this study results in larger magnitudes of the fifth-order force harmonic when compared with Huseby & Grue (Reference Huseby and Grue2000).
The phases of the third-, fourth- and fifth-order harmonic forces are shown in figures 23–25, respectively. As expected, there is a reasonable match between the results of flat and sloping bed tests. As with the amplitude coefficients, the phases of the third-, fourth- and fifth-order harmonic forces, to a rough approximation, are constant for the whole range of wave steepness considered in this study.

Figure 23. Variation of the phases of the third-order harmonic forces with wave steepness
![]() $k_{f}A_{f}$
. Solid symbols for sloping bed and open symbols for flat bed. Circular red markers:
$k_{f}A_{f}$
. Solid symbols for sloping bed and open symbols for flat bed. Circular red markers:
![]() $k_{f}R=0.188$
; square blue markers:
$k_{f}R=0.188$
; square blue markers:
![]() $k_{f}R=0.246$
; diamond green markers:
$k_{f}R=0.246$
; diamond green markers:
![]() $k_{f}R=0.373$
; triangle black markers:
$k_{f}R=0.373$
; triangle black markers:
![]() $k_{f}R=0.753$
.
$k_{f}R=0.753$
.
The averaged coefficients across all experimental wave steepness above
![]() $kA\sim 0.05$
are summarized in the Appendix. These are obtained from figures 15–25. Generally, the results for smallest (
$kA\sim 0.05$
are summarized in the Appendix. These are obtained from figures 15–25. Generally, the results for smallest (
![]() $k_{f}R=0.188$
) and largest cylinders (
$k_{f}R=0.188$
) and largest cylinders (
![]() $k_{f}R=0.753$
) fit our analysis less well. The water depth for the smallest cylinder (
$k_{f}R=0.753$
) fit our analysis less well. The water depth for the smallest cylinder (
![]() $k_{f}R=0.188$
) is very shallow (
$k_{f}R=0.188$
) is very shallow (
![]() $k_{f}d_{f}=0.763$
) and the cylinder with
$k_{f}d_{f}=0.763$
) and the cylinder with
![]() $k_{f}R=0.753$
is too large, thus it is not a slender cylinder.
$k_{f}R=0.753$
is too large, thus it is not a slender cylinder.

Figure 24. Variation of the phases of the fourth-order harmonic forces with wave steepness
![]() $k_{f}A_{f}$
. Solid symbols for sloping bed and open symbols for flat bed. Circular red markers:
$k_{f}A_{f}$
. Solid symbols for sloping bed and open symbols for flat bed. Circular red markers:
![]() $k_{f}R=0.188$
; square blue markers:
$k_{f}R=0.188$
; square blue markers:
![]() $k_{f}R=0.246$
; diamond green markers:
$k_{f}R=0.246$
; diamond green markers:
![]() $k_{f}R=0.373$
; triangle black markers:
$k_{f}R=0.373$
; triangle black markers:
![]() $k_{f}R=0.753$
.
$k_{f}R=0.753$
.

Figure 25. Variation of the phases of the fifth-order harmonic forces with wave steepness
![]() $k_{f}A_{f}$
. Solid symbols for sloping bed tests and open symbols for flat bed cases. Circular red markers:
$k_{f}A_{f}$
. Solid symbols for sloping bed tests and open symbols for flat bed cases. Circular red markers:
![]() $k_{f}R=0.188$
; square blue markers:
$k_{f}R=0.188$
; square blue markers:
![]() $k_{f}R=0.246$
; diamond green markers:
$k_{f}R=0.246$
; diamond green markers:
![]() $k_{f}R=0.373$
; triangle black markers:
$k_{f}R=0.373$
; triangle black markers:
![]() $k_{f}R=0.753$
.
$k_{f}R=0.753$
.
7.2 General reconstruction of forces
We aim to reconstruct the total force time history in terms of the linear component, an amplitude coefficient and phase for each harmonic (3.5). Now we use values for the averaged coefficients in table 2 in the Appendix. As an example we take cases with
![]() $f_{p}=0.82~\text{Hz}$
(
$f_{p}=0.82~\text{Hz}$
(
![]() $k_{f}R=0.373/k_{f}d_{f}=1.51$
) for both sloping and flat bed tests. It can be seen from the figures and the table that
$k_{f}R=0.373/k_{f}d_{f}=1.51$
) for both sloping and flat bed tests. It can be seen from the figures and the table that
![]() $S_{FE1}=5.617$
,
$S_{FE1}=5.617$
,
![]() $S_{FE2}=0.95$
,
$S_{FE2}=0.95$
,
![]() $S_{FE3}=0.87$
,
$S_{FE3}=0.87$
,
![]() $S_{FE4}=0.67$
and
$S_{FE4}=0.67$
and
![]() $S_{FE5}=0.70$
, respectively, for all the
$S_{FE5}=0.70$
, respectively, for all the
![]() $k_{f}A_{f}$
considered in this paper. In terms of phase angles,
$k_{f}A_{f}$
considered in this paper. In terms of phase angles,
![]() $\unicode[STIX]{x1D719}_{2}=103^{\circ }$
(1.80 rad),
$\unicode[STIX]{x1D719}_{2}=103^{\circ }$
(1.80 rad),
![]() $\unicode[STIX]{x1D719}_{3}=76^{\circ }$
(1.33 rad),
$\unicode[STIX]{x1D719}_{3}=76^{\circ }$
(1.33 rad),
![]() $\unicode[STIX]{x1D719}_{4}=208^{\circ }$
(3.63 rad) and
$\unicode[STIX]{x1D719}_{4}=208^{\circ }$
(3.63 rad) and
![]() $\unicode[STIX]{x1D719}_{5}=250^{\circ }$
(4.36 rad). Figure 26 shows the force reconstruction results for flat bed cases, with
$\unicode[STIX]{x1D719}_{5}=250^{\circ }$
(4.36 rad). Figure 26 shows the force reconstruction results for flat bed cases, with
![]() $A_{f}=0.041$
and
$A_{f}=0.041$
and
![]() $A_{f}=0.075$
(
$A_{f}=0.075$
(
![]() $k_{f}A_{f}=0.122$
and
$k_{f}A_{f}=0.122$
and
![]() $k_{f}A_{f}=0.224$
). Similar results for sloping bed cases are shown in figure 27. Note that the envelopes of the measured linear component are used for the reconstruction. It can be seen from the figures that the reconstructed harmonics match as well as those shown in figure 12 for the extracted harmonics, confirming that the proposed reconstruction method is robust and the harmonic structure of the wave loading on the cylinder is independent of bed slope and wave steepness if the Huseby and Grue’s scaling for force is applied. It can be seen that the fifth harmonic is out of position by 1 s for the smaller wave steepness on both flat and sloping beds; we have no explanation for this.
$k_{f}A_{f}=0.224$
). Similar results for sloping bed cases are shown in figure 27. Note that the envelopes of the measured linear component are used for the reconstruction. It can be seen from the figures that the reconstructed harmonics match as well as those shown in figure 12 for the extracted harmonics, confirming that the proposed reconstruction method is robust and the harmonic structure of the wave loading on the cylinder is independent of bed slope and wave steepness if the Huseby and Grue’s scaling for force is applied. It can be seen that the fifth harmonic is out of position by 1 s for the smaller wave steepness on both flat and sloping beds; we have no explanation for this.
This reconstruction method could be applied for practical engineering analysis as the linear component can be accurately approximated by either the Morison equation or classical linear diffraction theory very simply.

Figure 26. The reconstruction of horizontal wave loading on the cylinder and the envelopes for both focused wave groups with
![]() $A_{f}=0.041~\text{m}$
and 0.075 m propagating in a flat bed using the force coefficients and phase angles shown in figures 14–22. The peak frequency
$A_{f}=0.041~\text{m}$
and 0.075 m propagating in a flat bed using the force coefficients and phase angles shown in figures 14–22. The peak frequency
![]() $f_{p}=0.82~\text{Hz}$
. (a)
$f_{p}=0.82~\text{Hz}$
. (a)
![]() $A_{f}=0.041~\text{m}$
,
$A_{f}=0.041~\text{m}$
,
![]() $k_{f}A_{f}=0.122$
, (b)
$k_{f}A_{f}=0.122$
, (b)
![]() $A_{f}=0.075~\text{m}$
,
$A_{f}=0.075~\text{m}$
,
![]() $k_{f}A_{f}=0.224$
.
$k_{f}A_{f}=0.224$
.

Figure 27. The reconstruction of horizontal wave loading on the cylinder and the envelopes for both focused wave groups with
![]() $A_{f}=0.049~\text{m}$
and 0.079 m propagating in a sloping bed using the force coefficients and phase angles shown in figures 14–22. The peak frequency
$A_{f}=0.049~\text{m}$
and 0.079 m propagating in a sloping bed using the force coefficients and phase angles shown in figures 14–22. The peak frequency
![]() $f_{p}=0.82~\text{Hz}$
. (a)
$f_{p}=0.82~\text{Hz}$
. (a)
![]() $A_{f}=0.049~\text{m}$
,
$A_{f}=0.049~\text{m}$
,
![]() $k_{f}A_{f}=0.146$
, (b)
$k_{f}A_{f}=0.146$
, (b)
![]() $A_{f}=0.079~\text{m}$
,
$A_{f}=0.079~\text{m}$
,
![]() $k_{f}A_{f}=0.237$
.
$k_{f}A_{f}=0.237$
.
8 The harmonic structure of the hydrodynamic force as a function of a linear force component
In § 7, we demonstrated that the linear and second-order sum contributions to force can be well approximated using the linear input wave elevation time history in the undisturbed field at the position of the loaded column. Now, we go one stage further and create a nonlinear harmonic force model based only on the linear force time history. We find that this works as well as the
![]() $\unicode[STIX]{x1D702}$
-based reconstructions for the force harmonics. It shows the same localization of harmonics in time and the same type of amplitude scaling as the
$\unicode[STIX]{x1D702}$
-based reconstructions for the force harmonics. It shows the same localization of harmonics in time and the same type of amplitude scaling as the
![]() $\unicode[STIX]{x1D702}$
-based model. But it requires only force information rather than force and elevation. We define a Huseby and Grue scaling for the force harmonic in terms of the linear force equivalent to this one in terms of wave amplitude.
$\unicode[STIX]{x1D702}$
-based model. But it requires only force information rather than force and elevation. We define a Huseby and Grue scaling for the force harmonic in terms of the linear force equivalent to this one in terms of wave amplitude.
Another check on the Stokes-like amplitude scaling is carried out based on a modified Huseby and Grue scaling, but now without reference to the input wave amplitude. The results equivalent to figure 13 are shown in figure 28. The amplitude of the envelope of the
![]() $n$
th harmonic force is non-dimensionalized dividing by
$n$
th harmonic force is non-dimensionalized dividing by
![]() $(\unicode[STIX]{x1D70C}gR^{3})^{(1-n)}{\mathcal{F}}_{1}^{n}$
.
$(\unicode[STIX]{x1D70C}gR^{3})^{(1-n)}{\mathcal{F}}_{1}^{n}$
.
![]() ${\mathcal{F}}_{1}$
is the peak of the envelope of the linear force component. It can be seen from figures that the Stokes scaling applies quite well in these cases, with close matching in wave shapes and sizes of each harmonic. Again, the slight difference in the third-order harmonic force is observed.
${\mathcal{F}}_{1}$
is the peak of the envelope of the linear force component. It can be seen from figures that the Stokes scaling applies quite well in these cases, with close matching in wave shapes and sizes of each harmonic. Again, the slight difference in the third-order harmonic force is observed.

Figure 28. The harmonic structures of horizontal wave loading on the cylinder and the envelopes for both focused wave groups with
![]() $A_{f}=0.096~\text{m}$
and 0.111 m propagating in a sloping bed. The peak frequency
$A_{f}=0.096~\text{m}$
and 0.111 m propagating in a sloping bed. The peak frequency
![]() $f_{p}=0.49~\text{Hz}$
. (a)
$f_{p}=0.49~\text{Hz}$
. (a)
![]() $A_{f}=0.096~\text{m}$
(
$A_{f}=0.096~\text{m}$
(
![]() $k_{f}A_{f}=0.144$
): (b)
$k_{f}A_{f}=0.144$
): (b)
![]() $A_{f}=0.111~\text{m}$
(
$A_{f}=0.111~\text{m}$
(
![]() $k_{f}A_{f}=0.167$
).
$k_{f}A_{f}=0.167$
).
9 Conclusions
A series of experiments have been carried out in this study to investigate the nonlinear forces on a model of an offshore wind turbine foundation, represented by a bottom-mounted vertical piercing cylinder, for a range of wave conditions. Focused wave groups consistent with a JONSWAP spectral form (with a peak spectral frequency of
![]() $f_{p}$
) were applied to model a localized large wave in the laboratory. The use of wave groups overcomes the shortcomings of regular waves, which lack proper representation of the broadband spectrum of real ocean waves. Their implementation in the laboratory testing is efficient, with both the amplitude and phase of the spectral components being carefully controlled. Nonlinearity in the incident waves and in the wave–structure interactions generates higher harmonic forces at frequencies that are approximately integer multiples of the input spectral peak frequencies
$f_{p}$
) were applied to model a localized large wave in the laboratory. The use of wave groups overcomes the shortcomings of regular waves, which lack proper representation of the broadband spectrum of real ocean waves. Their implementation in the laboratory testing is efficient, with both the amplitude and phase of the spectral components being carefully controlled. Nonlinearity in the incident waves and in the wave–structure interactions generates higher harmonic forces at frequencies that are approximately integer multiples of the input spectral peak frequencies
![]() $f_{p}$
. These high-frequency wave-induced loads could be significant enough to cause ‘ringing’, which is a transient violent dynamic response of the structure due to resonant excitation in the lightly damped system. Thus, this study has concentrated on the extraction of the complete harmonic structure of the wave loads rather than on the ‘ringing’ response of the structure itself.
$f_{p}$
. These high-frequency wave-induced loads could be significant enough to cause ‘ringing’, which is a transient violent dynamic response of the structure due to resonant excitation in the lightly damped system. Thus, this study has concentrated on the extraction of the complete harmonic structure of the wave loads rather than on the ‘ringing’ response of the structure itself.
Tests for crest focused wave groups and the same wave group inverted were carried out in pairs in order to apply the ‘phase-inversion’ method to decompose the total hydrodynamic force into its fundamental harmonics. The total hydrodynamic force is separated into odd and even harmonics by linear combinations of resultant force time histories for the crest and trough signals. To ensure that the odd and even harmonics are completely separated, the crest and trough signals have to be aligned in time. The cross-correlation between the signals is used to obtain the optimal alignment and hence the minimum ‘leakage’ from the odd harmonics into assumed even spectra components and vice versa. The complete harmonic structure can then be obtained by digital band-pass filtering. In this study, a band-pass filter with a range of
![]() $f_{p}$
centred about
$f_{p}$
centred about
![]() $nf_{p}$
is applied. A Hilbert transform is applied here to obtain the envelope of the linear components.
$nf_{p}$
is applied. A Hilbert transform is applied here to obtain the envelope of the linear components.
Remarkably, even for violent nearly breaking waves such as bidirectional crossing wave pairs, the ‘phase-inversion’ method is found to work well. The extracted harmonic structure of the extreme load is still apparent and consistent with that for smaller non-breaking waves. It is also found that the
![]() $n$
th-harmonic force scales with the
$n$
th-harmonic force scales with the
![]() $n$
th power of the envelope of both the linear undisturbed free-surface elevation and the linear force component in both time variation and amplitude. This allows estimation of the higher-order harmonic shapes from knowledge of the linear component alone, and those approximated envelopes can then be used to predict the envelopes at each harmonic for an incident wave group with the same peak spectral frequency and an arbitrary amplitude. Moreover, the actual time history at a higher-order harmonic can be reconstructed to a reasonable approximation from the linear component time history, using an amplitude coefficient and a phase angle at each harmonic. Either the linear surface elevation time history in the undisturbed field at the position of the loaded column or the linear force time history can be used. This work is a generalization of the Stokes-wave perturbation expansion to cylinder loads arising from wave groups. It relies on phase decomposition (here, inverting the paddle signal), so the methodology is not directly applicable to the analysis of loads produced by random wave fields, either in the open sea or in random tank tests.
$n$
th power of the envelope of both the linear undisturbed free-surface elevation and the linear force component in both time variation and amplitude. This allows estimation of the higher-order harmonic shapes from knowledge of the linear component alone, and those approximated envelopes can then be used to predict the envelopes at each harmonic for an incident wave group with the same peak spectral frequency and an arbitrary amplitude. Moreover, the actual time history at a higher-order harmonic can be reconstructed to a reasonable approximation from the linear component time history, using an amplitude coefficient and a phase angle at each harmonic. Either the linear surface elevation time history in the undisturbed field at the position of the loaded column or the linear force time history can be used. This work is a generalization of the Stokes-wave perturbation expansion to cylinder loads arising from wave groups. It relies on phase decomposition (here, inverting the paddle signal), so the methodology is not directly applicable to the analysis of loads produced by random wave fields, either in the open sea or in random tank tests.
In addition to the tests over a flat bed, tests were also performed with a sloping 1-in-20 bed. Comparisons between these indicate that the harmonic wave loading on the cylinder depends only on the wave properties of the local water depth at the centre of the cylinder and not on the relatively mild slope, and hence not directly on the wave properties at the paddle. Further investigation on the effect of wave nonlinearity on the wave loading shows that the total hydrodynamic force increases with increasing wave steepness and decreasing cylinder size. It is also found that the relative contribution from the fundamental force decreases with increasing wave steepness measured at the centre of the cylinder, while the contributions from the higher-order harmonics increase. For certain wave cases, linear loading is less than 40 % of the total wave loading, with higher-order harmonics contributing more than 60 %. This demonstrates the importance of the higher-order nonlinear wave loading on marine structures and the need to consider nonlinear high-order components in the design of such structures.
At the second order and above the harmonic structure is shown to be closely related to the appropriate power of the linear input group. The
![]() $n$
th-harmonic force is non-dimensionalized using the Huseby & Grue (Reference Huseby and Grue2000) scaling, dividing by
$n$
th-harmonic force is non-dimensionalized using the Huseby & Grue (Reference Huseby and Grue2000) scaling, dividing by
![]() $\unicode[STIX]{x1D70C}gA_{f}^{n}R^{(3-n)}$
, which works very well. The linear and the second-order non-dimensional force components are shown to be in excellent agreement with classical diffraction theory based on coefficients evaluated at a frequency corresponding to the peak energy density in the incoming wave. Experimentally, the third-order coefficients are observed to be close to independent of wave steepness but affected by the size of the cylinder, other than for the longest wave conditions (equivalent to the most slender cylinder) where for small wave steepness (
$\unicode[STIX]{x1D70C}gA_{f}^{n}R^{(3-n)}$
, which works very well. The linear and the second-order non-dimensional force components are shown to be in excellent agreement with classical diffraction theory based on coefficients evaluated at a frequency corresponding to the peak energy density in the incoming wave. Experimentally, the third-order coefficients are observed to be close to independent of wave steepness but affected by the size of the cylinder, other than for the longest wave conditions (equivalent to the most slender cylinder) where for small wave steepness (
![]() $k_{f}A_{f}<0.15$
) there seems to be a downward trend with wave steepness, in agreement with the observations of Huseby & Grue (Reference Huseby and Grue2000) at comparable wave steepness and cylinder size but for deeper waters. The force structure is close to identical in the experiments for both sloping and flat bed cases. These experiments confirm as well as extend the results obtained by Huseby & Grue (Reference Huseby and Grue2000) from their experiments on the interaction of regular waves with a vertical cylinder, where the incident wave steepness and cylinder sizes were in the similar range but the water was substantially deeper. The phases of higher-harmonic forces up to fifth order are roughly constant for all wave steepness considered. Generally, the analysis method works best for circumstances when the water depth is larger than
$k_{f}A_{f}<0.15$
) there seems to be a downward trend with wave steepness, in agreement with the observations of Huseby & Grue (Reference Huseby and Grue2000) at comparable wave steepness and cylinder size but for deeper waters. The force structure is close to identical in the experiments for both sloping and flat bed cases. These experiments confirm as well as extend the results obtained by Huseby & Grue (Reference Huseby and Grue2000) from their experiments on the interaction of regular waves with a vertical cylinder, where the incident wave steepness and cylinder sizes were in the similar range but the water was substantially deeper. The phases of higher-harmonic forces up to fifth order are roughly constant for all wave steepness considered. Generally, the analysis method works best for circumstances when the water depth is larger than
![]() $k_{f}d_{f}\sim 0.8$
, the cylinder size is smaller than
$k_{f}d_{f}\sim 0.8$
, the cylinder size is smaller than
![]() $k_{f}R\sim 0.5$
and the wave is non-breaking.
$k_{f}R\sim 0.5$
and the wave is non-breaking.
Acknowledgements
The first author acknowledges the financial support of the University of Bath (grant nos 3451 and 3708) for her PhD study. The project was also supported by EPSRC (project EP/J010316/1 Supergen MARine TechnologY challenge). We thank J. Kirkegaard and all the staff at DHI for their help and hospitality during the experiments, which have been supported by European Community’s Sixth Framework Programme through the Integrated Infrastructure Initiative HYDRALAB III within the Transnational Access Activities, contract no. 022441.
Appendix. The averaged coefficients for all four cylinder sizes
Table 2. The averaged coefficients for all four cylinder sizes.

The averaged coefficient values across all experimental wave steepness above
![]() $kA\sim 0.05$
obtained from figures 15–25 are summarized in table 2. A comment on the reliability of the value or range where it is approximately constant is also included. It can be seen that the analysis method applied in this study works well in general for cases with intermediate water depth and cylinder size (
$kA\sim 0.05$
obtained from figures 15–25 are summarized in table 2. A comment on the reliability of the value or range where it is approximately constant is also included. It can be seen that the analysis method applied in this study works well in general for cases with intermediate water depth and cylinder size (
![]() $k_{f}d_{f}>0.8$
and
$k_{f}d_{f}>0.8$
and
![]() $k_{f}R<0.5$
).
$k_{f}R<0.5$
).





































