Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-23T18:02:44.185Z Has data issue: false hasContentIssue false
  • English
  • Français

Yield-stress fluid deposition in circular channels

Published online by Cambridge University Press:  06 April 2017

Benoît Laborie Open the ORCID record for Benoît Laborie [Opens in a new window] ,
Florence Rouyer ,
Dan E. Angelescu  and
Elise Lorenceau
Benoît Laborie*
Affiliation:
Université Paris-Est, Laboratoire Navier, UMR 8205 CNRS, ENPC ParisTech, IFSTTAR, 2 allée Kepler, 77 420 Champs-Sur-Marne, France Université Paris-Est, ESIEE Paris/ESYCOM, 2 Bd. Blaise Pascal, 93162 Noisy le Grand, France
Florence Rouyer
Affiliation:
Université Paris-Est, Laboratoire Navier, UMR 8205 CNRS, ENPC ParisTech, IFSTTAR, 5 Bd. Descartes 77 454 Champs-Sur-Marne, France
Dan E. Angelescu
Affiliation:
Université Paris-Est, ESIEE Paris/ESYCOM, 2 Bd. Blaise Pascal, 93162 Noisy le Grand, France Fluidion SAS, 231 Rue St. Honoré, 75001 Paris, France
Elise Lorenceau
Affiliation:
Université Paris-Est, Laboratoire Navier, UMR 8205 CNRS, ENPC ParisTech, IFSTTAR, 2 allée Kepler, 77 420 Champs-Sur-Marne, France
*
†Email address for correspondence: blaborie@lps.ens.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Since the pioneering works of Taylor and Bretherton, the thickness 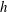$h$ of the film deposited behind a long bubble invading a Newtonian fluid is known to increase with the capillary number power 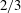$2/3$ (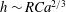$h\sim RCa^{2/3}$), where 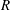$R$ is the radius of the circular tube and 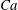$Ca$ is the capillary number, comparing the viscous and capillary effects. This law, known as Bretherton’s law, is valid only in the limit of 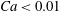$Ca<0.01$ and negligible inertia and gravity. We revisit this classical problem when the fluid is a yield-stress fluid (YSF) exhibiting both a yield stress and a shear-thinning behaviour. First, we provide quantitative measurement of the thickness of the deposited layer for Carbopol, a Herschel–Bulkley fluid, in the limit where the yield stress is of a similar order of magnitude to the capillary pressure and for 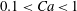$0.1<Ca<1$. To understand our observations, we use scaling arguments to extend the analytical expression of Bretherton’s law to YSFs in circular tubes. In the limit of 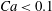$Ca<0.1$, our scaling law, in which the adjustable parameters are set using previous results concerning non-Newtonian fluids, successfully retrieves several features of the literature. First, it shows that (i) the thickness deposited behind a Bingham YSF (exhibiting a yield stress only) is larger than for a Newtonian fluid and (ii) the deposited layer increases with the amplitude of the yield stress. This is in quantitative agreement with previous numerical results concerning Bingham fluids. It also agrees with results concerning pure shear-thinning fluids in the absence of yield stress: the shear-thinning behaviour of the fluid reduces the deposited thickness as previously observed. Last, in the limit of vanishing velocity, our scaling law predicts that the thickness of the deposited YSF converges towards a finite value, which presumably depends on the microstructure of the YSF, in agreement with previous research on the topic performed in different geometries. For 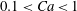$0.1<Ca<1$, the scaling law fails to describe the data. In this limit, nonlinear effects must be taken into account.

JFM classification

Drops and Bubbles: Bubble dynamics Materials Processing Flows: Coating Non-Newtonian Flows: Non-Newtonian Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 818 , 10 May 2017 , pp. 838 - 851
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashmore, J., Shen, A. Q., Kavehpour, H. P., Stone, H. A. & McKinley, G. H. 2008 Coating flows of non-Newtonian fluids: weakly and strongly elastic limits. J. Engng Maths 60, 17–41.Google Scholar
Aussillous, P. & Quéré, D. 2000 Quick deposition of a fluid on the wall of a tube. Phys. Fluids 12, 2367–2371.CrossRefGoogle Scholar
Barnes, H. A. 1995 A review of the slip (wall depletion) of polymer solutions, emulsions and particle suspensions in viscometers: its cause, character, and cure. J. Fluid Mech. 56, 221–251.Google Scholar
Baudoin, M., Song, Y., Manneville, P. & Baroud, C. N. 2013 Airway reopening through catastrophic events in a hierarchical network. Proc. Natl Acad. Sci. USA 110 (3), 859–864.Google Scholar
Behr, M., Arora, D., Coronado, O. M. & M., Pasquali 2005 Gls-type finite element methods for visco-elastic fluid flow simulations. In Proceedings of the third MIT Conference on Computational Fluid and Solid Mechanics, pp. 586–589.Google Scholar
Boehm, M. W., Sarker, S. & Koelling, K. 2011 An experimental investigation of two-phase coating flow within microchannels: the effect of coating fluid rheology. Microfluid. Nanofluid. 10 (6), 1175–1183.Google Scholar
Boronin, S. A., Osiptsov, A. A. & Desroches, J. 2015 Displacement of yield-stress fluids in a fracture. Intl J. Multiphase Flow 76, 47–63.Google Scholar
Boujlel, J. & Coussot, P. 2013 Measuring the surface tension of yield-stress fluids. Soft Matt. 9, 5898–5908.Google Scholar
Bretherton, F. P. 1961 The motion of long bubbles in tubes. J. Fluid Mech. 10, 166–188.CrossRefGoogle Scholar
Coussot, P., Tocquer, L., Lanos, C. & Ovarlez, G. 2009 Macroscopic versus local rheology of yield stress fluids. J. Fluid Mech. 158, 85–90.Google Scholar
Cox, B. G. 1962 On driving a viscous fluid out of a tube. J. Fluid Mech. 14, 81–96.CrossRefGoogle Scholar
Deryagin, B. V. & Levi, S. M. 1964 Film Coating Theory. The Focal Press.Google Scholar
Duggal, R. & Pasquali, M. 2004 Visualization of individual DNA molecules in a small-scale coating flow. J. Rheol. 48, 745–764.Google Scholar
Froishteter, G. B. & Vinogradov, G. V. 1980 The laminar flow of plastic disperse systems in circular tubes. Rheol. Acta 19 (2), 239–250.Google Scholar
Fujioka, H., Takayama, S. & Grotberg, J. B. 2008 Unsteady propagation of a liquid plug in a liquid-lined straight tube. Phys. Fluids 20, 062104.Google Scholar
Gauri, V. & Koelling, K. W. 1999 The motion of long bubbles through viscoelastic fluids in capillary tubes. Rheol. Acta 38, 458–470.Google Scholar
Gutfinger, C. & Tallmadge, J. A. 1965 Films of non-Newtonian fluids adhering to flat plates. AIChE J. 11 (3), 403–413.Google Scholar
Hewson, R. W., Kapur, N. & Gaskell, P. H. 2009 A model for film-forming with Newtonian and shear-thinning fluids. J. Fluid Mech. 162, 21–28.Google Scholar
Huzyak, P. C. & Koelling, K. W. 1997 The penetration of a long bubble through a viscoelastic fluid in a tube. J. Fluid Mech. 71, 73–88.Google Scholar
Jalaal, M. & Balmforth, N. J. 2016 Long bubbles in tubes filled with viscoplastic fluid. J. Non-Newtonian Fluid Mech 238, 100–106.Google Scholar
Jorgensen, L., Le Merrer, M., Delanoe-Ayari, H. & Barentin, C. 2015 Yield stress and elasticity influence on surface tension measurements. Soft Matt. 11, 5111–5121.Google Scholar
Kamışlı, F. 2003 Free coating of a non-Newtonian liquid onto walls of a vertical and inclined tube. Chem. Engng Process. 42 (7), 569–581.CrossRefGoogle Scholar
Kamisli, F. & Ryan, M. E. 1999 Perturbation method in gas-assisted power-law fluid displacement in a circular tube and a rectangular channel. Chem. Engng J. 75, 167–176.Google Scholar
Kamisli, F. & Ryan, M. E. 2001 Gas-assisted non-Newtonian fluid displacement in circular tubes and noncircular channels. Chem. Engng Sci. 56, 4913–4928.Google Scholar
Landau, L. & Levich, B. 1942 Dragging of a liquid by a moving plate. ACTA Physicochim. USSR 17, 42–54.Google Scholar
Macosko, C. W. 1994 Rheology: Principles, Measurements, and Applications. Wiley-VCH.Google Scholar
Mahaut, F., Chateau, X., Coussot, P. & Ovarlez, G. 2008 Yield stress and elastic modulus of suspensions of noncolloidal particles in yield stress fluids. J. Rheol. 52 (1), 287–313.Google Scholar
Maillard, M., Boujlel, J. & Coussot, P. 2014 Solid-solid transition in landau-levich flow with soft-jammed systems. Phys. Rev. Lett. 112, 068304.Google Scholar
Metivier, C., Rharbi, Y., Magnin, A. & Bou Abboud, A. 2012 Stick-slip control of the carbopol microgels on polymethyl methacrylate transparent smooth walls. Soft Matt. 8, 7365–7367.Google Scholar
Park, C.-S., Baek, S.-Y., Lee, K.-J. & Kim, S. W. 2003 Two-phase flow in a gas-injected capillary tube. Adv. Polym. Tech. 22 (4), 320–328.Google Scholar
Piau, J. M. 2007 Carbopol gels: elastoviscoplastic and slippery glasses made of individual swollen sponges: meso- and macroscopic properties, constitutive equations and scaling laws. J. Fluid Mech. 144, 1–29.Google Scholar
Quéré, D. 1999 Fluid coating on a fiber. Annu. Rev. Fluid Mech. 31, 347–384.Google Scholar
Quéré, D. & de Ryck, A. 1998 Le mouillage dynamique des fibres. In Annales de Physique, vol. 23, pp. 1–149. EDP Sciences.Google Scholar
Quintella, E. F., Mendes, P. R. Souza & Carvalho, M. S. 2007 Displacement flows of dilute polymer solutions in capillaries. J. Fluid Mech. 147, 117–128.Google Scholar
Reinelt, D. A. & Saffman, P. G. 1985 The penetration of a finger into a viscous fluid in a channel and tube. SIAM J. Sci. Comput. 6 (3), 542–561.CrossRefGoogle Scholar
de Ryck, A. & Quéré, D. 1998 Fluid coating from a polymer solution. Langmuir 14 (7), 1911–1914.Google Scholar
Schwartz, L. W., Princen, H. M. & Kiss, A. D. 1986 On the motion of long bubbles in capillary tubes. J. Fluid Mech. 172, 259–275.CrossRefGoogle Scholar
Taylor, G. I. 1961 Deposition of a viscous fluid on the wall of a tube. J. Fluid Mech. 10, 161–165.Google Scholar
Weinstein, S. J. & Ruschak, K. J. 2004 Coating flows. Annu. Rev. Fluid Mech. 36, 29–53.Google Scholar
Zamankhan, P., Helenbrook, B. T., Takayama, S. & Grotberg, J. B. 2012 Steady motion of Bingham liquid plugs in two-dimensional channels. J. Fluid Mech. 705, 258–279.Google Scholar