Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Aglitskiy, Y.
Karasik, M.
Velikovich, A. L.
Serlin, V.
Weaver, J. L.
Kessler, T. J.
Nikitin, S. P.
Schmitt, A. J.
Obenschain, S. P.
Metzler, N.
and
Oh, J.
2012.
Observed transition from Richtmyer-Meshkov jet formation through feedout oscillations to Rayleigh-Taylor instability in a laser target.
Physics of Plasmas,
Vol. 19,
Issue. 10,
Morris, C L
King, N S P
Kwiatkowski, K
Mariam, F G
Merrill, F E
and
Saunders, A
2013.
Charged particle radiography.
Reports on Progress in Physics,
Vol. 76,
Issue. 4,
p.
046301.
Fung, J.
Harrison, A.K.
Chitanvis, S.
and
Margulies, J.
2013.
Ejecta source and transport modeling in the FLAG hydrocode.
Computers & Fluids,
Vol. 83,
Issue. ,
p.
177.
Durand, O.
and
Soulard, L.
2013.
Power law and exponential ejecta size distributions from the dynamic fragmentation of shock-loaded Cu and Sn metals under melt conditions.
Journal of Applied Physics,
Vol. 114,
Issue. 19,
Shao, Jian-Li
Wang, Pei
He, An-Min
Duan, Su-Qing
and
Qin, Cheng-Sen
2013.
Molecular dynamics study on the failure modes of aluminium under decaying shock loading.
Journal of Applied Physics,
Vol. 113,
Issue. 16,
Mikaelian, Karnig O.
2013.
Shock-induced interface instability in viscous fluids and metals.
Physical Review E,
Vol. 87,
Issue. 3,
Filippini, G.
Bourasseau, E.
Ghoufi, A.
Goujon, F.
and
Malfreyt, P.
2014.
Communication: Slab thickness dependence of the surface tension: Toward a criterion of liquid sheets stability.
The Journal of Chemical Physics,
Vol. 141,
Issue. 8,
López Ortega, A.
Lombardini, M.
Pullin, D. I.
and
Meiron, D. I.
2014.
Numerical simulations of the Richtmyer-Meshkov instability in solid-vacuum interfaces using calibrated plasticity laws.
Physical Review E,
Vol. 89,
Issue. 3,
Liu, Y.
and
Grieves, B.
2014.
Ejecta Production and Transport From a Shocked Sn Coupon.
Journal of Fluids Engineering,
Vol. 136,
Issue. 9,
Margolin, Len G.
and
Andrews, Malcolm J.
2014.
Models for Crenulation of a Converging Shell.
Journal of Fluids Engineering,
Vol. 136,
Issue. 8,
Buttler, W T
Oró, D M
Mariam, F G
Saunders, A
Andrews, M J
Cherne, F J
Hammerberg, J E
Hixson, R S
Monfared, S K
Morris, C
Olson, R T
Preston, D L
Stone, J B
Terrones, G
Tupa, D
and
Vogan-McNeil, W
2014.
Explosively driven two-shockwave tools with applications.
Journal of Physics: Conference Series,
Vol. 500,
Issue. 11,
p.
112014.
Prudhomme, G
Mercier, P
and
Berthe, L
2014.
PDV experiments on shock-loaded particles.
Journal of Physics: Conference Series,
Vol. 500,
Issue. 14,
p.
142027.
de Rességuier, T.
Lescoute, E.
Sollier, A.
Prudhomme, G.
and
Mercier, P.
2014.
Microjetting from grooved surfaces in metallic samples subjected to laser driven shocks.
Journal of Applied Physics,
Vol. 115,
Issue. 4,
Monfared, S. K.
Oró, D. M.
Grover, M.
Hammerberg, J. E.
LaLone, B. M.
Pack, C. L.
Schauer, M. M.
Stevens, G. D.
Stone, J. B.
Turley, W. D.
and
Buttler, W. T.
2014.
Experimental observations on the links between surface perturbation parameters and shock-induced mass ejection.
Journal of Applied Physics,
Vol. 116,
Issue. 6,
Prime, M B
Vaughan, D E
Preston, D L
Buttler, W T
Chen, S R
Oró, D M
and
Pack, C
2014.
Using growth and arrest of Richtmyer-Meshkov instabilities and Lagrangian simulations to study high-rate material strength.
Journal of Physics: Conference Series,
Vol. 500,
Issue. 11,
p.
112051.
Buttler, W. T.
Oró, D. M.
Olson, R. T.
Cherne, F. J.
Hammerberg, J. E.
Hixson, R. S.
Monfared, S. K.
Pack, C. L.
Rigg, P. A.
Stone, J. B.
and
Terrones, G.
2014.
Second shock ejecta measurements with an explosively driven two-shockwave drive.
Journal of Applied Physics,
Vol. 116,
Issue. 10,
Velikovich, A. L.
Herrmann, M.
and
Abarzhi, S. I.
2014.
Perturbation theory and numerical modelling of weakly and moderately nonlinear dynamics of the incompressible Richtmyer–Meshkov instability.
Journal of Fluid Mechanics,
Vol. 751,
Issue. ,
p.
432.
Suponitsky, Victoria
Froese, Aaron
and
Barsky, Sandra
2014.
Richtmyer–Meshkov instability of a liquid–gas interface driven by a cylindrical imploding pressure wave.
Computers & Fluids,
Vol. 89,
Issue. ,
p.
1.
Prudhomme, G
Mercier, P
Berthe, L
Bénier, J
and
Frugier, P-A
2014.
Frontal and tilted PDV probes for measuring velocity history of laser-shock induced calibrated particles.
Journal of Physics: Conference Series,
Vol. 500,
Issue. 14,
p.
142022.
Lund, Hugh M.
and
Dalziel, Stuart B.
2014.
Bursting water balloons.
Journal of Fluid Mechanics,
Vol. 756,
Issue. ,
p.
771.
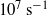 ) and high strains (700 %) as the fundamental link to the onset of ejecta formation. Our experimental observations allow us to approximate the strength of Cu at high strains and strain rates, revealing a unique diagnostic method for use at these extreme conditions.
) and high strains (700 %) as the fundamental link to the onset of ejecta formation. Our experimental observations allow us to approximate the strength of Cu at high strains and strain rates, revealing a unique diagnostic method for use at these extreme conditions.



