Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wong, Jaime G.
Gillespie, Graeme
and
Rival, David E.
2018.
Circulation Redistribution in Leading-Edge Vortices with Spanwise Flow.
AIAA Journal,
Vol. 56,
Issue. 10,
p.
3857.
Menon, Karthik
and
Mittal, Rajat
2019.
Flow physics and dynamics of flow-induced pitch oscillations of an airfoil.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
p.
582.
Su, Yunxing
and
Breuer, Kenneth
2019.
Resonant response and optimal energy harvesting of an elastically mounted pitching and heaving hydrofoil.
Physical Review Fluids,
Vol. 4,
Issue. 6,
Su, Yunxing
Miller, Michael
Mandre, Shreyas
and
Breuer, Kenneth
2019.
Confinement effects on energy harvesting by a heaving and pitching hydrofoil.
Journal of Fluids and Structures,
Vol. 84,
Issue. ,
p.
233.
Bird, Hugh J.
Otomo, Shuji
Ramesh, Kiran Kumar
and
Viola, Ignazio Maria
2019.
A Geometrically Non-Linear Time-Domain Unsteady Lifting-Line Theory.
Werner, Nathaniel H.
Chung, Hojae
Wang, Junshi
Liu, Geng
Cimbala, John M.
Dong, Haibo
and
Cheng, Bo
2019.
Radial planetary vorticity tilting in the leading-edge vortex of revolving wings.
Physics of Fluids,
Vol. 31,
Issue. 4,
Zhu, Yuanhang
Su, Yunxing
and
Breuer, Kenneth
2020.
Nonlinear flow-induced instability of an elastically mounted pitching wing.
Journal of Fluid Mechanics,
Vol. 899,
Issue. ,
Chiereghin, N.
Bull, S.
Cleaver, D. J.
and
Gursul, I.
2020.
Three-dimensionality of leading-edge vortices on high aspect ratio plunging wings.
Physical Review Fluids,
Vol. 5,
Issue. 6,
Zhu, Yuanhang
Su, Yunxing
and
Breuer, Kenneth
2020.
Non-Linear Stability Boundaries of an Elastically-Mounted Pitching Wing.
Ōtomo, Shūji
Henne, Sabrina
Mulleners, Karen
Ramesh, Kiran
and
Viola, Ignazio Maria
2021.
Unsteady lift on a high-amplitude pitching aerofoil.
Experiments in Fluids,
Vol. 62,
Issue. 1,
Xiang, Yang
Hang, Haotian
Qin, Suyang
and
Liu, Hong
2021.
Scaling analysis of the circulation growth of leading-edge vortex in flapping flight.
Acta Mechanica Sinica,
Vol. 37,
Issue. 10,
p.
1530.
Zurman-Nasution, Andhini N.
Ganapathisubramani, Bharathram
and
Weymouth, Gabriel D.
2021.
Fin sweep angle does not determine flapping propulsive performance.
Journal of The Royal Society Interface,
Vol. 18,
Issue. 178,
p.
20210174.
Chen, Qingmin
Hu, Tianxiang
Liu, Peiqing
Qu, Qiulin
Guo, Hao
and
Akkermans, Rinie A.D.
2021.
The dynamic vortical flow behaviour on a coplanar canard configuration during large-amplitude-pitching.
Aerospace Science and Technology,
Vol. 112,
Issue. ,
p.
106553.
Zhu, Yuanhang
Mathai, Varghese
and
Breuer, Kenneth
2021.
Nonlinear fluid damping of elastically mounted pitching wings in quiescent water.
Journal of Fluid Mechanics,
Vol. 923,
Issue. ,
Gehrke, Alexander
and
Mulleners, Karen
2021.
Phenomenology and scaling of optimal flapping wing kinematics.
Bioinspiration & Biomimetics,
Vol. 16,
Issue. 2,
p.
026016.
Hu, Tianxiang
Zhao, Yue
Liu, Peiqing
Qu, Qiulin
Guo, Hao
and
Akkermans, Rinie AD
2021.
Investigation on lift characteristics of a double-delta wing pitching in various reduced frequencies.
Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering,
Vol. 235,
Issue. 14,
p.
2081.
Zhu, Yuanhang
and
Breuer, Kenneth
2022.
Aeroelastic Instability Boundaries of Pitching Swept Wings.
Wabick, Kevin J.
Johnson, Kyle C.
Berdon, Randall L.
Thurow, Brian S.
and
Buchholz, James H.J.
2023.
Transient leading-edge vortex development on a wing rolling in uniform flow.
Journal of Fluid Mechanics,
Vol. 957,
Issue. ,
Chen, Long
Zhang, Yanlai
Zhou, Chao
and
Wu, Jianghao
2023.
Vorticity dynamics of fully developed leading-edge vortices on revolving wings undergoing pitch-up maneuvers.
Physics of Fluids,
Vol. 35,
Issue. 3,
Paulson, James H.
Jardin, Thierry
and
Buchholz, James H. J.
2023.
Inflow-velocity and rotational effects on revolving and translating wings.
Physics of Fluids,
Vol. 35,
Issue. 11,
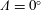 $\unicode[STIX]{x1D6EC}=0^{\circ }$,
$\unicode[STIX]{x1D6EC}=0^{\circ }$, 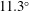 $11.3^{\circ }$,
$11.3^{\circ }$, 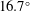 $16.7^{\circ }$) and the reduced frequency (
$16.7^{\circ }$) and the reduced frequency (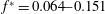 $f^{\ast }=0.064{-}0.151$), while keeping the pitching amplitude and the Reynolds number fixed. Tomographic particle image velocimetry is used to characterise the three-dimensional fluid motion inside the vortex core and its relation to the LEV stability and growth. A series of control volume analyses are performed to quantify the relative importance of the vorticity transport phenomena taking place inside the LEV to the overall vortex development. We show that, near the wing apex where tip effects can be neglected, the vortex develops in a nominally two-dimensional manner, despite the presence of inherently three-dimensional vortex dynamics such as vortex stretching and compression. Furthermore, we demonstrate that the vortex formation time and circulation growth are well-described by the principles of optimal vortex formation number, and that the occurrence of vortex shedding is dictated by the relative energetics of the feeding shear layer and the resulting vortex.
$f^{\ast }=0.064{-}0.151$), while keeping the pitching amplitude and the Reynolds number fixed. Tomographic particle image velocimetry is used to characterise the three-dimensional fluid motion inside the vortex core and its relation to the LEV stability and growth. A series of control volume analyses are performed to quantify the relative importance of the vorticity transport phenomena taking place inside the LEV to the overall vortex development. We show that, near the wing apex where tip effects can be neglected, the vortex develops in a nominally two-dimensional manner, despite the presence of inherently three-dimensional vortex dynamics such as vortex stretching and compression. Furthermore, we demonstrate that the vortex formation time and circulation growth are well-described by the principles of optimal vortex formation number, and that the occurrence of vortex shedding is dictated by the relative energetics of the feeding shear layer and the resulting vortex.




