Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang, Cheng
Jiang, Lin-feng
Jiang, He-chuan
Sun, Chao
and
Liu, Shuang
2021.
Heat transfer and flow structure of two-dimensional thermal convection over ratchet surfaces.
Journal of Hydrodynamics,
Vol. 33,
Issue. 5,
p.
970.
Yang, Tianyong
Wang, Bofu
Wu, Jianzhao
Lu, Zhiming
and
Zhou, Quan
2021.
Horizontal convection in a rectangular enclosure driven by a linear temperature profile.
Applied Mathematics and Mechanics,
Vol. 42,
Issue. 8,
p.
1183.
Fan, Yifan
Zhao, Yongling
Torres, Juan F.
Xu, Feng
Lei, Chengwang
Li, Yuguo
and
Carmeliet, Jan
2021.
Natural convection over vertical and horizontal heated flat surfaces: A review of recent progress focusing on underpinnings and implications for heat transfer and environmental applications.
Physics of Fluids,
Vol. 33,
Issue. 10,
Pandey, Ambrish
Schumacher, Jörg
and
Sreenivasan, Katepalli R.
2021.
Non-Boussinesq convection at low Prandtl numbers relevant to the Sun.
Physical Review Fluids,
Vol. 6,
Issue. 10,
Xia, Shu-Ning
Wu, Jian-Zhao
Wan, Zhen-Hua
Wang, Bo-Fu
Lu, Zhi-Ming
and
Zhou, Quan
2021.
Thermal convection in a tilted rectangular box.
AIP Advances,
Vol. 11,
Issue. 10,
Rodakoviski, Rodrigo
and
Dias, Nelson L.
2021.
Direct simulation of two-dimensional Bénard flow with free-slip boundary conditions.
Computers & Fluids,
Vol. 228,
Issue. ,
p.
105040.
Zhou, Wen-Feng
and
Chen, Jun
2021.
Large-scale structures of turbulent Rayleigh–Bénard convection in a slim-box.
Physics of Fluids,
Vol. 33,
Issue. 6,
Zhao, Chao-Ben
Zhang, Yi-Zhao
Wang, Bo-Fu
Wu, Jian-Zhao
Chong, Kai Leong
and
Zhou, Quan
2022.
Modulation of turbulent Rayleigh-Bénard convection under spatially harmonic heating.
Physical Review E,
Vol. 105,
Issue. 5,
Wu, Jian-Zhao
Wang, Bo-Fu
and
Zhou, Quan
2022.
Massive heat transfer enhancement of Rayleigh-Bénard turbulence over rough surfaces and under horizontal vibration.
Acta Mechanica Sinica,
Vol. 38,
Issue. 2,
Guo, Xin-Qian
Wang, Bo-Fu
Wu, Jian-Zhao
Chong, Kai Leong
and
Zhou, Quan
2022.
Turbulent vertical convection under vertical vibration.
Physics of Fluids,
Vol. 34,
Issue. 5,
Wu, Jian-Zhao
Wang, Bo-Fu
Lu, Zhi-Ming
and
Zhou, Quan
2022.
The heat transfer enhancement by unipolar charge injection in a rectangular Rayleigh–Bénard convection.
AIP Advances,
Vol. 12,
Issue. 1,
Cheng, Hang
Shen, Jie
Zhang, YiZhao
Zhou, Quan
Chong, Kai Leong
Liu, YuLu
and
Lu, ZhiMing
2022.
Lagrangian coherent structures and their heat-transport mechanism in the turbulent Rayleigh-Bénard convection.
Science China Technological Sciences,
Vol. 65,
Issue. 4,
p.
966.
Zhao, Chao-Ben
Wang, Bo-Fu
Wu, Jian-Zhao
Chong, Kai Leong
and
Zhou, Quan
2022.
Suppression of flow reversals via manipulating corner rolls in plane Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 946,
Issue. ,
Yang, Wenwu
Zhang, Yi-Zhao
Wang, Bo-Fu
Dong, Yuhong
and
Zhou, Quan
2022.
Dynamic coupling between carrier and dispersed phases in Rayleigh–Bénard convection laden with inertial isothermal particles.
Journal of Fluid Mechanics,
Vol. 930,
Issue. ,
Cheng, Hang
Jiang, Hao
Chong, Kai Leong
Zhou, Quan
Liu, Yulu
and
Lu, Zhiming
2022.
The effect of surface roughness on the Lagrangian coherent structures in turbulent Rayleigh–Bénard convection.
Physics of Fluids,
Vol. 34,
Issue. 11,
Noormohammadi, Asghar
and
Wang, Bing-Chen
2022.
Study of turbulent dispersion of a concentration plume emitting from a line source over a rib‐roughened surface.
International Journal of Heat and Mass Transfer,
Vol. 195,
Issue. ,
p.
123132.
Sharma, Mukesh
Chand, Krishan
and
De, Arnab Kr.
2022.
Influence of Prandtl number in turbulent Rayleigh-Bénard convection over rough surfaces.
Physical Review Fluids,
Vol. 7,
Issue. 10,
Wu, Jian-zhao
Dong, Dao-liang
Wang, Bo-fu
Dong, Yu-hong
and
Zhou, Quan
2022.
Tuning turbulent convection through rough element arrangement.
Journal of Hydrodynamics,
Vol. 34,
Issue. 2,
p.
308.
Pan, Ming
Dong, Yuhong
Zhou, Quan
and
Shen, Lian
2022.
Flow modulation and heat transport of radiatively heated particles settling in Rayleigh–Bénard convection.
Computers & Fluids,
Vol. 241,
Issue. ,
p.
105454.
Yang, Wenwu
Wan, Zhen-Hua
Zhou, Quan
and
Dong, Yuhong
2022.
On the energy transport and heat transfer efficiency in radiatively heated particle-laden Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 953,
Issue. ,
 $Pr$-dependence of the critical roughness height in two-dimensional turbulent Rayleigh–Bénard convection
$Pr$-dependence of the critical roughness height in two-dimensional turbulent Rayleigh–Bénard convection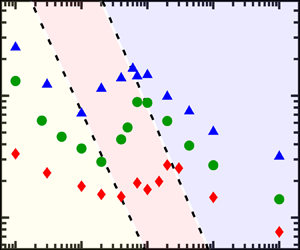
 $10^7\leqslant Ra\leqslant 10^9$ and the Prandtl number range
$10^7\leqslant Ra\leqslant 10^9$ and the Prandtl number range  $0.01\leqslant Pr\leqslant 100$. In Zhang et al. (J. Fluid Mech., vol. 836, 2018, R2), it was reported that while the measured Nusselt number
$0.01\leqslant Pr\leqslant 100$. In Zhang et al. (J. Fluid Mech., vol. 836, 2018, R2), it was reported that while the measured Nusselt number  $Nu$ is enhanced at large roughness height
$Nu$ is enhanced at large roughness height  $h$, the global heat transport is reduced at small
$h$, the global heat transport is reduced at small  $h$. The division between the two regimes yields a critical roughness height
$h$. The division between the two regimes yields a critical roughness height  $h_c$, and we now focus on the effects of the Prandtl number (
$h_c$, and we now focus on the effects of the Prandtl number ( $Pr$) on
$Pr$) on  $h_c$. Based on the variations of
$h_c$. Based on the variations of  $h_c$, we identify three regimes for
$h_c$, we identify three regimes for  $h_c(Pr)$. For low
$h_c(Pr)$. For low  $Pr$, thermal boundary layers become thinner with increasing
$Pr$, thermal boundary layers become thinner with increasing  $Pr$. This makes the boundary layers easier to be disrupted by rough elements, leading to the decrease of
$Pr$. This makes the boundary layers easier to be disrupted by rough elements, leading to the decrease of  $h_c$ with increasing
$h_c$ with increasing  $Pr$. For moderate
$Pr$. For moderate  $Pr$, the corner-flow rolls become much more pronounced and suppress the global heat transport via the competition between the corner-flow rolls and the large-scale circulation (LSC). As a consequence,
$Pr$, the corner-flow rolls become much more pronounced and suppress the global heat transport via the competition between the corner-flow rolls and the large-scale circulation (LSC). As a consequence,  $h_c$ increases with increasing
$h_c$ increases with increasing  $Pr$ due to the intensification of the corner–LSC competition. For high
$Pr$ due to the intensification of the corner–LSC competition. For high  $Pr$, the convective flow transitions to the plume-controlled regime. As the rough elements trigger much stronger and more frequent plume emissions,
$Pr$, the convective flow transitions to the plume-controlled regime. As the rough elements trigger much stronger and more frequent plume emissions,  $h_c$ again decreases with increasing
$h_c$ again decreases with increasing  $Pr$.
$Pr$.




