Hostname: page-component-84b7d79bbc-c654p Total loading time: 0 Render date: 2024-07-28T02:35:28.099Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillatory switching centrifugation: dynamics of a particle in a pulsating vortex

Published online by Cambridge University Press:  25 October 2018

Francesco Romanò Open the ORCID record for Francesco Romanò [Opens in a new window]
Francesco Romanò*
Affiliation:
Department of Biomedical Engineering, University of Michigan, 2123 Carl A. Gerstacker Building, 2200 Bonisteel Boulevard, Ann Arbor, MI 48109-2099, USA
*
†Email address for correspondence: frromano@umich.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamics of a small rigid spherical particle in an unbounded pulsating vortex is considered, keeping constant the particle Stokes number 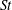$St$ and varying the particle-to-fluid density ratio 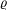$\unicode[STIX]{x1D71A}$ and the pulsation frequency of the vortex 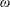$\unicode[STIX]{x1D714}$. We show that the asymptotic dynamics of a particle of given 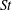$St$ and 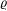$\unicode[STIX]{x1D71A}$ can be controlled by varying 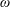$\unicode[STIX]{x1D714}$, turning the vortex core either into an attractor or a repellor. The creation of non-trivial particle limit cycles characterizes the boundaries between centrifugal and centripetal regions in parameter space. The discovered phenomenon is termed oscillatory switching centrifugation and its implications for particle demixing processes, biological protocols, lab-on-a-chip devices and dynamical systems theory are discussed at the end.

JFM classification

Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Multiphase and Particle-laden Flows: Particle/fluid flow Geophysical and Geological Flows: Rotating flows
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 857 , 25 December 2018 , R3
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Babiano, A., Cartwright, J. H. E., Piro, O. & Provenzale, A. 2000 Dynamics of a small neutrally buoyant sphere in a fluid and targeting in Hamiltonian systems. Phys. Rev. Lett. 84, 5764–5767.Google Scholar
Bluemink, J. J., Lohse, D., Prosperetti, A. & Van Wijngaarden, L. 2008 A sphere in a uniformly rotating or shearing flow. J. Fluid Mech. 600, 201233.Google Scholar
Bluemink, J. J., Lohse, D., Prosperetti, A. & Van Wijngaarden, L. 2010 Drag and lift forces on particles in a rotating flow. J. Fluid Mech. 643, 1–31.Google Scholar
Brenner, H. 1961 The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Engng Sci. 16, 242–251.Google Scholar
Candelier, F. 2008 Time-dependent force acting on a particle moving arbitrarily in a rotating flow, at small Reynolds and Taylor numbers. J. Fluid Mech. 608, 319–336.Google Scholar
Candelier, F., Angilella, J.-R. & Souhar, M. 2005 On the effect of inertia and history forces on the slow motion of a spherical solid or gaseous inclusion in a solid-body rotation flow. J. Fluid Mech. 545, 113–139.Google Scholar
Daitche, A. 2013 Advection of inertial particles in the presence of the history force: higher order numerical schemes. J. Comput. Phys. 254, 93–106.Google Scholar
Ducrée, J., Haeberle, S., Lutz, S., Pausch, S., Stetten, F. V. & Zengerle, R. 2007 The centrifugal microfluidic bio-disk platform. J. Micromech. Microengng 17, S103–S115.Google Scholar
Farazmand, M. & Haller, G. 2015 The Maxey–Riley equation: existence, uniqueness and regularity of solutions. Nonlinear Anal. Real 22, 98–106.Google Scholar
Faxén, H. 1922 Der Widerstand gegen die Bewegung einer starren Kugel in einer zähen Flüssigkeit, die zwischen zwei parallelen ebenen Wänden eingeschlossen ist. Ann. Phys. 373, 89–119.Google Scholar
Herron, I. H., Davis, S. H. & Bretherton, F. P. 1975 On the sedimentation of a sphere in a centrifuge. J. Fluid Mech. 68 (2), 209–234.Google Scholar
Hocking, L. M., Moore, D. W. & Walton, I. C. 1979 The drag on a sphere moving axially in a long rotating container. J. Fluid Mech. 90 (4), 781–793.Google Scholar
Karanfilian, S. K. & Kotas, T. J. 1981 Motion of a spherical particle in a liquid rotating as a solid body. Proc. R. Soc. Lond. A 376 (1767), 525–544.Google Scholar
Kynch, G. J. 1952 A theory of sedimentation. Trans. Faraday Soc. 48, 166–176.Google Scholar
Lasheras, J. C. & Tio, K.-K. 1994 Dynamics of a small spherical particle in steady two-dimensional vortex flows. Appl. Mech. Rev. 47, S61–S69.Google Scholar
Mark, D., Haeberle, S., Roth, G., Stetten, F. Von & Zengerle, R. 2010 Microfluidic lab-on-a-chip platforms: requirements, characteristics and applications. In Microfluidics Based Microsystems, pp. 305–376. Springer.Google Scholar
Mason, P. J. 1975 Forces on bodies moving transversely through a rotating fluid. J. Fluid Mech. 71 (3), 577–599.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26, 883–889.Google Scholar
Miyazaki, K. 1995 Dependence of the friction tensor on the rotation of a frame of reference. Physica A 222 (1–4), 248–260.Google Scholar
Romanò, F. & Kuhlmann, H. C. 2017 Particle–boundary interaction in a shear-driven cavity flow. Theor. Comput. Fluid Dyn. 31, 427–445.Google Scholar
Romanò, F. & Kuhlmann, H. C. 2018 Finite-size Lagrangian coherent structures in thermocapillary liquid bridges. Phys. Rev. Fluids 3, 094302.Google Scholar
Sapsis, T. & Haller, G. 2009 Inertial particle dynamics in a hurricane. J. Atmos. Sci. 66, 2481–2492.Google Scholar
Taylor, G. I. 1922 The motion of a sphere in a rotating liquid. Proc. R. Soc. Lond. A 102 (715), 180–189.Google Scholar
Taylor, G. I. 1923 Experiments on the motion of solid bodies in rotating fluids. Proc. R. Soc. Lond. A 104 (725), 213–218.Google Scholar
Weisenborn, A. J. 1985 Drag on a sphere moving slowly in a rotating viscous fluid. J. Fluid Mech. 153, 215–227.Google Scholar
Xu, S. & Nadim, A. 2015 Three models for rectlinear particle motion with the Basset history force. Electron. J. Differ. Equ. 2015 (104), 1–19.Google Scholar
Xu, S. & Nadim, A. 2016 Oscillatory counter-centrifugation. Phys. Fluids 28, 021302.Google Scholar